Codeforces 506E Mr. Kitayuta's Gift (矩阵乘法，动态规划)

描述：

给出一个单词，在单词中插入若干字符使其为回文串，求回文串的个数（|s|<=200,n<=10^9）

这道题超神奇，不可多得的一道好题

首先可以搞出一个dp[l][r][i]表示回文串左边i位匹配到第l位，右边i位匹配到第r位的状态数，可以发现可以用矩阵乘法优化（某人说看到n这么大就一定是矩阵乘法了= =）

但这样一共有|s|^2个节点，时间复杂度无法承受

我们先把状态树画出来：例如add

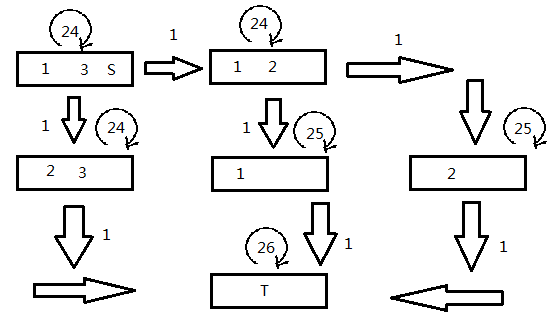可以发现是个DAG

我们考虑把单独的每条链拿出来求解，那么最多会有|s|条不同的链，链长最多为|s|，时间复杂度为O(|s|^4log n)还是得跪

好像没什么思路了对吧= =（我第一步转化就没想到了= =）

我们考虑记有24个自环的为n24，25个自环的为n25，可以发现n24+n25*2=|s|或|s|+1也就是说对于一个确定的n24，一定有一个确定的n25

那么这样构图：

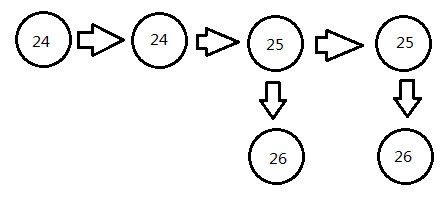可以发现所有状况都被包括进来了！！！

那么一共有2|s|个节点，时间复杂度降了一个|s|，看上去好像还是不行

压常数= =

可以发现这个是棵树，也就是说如果按拓扑序编号的话，到时的矩阵左下角将是什么都没有的

那么就直接for i = 1 to n j = i to n k=i to j 就行了 = =

总结下吧

这道题为何神奇呢

首先它把一个DAG的图拆成了若干条相似的链

然后它又把这些链和成了一个更和谐的图

最后再观察题目性质得到一个比较神奇的优化方法

这给了我们什么启迪呢= =

首先遇到某些DAG我们可以考虑拆成若干条相似的链

遇到某些链我们可以考虑把他们合成一个图

最重要的是，还是得参透题目的性质

这道题基本都是依靠题目的性质到达下一步的，只有真正读懂读透这道题，我们才能想出更好的解法

CODE:

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define maxn 410
#define mod 10007
typedef int ll;
struct marix{
    int r,c;ll a[maxn][maxn];
    inline void init(int x){r=c=x;for (int i=1;i<=x;i++) a[i][i]=1;}
}x,y;
inline void muti(marix &ans,const marix x,const marix y){
    ans.r=ans.c=x.r;
    for (int i=1;i<=x.r;i++) 
        for (int j=i;j<=y.c;j++) {
            int tmp=0;
            for (int k=i;k<=j;k++) 
                (tmp+=x.a[i][k]*y.a[k][j])%=mod;
            ans.a[i][j]=tmp;
        }
}
inline void power(marix &ans,marix x,int y) {
    ans.init(x.r);
    for (;y;y>>=1) {
        if (y&1) muti(ans,ans,x);
        muti(x,x,x);
    }
}
ll f[210][210][210];
char s[maxn];
inline ll calc(int l,int r,int x) {
    ll &u=f[x][l][r];
    if (u!=-1) return u;
    u=0;
    if (l==r) return u=x==0;
    if (s[l]==s[r]) {
        if (l+1==r) return u=x==0;
        return u=calc(l+1,r-1,x);
    }
    if (x>0) return u=(calc(l+1,r,x-1)+calc(l,r-1,x-1))%mod;
    return u;
}
int main(){
    int n,m;
    memset(f,-1,sizeof(f));
    scanf("%s",s+1);
    scanf("%d",&n);
    m=strlen(s+1);
    n+=m;
    int l=(n+1)/2,n24=m-1,n25=(m+1)/2,n26=n25;
    x.r=x.c=n24+n25+n26;
    for (int i=1;i<=n24;i++) x.a[i][i]=24,x.a[i][i+1]=1;
    for (int i=n24+1;i<=n25+n24;i++) x.a[i][i]=25,x.a[i][i+n25]=1;
    for (int i=n24+n25+1;i<=n25+n24+n26;i++) x.a[i][i]=26;
    for (int i=n24+1;i<n25+n24;i++) x.a[i][i+1]=1;
    marix y;
    power(y,x,l-1);
    muti(x,y,x);
    ll ans;
    for (int i=0;i<=n24;i++) {
        int j=(m-i+1)/2,k=l-i-j;
        if (k<0) continue;
        ll sum=calc(1,m,i);
        (ans+=sum*x.a[n24-i+1][n24+j+n25]%mod)%=mod;
        if ((n&1)&&(m-i&1^1)) 
            (ans=ans-sum*y.a[n24-i+1][n24+j]%mod+mod)%=mod;
    }
    printf("%d\n",ans);
    return 0;
}