算法导论————EXKMP
【例题传送门:caioj1461】
【EXKMP】最长共同前缀长度
【题意】
给出模板串A和子串B,长度分别为lenA和lenB,要求在线性时间内,对于每个A[i](1<=i<=lenA),求出A[i..lenA]与B的最长公共前缀长度
【输入文件】
输入A,B两个串,(lenB<=lenA<=1000000)
【输出文件】
输出lenA个数,表示A[i...lenA]与B的最长公共前缀长度,每个数之前有空格
【样例输入】
aabbabaaab
aabb
【样例输出】
4 1 0 0 1 0 2 3 1 0
算法分析:
学EXKMP前,必须将KMP学透,如果仍未学KMP,请出门左转【传送门】
我们在KMP算法中可以理解,p数组是KMP的核心,p[i]代表着以i为结尾和以开头为首的最长公共子串长度,也就是说对于st字符串数组的p[i]代表的就是st字符串数组从1开始到p[i]和从i-p[i]+1到i是完全相同的(st[1...p[i]]=st[i-p[i]+1...i])
那么扩展KMP就高级了。一样还是p数组(还是原来的配方,还是熟悉的味道!),但是既然是扩展KMP就不要用p,我就改成extend数组了,表示的意义与普通KMP就大有不同。extend[i]表示的是以i为首和以开头为首的最长前缀,也就是说对于st字符串数组中的extend[i]表示的就是st字符串数组从1开始到extend[i]和从i到i+extend[i]-1是完全相同的(st[1...extend[i]]=st[i...i+extend[i]-1])
首先extend[1]就不用说了,直接等于len这个没有问题吧,那么因为extend[1]这个是具有一定性,所以我们基本把这东西废掉..那么我们就直接从extend[2]开始。然后我们就定义一个k,这个k表示的就是在当前搜索过的范围以内(因为这是线性算法,所以是从1到len)能到达最远(也就是说k+extend[k]-1最大的)的编号,为什么要定义一个这样子的东西,等下你们就知道了。
我们先定义一个p,让它等于k+extend[k]-1,那么由extend这个数组的定义我们就可以得到一个等式:st[1...extend[k]]=st[k...p]。因为p=k+extend[k]-1,所以我们又可以得到一条等式:extend[k]=p-k+1,把这个代换到上一条等式上,就会——瞬间爆炸!(好吧开个玩笑..)就会变成:st[1...p-k+1]=st[k...p],如下图:
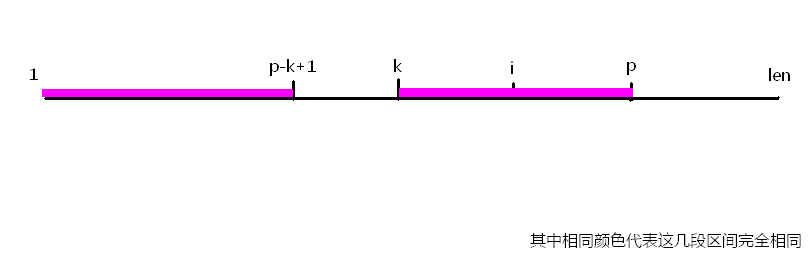
因为我们现在要求从extend[i],那么由上面这条等式又可以得到另一条等式:st[i-k+1...p-k+1]=st[i...p],如下图: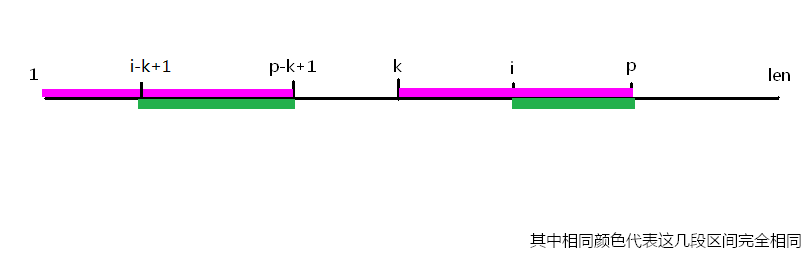
在看此证明过程中请各位一直记住extend数组所表达的含义,不然会有很多地方不懂的。那么我们再定义一个L=extend[i-k+1],我们又可以得到一条等式:st[i-k+1...i-k+L](注意:本来得到的应该是i-k+1+L-1,我直接把+1-1省略了)=st[1...L],如下图:

这个时候有人就会问了:为什么你上面的图不和前几个合在一起呢?这个就是本算法的一个难点了!因为L的不定性,这个时候我们需要考虑i-k+L和p-k+1的大小!那我们就来分开来考虑。
(1)i-k+L<p-k+1,如下图:

从上图我们可以看到因为st[1...L]=st[i-k+1...i-k+L],st[i-k+1...p-k+1]=st[i...p],所以在st[i...p]中肯定含有一段(从i开始)和st[1...L]是完全相同的,也就是上图标出来的蓝色部分st[i...i+L-1]。因为st[i-k+1...p-k+1]=st[i...p]又因为i-k+L<p-k+1,所以我们又可以得到:st[i-k+L+1]=st[i+L](也就是上图所标的黄色位置),而因为extend[i-k+1]的定义,所以st[L+1](也就是上图所标棕色位置)!=st[i-k+L+1],所以我们可以得到:st[i+L]!=st[L+1],那么extend[i]就直接等于L了。
(2)i-k+L>p-k+1,如下图:
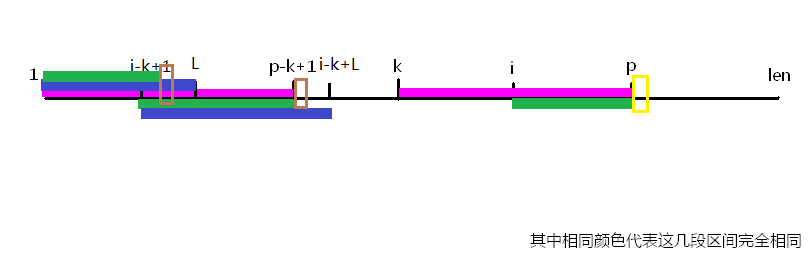
从上图中我们看到因为st[1...L]=st[i-k+1...i-k+L],又因为i-k+L>p-k+1,所以在st[1...L]中肯定含有一段和st[i-k+1...p-k+1]完全相同的(图中绿色部分)。因为extend[k]的意义,所以st[p+1]!=st[p-k+2](图中第二个棕色和黄色位置,为什么不相同不用解释吧),又因为st[1...L]=st[i-k+1...i-k+L],所以st[p-i+2](图中并未标出,第一个棕色位置)=st[p-k+2],那么就会得到:st[p-i+2]!=st[p+1],所以extend[i]就等于p-i+1了。
(3)i-k+L=p-k+1,如下图:
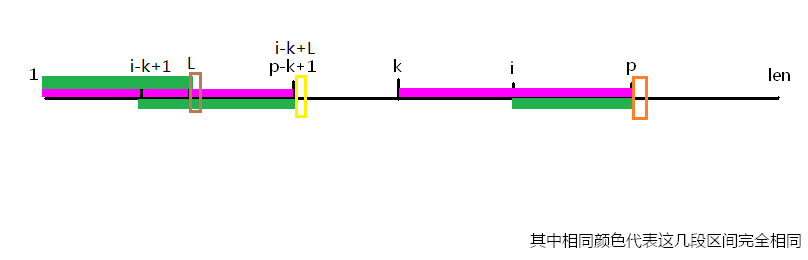
从上图我们可以发现因为st[i-k+1...i-k+L]=st[1..L],st[i-k+1...p-k+1]=st[i...p],又因为i-k+L=p-k+1,所以st[1...L]=st[i-k+1...p-k+1(可换成i-k+L)]=st[i...p](也就是指上图中三段绿色部分)。那么由于extend[i-k+1]和extend[k]的意义表达,我们可以得到:st[L+1]!=st[i-k+L+1],st[i-k+L+1]!=st[p+1],但是我们不能确定st[L+1]和st[p+1]是否相同,我们只能确定从i开始和从1开始有p-i+1这么长的公共前缀但并不一定是最长的(这句话要好好理解,这很重要)。
那么我们就设一个变量j=p-i+1,表示当前从i开始和从1开始的公共前缀长度,由于上面加粗的那句话,我们可以直接从st[j+1]和st[i+j]来累加j的值来得出最长的公共前缀。
注意事项:
因为p是一个不定的数(由k和extend[k]来定),所以说有可能p-i+1是有可能为负数,那么第二种情况显然不对,公共前缀怎么样也不能等于负数吧,最小也会是0吧!这个时候也许你就会冒出一个想法,在第二种情况下取p-i+1和0的最大值。很显然这是不对的。请看下图:

从上图我们可以发现,因为p-i+1是负数,所以上面所有条件都用不了,因为对i后面的字符没有作任何的计算,但这个时候是绝对不可以肯定st[1]和st[i]是不同的(也就是最长公共前缀为0),那么我们需要从st[1]和st[i]开始继续判断后面的字符是否相同。于是我们把第二种情况和第三种情况归纳为一种情况,因为两者都是要暴力处理未知的点,只是起始点不同
这仅仅是求extend数组的证明,也仅仅是在同一个字符串里的基本操作,接下来我就来讲下扩展KMP(简称EXKMP)的实际用途。EXKMP主要是利用于解决处理两个字符串的最长公共前缀长度,假如A是主串,B是副串,那么这时我们定义一个ex数组,ex[i]就表示A[i...Alen]和B[1...Blen]的最长公共前缀长度(这个概念需要好好注意)
其实在处理两者的匹配时,只需要注意将A串中的子串转移到B串中进行处理,那么这样我们实际上在求ex数组时,操作仍与上面的步骤相似
参考代码:
#include<cstdio> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> using namespace std; char sa[1100000],sb[1100000]; int lena,lenb; int p[1100000],ex[1100000]; //p数组是用来让B串自己匹配自己的 void exkmp() { p[1]=lenb; int x=1; while(sb[x]==sb[x+1]&&x+1<=lenb) x++;//因为我们p[1]是具有一定性,所以我们不能直接用,所以要先暴力求出p[2] p[2]=x-1; int k=2; for(int i=3;i<=lenb;i++) { int pp=k+p[k]-1,L=p[i-k+1];//pp实际上是p if(i+L<pp+1) p[i]=L;//i-k+L<pp-k+1化简后i+L<pp else { int j=pp-i+1; if(j<0) j=0; while(sb[j+1]==sb[i+j]&&i+j<=lenb) j++; p[i]=j; k=i; } } x=1; while(sa[x]==sb[x]&&x<=lenb) x++;//ex[1]并不具有一定性,所以我们暴力求出ex[1] ex[1]=x-1; k=1; for(int i=2;i<=lena;i++) { int pp=k+ex[k]-1,L=p[i-k+1]; if(i+L<pp+1) ex[i]=L; else { int j=pp-i+1; if(j<0) j=0; while(sb[j+1]==sa[i+j]&&i+j<=lena&&j<=lenb) j++; ex[i]=j; k=i; } } } int main() { scanf("%s%s",sa+1,sb+1); lena=strlen(sa+1);lenb=strlen(sb+1); exkmp(); for(int i=1;i<lena;i++) printf("%d ",ex[i]); printf("%d\n",ex[lena]); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号