交叉验证 Cross validation
三段论 Why-What-How
- 为什么用交叉验证法?
- 什么是交叉验证法?
- 主要有哪些方法?
- Python代码实例(sklearn)
一、为什么用交叉验证?
The Goal is always to Generalize(泛化)
Test Set 对于未知未来世界的假设,构建模型时绝对不可以动,否则就是Cheating.
统计学家喜欢的数据描述:IID(Independent and identically distributed,独立同分布)
在很多算法中,独立同分布是基本假设。
在数据量不大的情况下,如果不使用交叉验证,只使用一组验证集可能无法代表整个数据集的特点,导致无法获得最佳模型参数。 使用K折交叉验证,通过K次平均可以减少模型评分的统计误差,有利于更好地找到最佳模型参数。
因为在实际的训练中,训练的结果对于训练集的拟合程度通常还是挺好的(初试条件敏感),但是对于训练集之外的数据的拟合程度通常就不那么令人满意了。因此我们通常并不会把所有的数据集都拿来训练,而是分出一部分来(这一部分不参加训练)对训练集生成的参数进行测试,相对客观的判断这些参数对训练集之外的数据的符合程度。
这种思想就称为交叉验证(Cross Validation)
交叉验证意义:
1.交叉验证用于评估模型的预测性能,尤其是训练好的模型在新数据上的表现,可以在一定程度上减小过拟合。
2.可以从有限的数据中获取尽可能多的有效信息。
二、什么是交叉验证法?
它的基本思想就是将训练集(Training Data)进行分组,一部分做为训练集来训练模型,另一部分做为验证集(Validation Data)来评价模型。
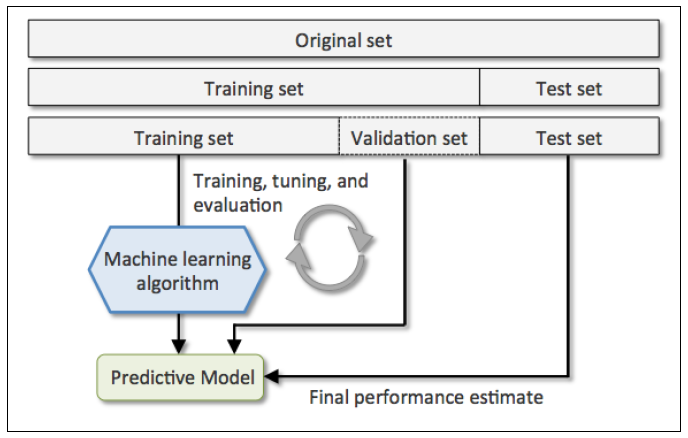
一图顶千字,数据集分类
(测试集 验证集 训练集的比较)
三、交叉验证方法
3.1 留出法 (holdout cross validation)
在机器学习任务中,拿到数据后,我们首先会将原始数据集分为三部分:训练集、验证集和测试集。
训练集用于训练模型,验证集用于模型的参数选择配置,测试集对于模型来说是未知数据,用于评估模型的泛化能力。
这个方法操作简单,只需随机把原始数据分为三组即可。
不过如果只做一次分割,它对训练集、验证集和测试集的样本数比例,还有分割后数据的分布是否和原始数据集的分布相同等因素比较敏感,不同的划分会得到不同的最优模型,而且分成三个集合后,用于训练的数据更少了。
于是就有了 k 折交叉验证(k-fold cross validation) 作为改进。
3.2 k 折交叉验证(k-fold cross validation)
K折交叉验证法将整个训练集分成K组,每次选择其中一组作为验证集(Validation Data),其他K-1组作为训练集(Training Data)。
经过K折交叉验证,一组参数会得到K个评分,将K个评分的平均值作为该组参数的最终评分。

P.S. 图中的Test Fold 即验证集,可以理解为构建模型时使用的伪测试集。
k 折交叉验证通过对 k 个不同分组训练的结果进行平均来减少方差,因此模型的性能对数据的划分就不那么敏感。
- 第一步,不重复抽样将原始数据随机分为 k 份。
- 第二步,每一次挑选其中 1 份作为** 验证测试集 **,剩余 k-1 份作为 训练集用于模型训练。
- 第三步,重复第二步 k 次,这样每个子集都有一次机会作为验证测试集,其余机会作为训练集。
- 在每个训练集上训练后得到一个模型,
- 用这个模型在相应的测试集上测试,计算并保存模型的评估指标,
- 第四步,计算 k 组测试结果的平均值作为模型精度的估计,并作为当前 k 折交叉验证下模型的性能指标。
k 一般取 10,
数据量小的时候,k 可以设大一点,这样训练集占整体比例就比较大,不过同时训练的模型个数也增多。
数据量大的时候,k 可以设小一点。
3.3 留一法(Leave one out cross validation)
当 k=m 即样本总数时,
每次的测试集都只有一个样本,要进行 m 次训练和预测,这就是留一法 。
这个方法用于训练的数据只比整体数据集少了一个样本,因此最接近原始样本的分布。
但是训练复杂度增加了,因为模型的数量与原始数据样本数量相同。
一般在数据缺乏时使用。
此外:
多次 k 折交叉验证再求均值,例如:10 次 10 折交叉验证,以求更精确一点。
划分时有多种方法,例如对非平衡数据可以用分层采样,就是在每一份子集中都保持和原始数据集相同的类别比例。
模型训练过程的所有步骤,包括模型选择,特征选择等都是在单个折叠 fold 中独立执行的。
3.4 Bootstrapping
还有一种比较特殊的交叉验证方式,Bootstrapping: 通过自助采样法,即在含有 m 个样本的数据集中,每次随机挑选一个样本,再放回到数据集中,再随机挑选一个样本,这样有放回地进行抽样 m 次,组成了新的数据集作为训练集。
这里会有重复多次的样本,也会有一次都没有出现的样本,原数据集中大概有 36.8% 的样本不会出现在新组数据集中。
优点是训练集的样本总数和原数据集一样都是 m,并且仍有约 1/3 的数据不被训练而可以作为测试集。
缺点是这样产生的训练集的数据分布和原数据集的不一样了,会引入估计偏差。
此种方法不是很常用,除非数据量真的很少。
四、Python代码实例(sklearn)
4.1 留出法 (holdout cross validation)
下面例子,一共有 150 条数据:
>>> import numpy as np
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import datasets
>>> from sklearn import svm
>>> iris = datasets.load_iris()
>>> iris.data.shape, iris.target.shape
((150, 4), (150,))
用 train_test_split 来随机划分数据集,(test_size = 0.4)
其中 40% 用于测试集,有 60 条数据,60% 为训练集,有 90 条数据:
>>> X_train, X_test, y_train, y_test = train_test_split(
... iris.data, iris.target, test_size=0.4, random_state=0)
>>> X_train.shape, y_train.shape
((90, 4), (90,))
>>> X_test.shape, y_test.shape
((60, 4), (60,))
用 train 来训练,用 test 来评价模型的分数。
>>> clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.96...
4.2 k 折交叉验证(k-fold cross validation)
最简单的方法是直接调用 cross_val_score,这里用了 5 折交叉验证:
>>> from sklearn.model_selection import cross_val_score
>>> clf = svm.SVC(kernel='linear', C=1)
>>> scores = cross_val_score(clf, iris.data, iris.target, cv=5)
>>> scores
array([ 0.96..., 1. ..., 0.96..., 0.96..., 1. ])
得到最后平均分为 0.98,以及它的 95% 置信区间:
>>> print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
Accuracy: 0.98 (+/- 0.03)
我们可以直接看一下 K-fold 是怎样划分数据的:
X 有四个数据,把它分成 2 折,
结果中最后一个集合是测试集,前面的是训练集,
每一行为 1 折:
>>> import numpy as np
>>> from sklearn.model_selection import KFold
>>> X = [0,1, 2, 3]
>>> kf = KFold(n_splits=2)
>>> for train, test in kf.split(X):
... print("%s %s" % (train, test))
[2 3] [0 1]
[0 1] [2 3]
同样的数据 X,我们看 LeaveOneOut 后是什么样子,
那就是把它分成 4 折,
结果中最后一个集合是测试集,只有一个元素,前面的是训练集,
每一行为 1 折:
>>> from sklearn.model_selection import LeaveOneOut
>>> X = [0,1, 2, 3]
>>> loo = LeaveOneOut()
>>> for train, test in loo.split(X):
... print("%s %s" % (train, test))
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号