【Udacity】机器学习性能评估指标
评估指标 Evaluation metrics
机器学习性能评估指标
- 选择合适的指标
- 分类与回归的不同性能指标
- 分类的指标(准确率、精确率、召回率和 F 分数)
- 回归的指标(平均绝对误差和均方误差)
- 混淆矩阵(confusion matricess)
一、选择合适的指标
评估模型是否得到改善,总体表现如何
在构建机器学习模型时,我们首先要选择性能指标,然后测试模型的表现如何。相关的指标有多个,具体取决于我们要尝试解决的问题。
此外,在测试模型时,也务必要将数据集分解为训练数据和测试数据。如果不区分训练数据集和测试数据集,则在评估模型时会遇到问题,因为它已经看到了所有数据。我们需要的是独立的数据集,以确认模型可以很好地泛化,而不只是泛化到训练样本。
二、分类与回归的不同性能指标
分类涉及到根据未见过的样本进行预测,并确定新实例属于哪个类别。例如,可以根据蓝色或红色或者方形或圆形来组织对象,以便在看到新对象时根据其特征来组织对象。
在回归中,我们想根据连续数据来进行预测。例如,我们有包含不同人员的身高、年龄和性别的列表,并想预测他们的体重。或者,我们可能有一些房屋数据,并想预测某所住宅的价值。
手头的问题在很大程度上决定着我们如何评估模型。
在分类中,我们想了解模型隔多久正确或不正确地识别新样本一次。而在回归中,我们可能更关注模型的预测值与真正值之间差多少。
我们会探讨几个性能指标。
-
对于分类,我们会探讨准确率、精确率、召回率和 F 分数。
-
对于回归,我们会探讨平均绝对误差和均方误差。
三、分类的指标
对于分类,我们处理的是根据离散数据进行预测的模型。这就是说,此类模型确定新实例是否属于给定的一组类别。在这里,我们测量预测是否准确地将所讨论的实例进行分类。
3.1 准确率Accuracy
准确率实际上是所有被正确标示的数据点除以所有的数据点。
- Shortcomings of accuracy
—— not ideal for skewed classes (不对称偏态分布)
—— 是否容忍误测?不能区别对待
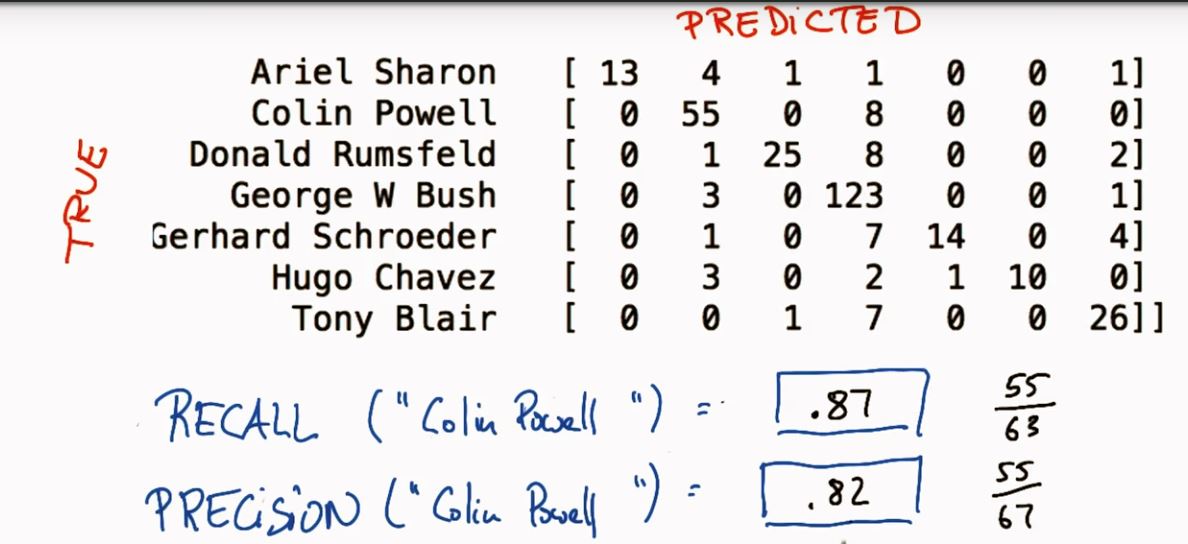
3.2 精确率和召回率
Recall(查全率)
Precision(查准率,精确率)
Accuracy(准确率)
摘录博客
相关概念请参考博客
五、混淆矩阵(confusion matrix)
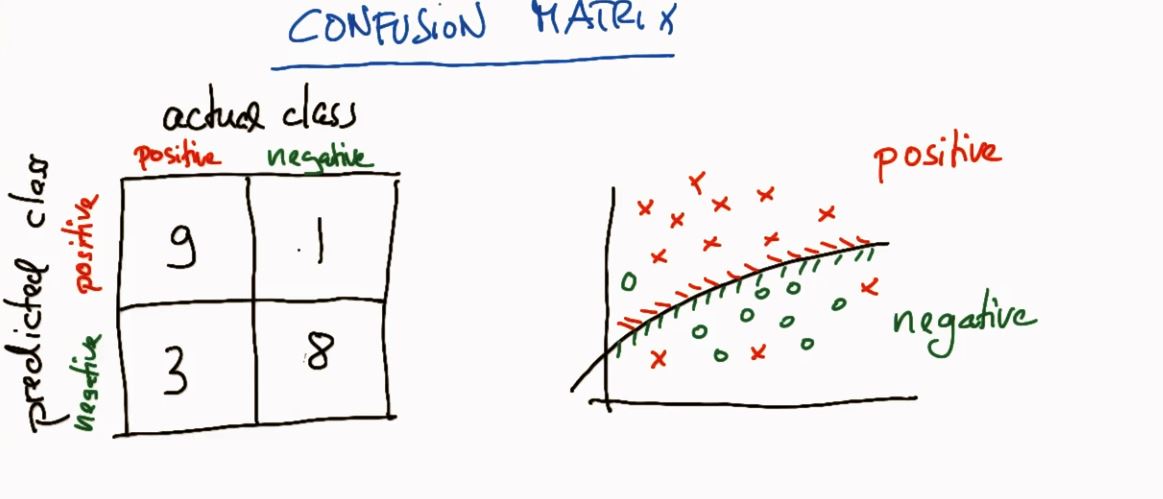
水平轴向为 actual class
- 混淆矩阵解释
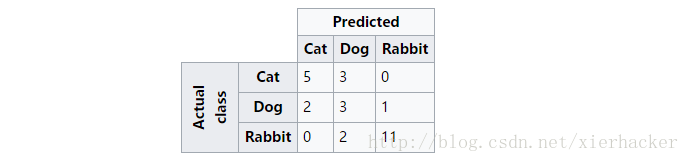
上面这幅图可以这么看,比如第一行,可以看做是猫中有5只预测为猫(即预测正确),有3只预测为狗,0只预测为兔子. 同样第二行可以理解为狗中有2只预测为猫,有3只预测为狗,1只预测为兔子…..依次类推.
可以看出来,对角线上面的是每一类别被正确预测的数量(概率),意味着,一个好的分类器得到的结果的混淆矩阵应该是尽可能的在对角线上面”成堆的数字”,而在非对角线区域越接近0越好,意味着预测正确的要多,预测错误的要少.
- True Positive(真正, TP):将正类预测为正类数.
- True Negative(真负 , TN):将负类预测为负类数.
- False Positive(假正, FP):将负类预测为正类数 →→ 误报 (Type I error).
- False Negative(假负 , FN):将正类预测为负类数 →→ 漏报 (Type II error).

__精确率(precision)__定义为:
需要注意的是精确率(precision)和准确率(accuracy)是不一样的,
在正负样本不平衡的情况下,准确率这个评价指标有很大的缺陷。比如在互联网广告里面,点击的数量是很少的,一般只有千分之几,如果用acc,即使全部预测成负类(不点击)acc 也有 99% 以上,没有意义。
__召回率(recall,sensitivity,true positive rate)__定义为:
通俗版本
刚开始接触这两个概念的时候总搞混,时间一长就记不清了。
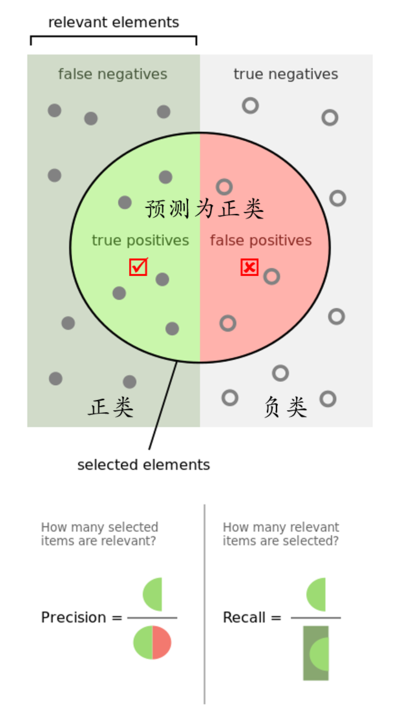
实际上非常简单,__精确率__是针对我们__预测结果__而言的,它表示的是预测为正的样本中有多少是对的。那么预测为正就有两种可能了,一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP)。
而__召回率__是针对我们原来的__样本__而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN)。
3.3 F1 分数
F1 分数会同时考虑精确率和召回率,以便计算新的分数。
可将 F1 分数理解为精确率和召回率的加权平均值,其中 F1 分数的最佳值为 1、最差值为 0:
F1 = 2 * (精确率 * 召回率) / (精确率 + 召回率)
F1是精确率和召回率的调和均值
精确率和准确率都高的情况下,F1 值也会高。
四、回归指标
正如前面对问题的回归类型所做的介绍,我们处理的是根据连续数据进行预测的模型。在这里,我们更关注预测的接近程度。
例如,对于身高和体重预测,我们不是很关心模型能否将某人的体重 100%
准确地预测到小于零点几磅,但可能很关心模型如何能始终进行接近的预测(可能与个人的真实体重相差 3-4 磅)。
4.1 平均绝对误差
在统计学中可以使用绝对误差来测量误差,以找出预测值与真实值之间的差距。平均绝对误差的计算方法是,将各个样本的绝对误差汇总,然后根据数据点数量求出平均误差。通过将模型的所有绝对值加起来,可以避免因预测值比真实值过高或过低而抵销误差,并能获得用于评估模型的整体误差指标。
有关平均绝对误差和如何在 sklearn 中使用它的更多信息,请查看此链接此处。
4.2 均方误差
均方误差是另一个经常用于测量模型性能的指标。与绝对误差相比,残差(预测值与真实值的差值)被求平方。
对残差求平方的一些好处是,自动将所有误差转换为正数、注重较大的误差而不是较小的误差以及在微积分中是可微的(可让我们找到最小值和最大值)。
4.3 回归分数指标
除了误差指标之外,scikit-learn还包括了两个分数指标,范围通常从0到1,值0为坏,而值1为最好的表现,看起来和分类指标类似,都是数字越接近1.0分数就越好。
- 1.R2分数,用来计算真值预测的可决系数。在 scikit-learn 里,这也是回归学习器默认的分数方法。
R2的数值范围从0至1,表示目标变量的预测值和实际值之间的相关程度平方的百分比。一个模型的R2 值为0还不如直接用平均值来预测效果好;而一个R2 值为1的模型则可以对目标变量进行完美的预测。从0至1之间的数值,则表示该模型中目标变量中有百分之多少能够用特征来解释。模型也可能出现负值的R2,这种情况下模型所做预测有时会比直接计算目标变量的平均值差很多。
from sklearn.metrics import r2_score
score = r2_score(y_true,y_predict)
- 2.可释方差分数
虽然眼下我们不会详细探讨这些指标,一个要记住的重点是,回归的默认指标是“分数越高越好”;即,越高的分数表明越好的表现。而当我们用到前面讲的误差指标时,我们要改变这个设定.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号