监督学习——朴素贝叶斯分类理论与实践
对于给定的训练数据,首先基于特征条件独立假设学习输入/输出的联合概率分布,然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率最大的输出y。
条件概率:
条件概率应该比较熟悉,P(A|B) 表示事件B已经发生的条件下,事件A发生的概率。计算公式如下:

贝叶斯定理:
独立性
事件的独立性:
假设 A,B是两个事件,如果满足等式: P(AB) = P(A)*P(B) ,则称时间A,B相互独立.
由条件概率公式知:如果两个事件独立则: P(A|B) = P(A) . (B的发生与否对于A的结果没有影响)
参数(随机变量)的独立性:
假设(x1,x2)是二位的随机变量,其联合分布函数为F(x1,x2),随机变量x1,x2的边缘分布函数为Fx1(x1)和Fx2(x2),如果对于任意x1,x2均有:
F(x1,x2) = Fx1(x1) * Fx2(x2)
该公式等价于: P{X1<x1,X2<x2} = P{X1<x1} * P{X2<x2}
则 x1, x2为相互独立的随机变量
在建模时,往往涉及到选取不同的特征变量(如颜色形状等等),这些参数的独立就是这里的参数独立。
先验概率
先验概率(prior probability)是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现的概率。
后验概率:
事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率。
假设一个学校里有60%男生和40%女生。女生穿裤子的人数和穿裙子的人数相等,所有男生穿裤子。一个人在远处随机看到了一个穿裤子的学生。那么这个学生是女生的概率是多少?
使用贝叶斯定理,事件A是看到女生,事件B是看到一个穿裤子的学生。我们所要计算的是P(A|B)。 P(A)是忽略其它因素,看到女生的概率,在这里是40% P(A')是忽略其它因素,看到不是女生(即看到男生)的概率,在这里是60% P(B|A)是女生穿裤子的概率,在这里是50% P(B|A')是男生穿裤子的概率,在这里是100% P(B)是忽略其它因素,学生穿裤子的概率,P(B) = P(B|A)P(A) + P(B|A')P(A'),在这里是0.5×0.4 + 1×0.6 = 0.8。
根据贝叶斯定理,我们计算出后验概率P(A|B) P(A|B)=P(B|A)*P(A)/P(B)=0.25 可见,后验概率实际上就是条件概率。
极大似然估计
用处:极大似然估计往往用来计算一个模型中的参数。 使用前提:“模型已定,参数未知”
原理:通过微分(如果有多个参数,可能需要解微分方程组)的方法寻找使样本集合(x1,x2,x3,x4…..)出现概率最大的模型参数。下面是概率论中通过极大似然估计,计算高斯分布的两个参数:(实际中的模型往往比高斯模型复杂的多,但是原理是一样的)
至于为什么一阶导数得到的方程组就能求得极大值,请参考这篇文章:http://www.cnblogs.com/hapjin/p/6633471.html
最大似然估计的一般求解过程:
(1) 写出似然函数;
(2) 对似然函数取对数,并整理;
(3) 求导数 ;
(4) 解似然方程
朴素贝叶斯法
假如一个样本的输入为X(可以为一个向量x1,x2,x3…),输出为Y(可以是分类问题,也可以是连续值)
假设: 条件独立性假设:用于分类的特征在类确定额条件下都是条件独立的。
朴素贝叶斯法通过训练数据集学习联合概率分布P(X,Y)。
先验概率: P(Y)
条件概率: P(X = x|Y = y)
条件独立性假设:
最终得到后验概率的计算公式(4.4) 及 贝叶斯分类器的计算公式(4.7)
注: 分母做了归一下处理(比较双方分母都化作1)
这里加一个问题: 为什么要条件独立性假设,而不是直接利用数据求解条件概率 P(X = x|Y = y)?
这里X涉及到关于x所有属性的联合概率,直接根据样本出现的概率来估计将会遇到严重的困难。例如,假设样本d个属性都是二值的将有2^d种可能的取值,在现实中这个往往大于训练样本数。
基于朴素贝叶斯的文本分类
需求
1. 邮件分为两类,一种为正常邮件,另一种为侮辱性邮件(标签分别用 0/1表示 )
2. 提供 正常邮件和侮辱性邮件(数据及其标签)
3. 当输入邮件数据时,系统需要输出其标签
文本数据预处理
1. 加载邮件数据以及他们的标签(邮件分类:是否为恶意邮件)
def loadDataSet():
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0,1,0,1,0,1] #1 is abusive, 0 not
return postingList,classVec
2. 基于已有的邮件构建”单词表“(所有邮件中包含的单词)
def createVocabList(dataSet):
vocabSet = set([]) #create empty set
for document in dataSet:
vocabSet = vocabSet | set(document) #union of the two sets
return list(vocabSet)
3. 将已有的邮件映射到词表中(如果邮件中某个单词出现则此表中该 位置为 1 否则为0)
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else: print "the word: %s is not in my Vocabulary!" % word
return returnVec
训练函数
将预处理好的数据输入到该函数中,就能得到上面公式4.7中: P(x=xi | Y=1)或者 P(x=xi | Y=0) 的每项概率保存在返回的两个数组。并且将 整体 的概率 P(Y=1) 也返回了。
# trainMatrix: 文本映射到“词表”中的矩阵 # trainCategory: 文本的 类别 def trainNB0(trainMatrix,trainCategory): numTrainDocs = len(trainMatrix) # 文本的数量 numWords = len(trainMatrix[0]) # 词表的长度 pAbusive = sum(trainCategory)/float(numTrainDocs) # 类别为1的概率 p0Num = ones(numWords); # 存放计算的条件概率 P(xi|Y=0) p1Num = ones(numWords) # 存放计算的条件概率 P(xi|Y=1) p0Denom = 2.0; p1Denom = 2.0 for i in range(numTrainDocs): if trainCategory[i] == 1: p1Num += trainMatrix[i] p1Denom += sum(trainMatrix[i]) else: p0Num += trainMatrix[i] p0Denom += sum(trainMatrix[i]) p1Vect = log(p1Num/p1Denom) #change to log() p0Vect = log(p0Num/p0Denom) #change to log() return p0Vect,p1Vect,pAbusive
邮件分类
根据贝叶斯公式分别计算一封邮件是正常邮件还是侮辱性邮件的概率,如下所示:
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1): p1 = sum(vec2Classify * p1Vec) + log(pClass1) #element-wise mult p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1) if p1 > p0: return 1 else: return 0
navie_bayes源码结构
BaseNB 接口
计算每种分类的似然概率
@abstractmethod
def _joint_log_likelihood(self, X):
I.e. ``log P(c) + log P(x|c)`` for all rows x of X, as an array-like of
shape [n_classes, n_samples].
分类
def predict(self, X): """ Perform classification on an array of test vectors X. Parameters ---------- X : array-like, shape = [n_samples, n_features] Returns ------- C : array, shape = [n_samples] Predicted target values for X """ jll = self._joint_log_likelihood(X) return self.classes_[np.argmax(jll, axis=1)]
针对源码中定义了三个对外类
GaussianNB (当特征变量为高斯分布时,原理查看scikit网站中介绍)
父类中函数实现
#计算均值和方差的函数
@staticmethod
def _update_mean_variance(n_past, mu, var, X, sample_weight=None):
# 父类中_joint_log_likelihood函数实现
def _joint_log_likelihood(self, X): check_is_fitted(self, "classes_") X = check_array(X) joint_log_likelihood = [] for i in range(np.size(self.classes_)):
# P(y)
jointi = np.log(self.class_prior_[i])
# siga_为方差 theta_为均值
n_ij = - 0.5 * np.sum(np.log(2. * np.pi * self.sigma_[i, :]))
n_ij -= 0.5 * np.sum(((X - self.theta_[i, :]) ** 2) /
(self.sigma_[i, :]), 1)
joint_log_likelihood.append(jointi + n_ij)
joint_log_likelihood = np.array(joint_log_likelihood).T
return joint_log_likelihood
参考:
《机器学习实战》
《统计学方法》
Scikit Learn: http://scikit-learn.org/stable/modules/naive_bayes.html#multinomial-naive-bayes


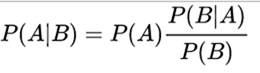

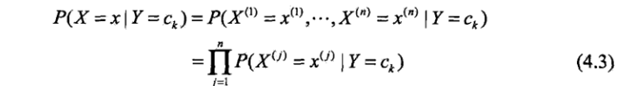



 浙公网安备 33010602011771号
浙公网安备 33010602011771号