监督学习——决策树理论与实践(上):分类决策树
1. 介绍
决策树是一种依托决策而建立起来的一种树。在机器学习中,决策树是一种预测模型,代表的是一种对象属性与对象值之间的一种映射关系,每一个节点代表某个对象/分类,树中的每一个分叉路径代表某个可能的属性值,而每一个叶子节点则对应从根节点到该叶子节点所经历的路径所表示的对象的值
通过训练数据构建决策树,可以高效的对未知的数据进行分类。决策数有两大优点:
1)决策树模型可以读性好,具有描述性,有助于人工分析;
2)效率高,决策树只需要一次构建,反复使用,每一次预测的最大计算次数不超过决策树的深度。
决策树是一颗树形的数据结构,可以是多叉树也可以是二叉树,决策树实际上是一种基于贪心策略构造的,每次选择的都是最优的属性进行分裂。
决策树也是一种监督学习算法,它的样本是(x,y)形式的输入输出样例。
输入:一组对象属性
输出:对象值(分类算法中得到某个类别)
决策树中间计算过程:
统计学习方法中根据下表贷款数据表生成的决策树如下,当给定一个人的特征属性之后就能判断能不能给他贷款。
由上面的示例可以看出决策树模型是一个 if(){}else if(){} else(){}模型,这里它具有一个十分重要的性质:互斥并且完备(每一个实例都被一条路径或者一条规则所覆盖,而且只被一条路径或一条规则所覆盖)
一般可以将决策树分为两种类型,一种是 分类决策树,也就是本篇所介绍的决策树类型。另一种决策树是 回归决策树(CART回归树),下一篇中再介绍。它们的主要区别是得到的结果是否是连续值还是一个类别(分类问题、回归问题)。

2. 分类决策树
看到上面的第一张决策树的图后,心中会产生几个疑问:
1) 为什么将“有自己的房子”作为根节点?
2) 为什么有自己的房子分类结果就是“是”?
3) 如何选定下一个节点?…..
先介绍一下决策树中必须明白的几个概念:
2.1 熵与条件熵、经验熵与检验条件熵
熵H(X):表示随机变量不确定性的度量,如果一个变量的随机性越大(不确定性),则它的熵越大。
计算公式:
条件熵H(Y|X):表示在已知随机变量X的条件下随机变量Y的不确定性。例如“有自己房子”条件下“贷款”的熵。
当熵和条件熵中的概率是由数据估计(特别是极大似然估计)得到时,所对应的熵与条件熵分别称为经验熵和经验条件熵。
2.2 信息增益与信息增益比
信息增益:表示得知特征的信息使得类Y的信息的不确定性减少程度。
特征A对训练数据集D的信息增益g(D,A):集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差。

假设数据D可以分为K个类(对应介绍中 贷款“是”,“否”),特征A(“有自己的房子”)有n个不同的取值(“有”,“无”)。
H(D): 对数据集D进行分类的不确定性。
H(D|A): 在特定A给定条件下对数据集D进行分类的不确定性。
它们的计算公式如下(统计学习方法中的解析)
既然已经有了信息增益为什么还要引入“信息增益比”呢?
在以信息增益划分到底采用那个特征时,存在偏向于选取值较多的特征的问题,所以这里引入的增益比相当于归一化,使各个特曾的影响因子归一化。
 其中:
其中:

3. 决策树算法——ID3 算法
当理解了上面信息熵和条件熵的概念后,ID3算法就很容易理解了。该算法解决的主要问题是:如何生成一个决策树?
输入:训练数据集D,特征集A,阈值e
输出: 决策树 T
3.1 决策树生成算法
ID3算法的核心是在决策树各个子节点上应用信息增益准则选择特征,递归的构建决策树,具体方法是:从根节点开始,对节点计算所有可能的特征的信息增益,选择信息增益最大的特征作为节点的特征,由该特征的不同取值建立子节点;再对子节点递归调用以上方法,构建决策树。直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。
这其中会遇到一些问题:
1、若D中所有的实例属于用一类C(k),则T为单节点数,并将类C(k)作为该节点的类标记
2、若A = null,则T为单节点树,并将D中实例数最大的类C(k)作为该节点的类标记。
3、如果A(g)的信息增益比小于阈值e,则置T为单节点树,并将D中实例数最大的类作为该节点的类标记。
4、随着树的向下生长,特征集也会逐渐减少(A-A(g)),父节点中出现的特征将会排除在特征选取中。
与ID3算法类似的算法 C4.5算法,与ID3唯一的不同是 它选取信息增益比作为特征选择的标准,这样可以减少过拟合。而ID3采用信息增益作为特征选择的标准。
创建决策树的伪代码(createBranch函数):
1 检测数据中的每个子项是否属于同一个分类 2 if so return 类标签 3 else 4 寻找划分数据集的最好特征 5 划分数据集 6 创建分支节点 7 for 每个划分的子集 8 调用 createBranch并增加返回结果到分支节点中 9 return 分支节点
3.2 决策树的减枝
通过决策树算法生成的决策树往往对训练数据的分类很精确,但对未知的测试数据的分类却没有那么准确,即出现过拟合现象。
在决策树学习中将已生成的树进行简化的过程称为剪枝。
决策树的剪枝往往通过极小化决策树整体的损失函数/代价函数来实现。 当剪枝后决策树的损失值小于剪枝前损失函数值,那么该分支将会被剪掉。(从叶节点自下而上遍历决策树的每个节点,确定是否需要进行剪枝)
3.3 决策树的损失函数:
《统计学习方法》中给出了损失函数的公式:
4. python 实现ID3决策树生成
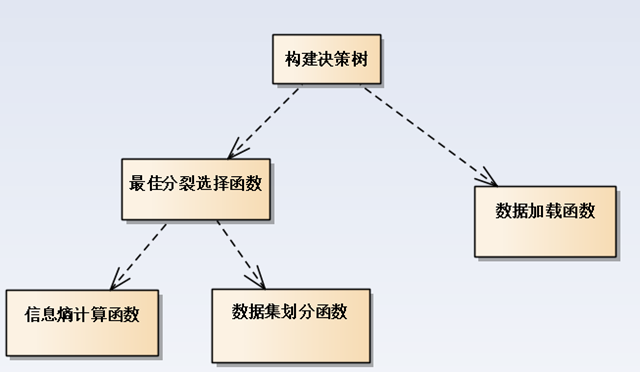
决策树构建的组件图如下:
数据准备(只作为算法测试)
def createDataSet(): dataSet = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] labels = ['no surfacing','flippers'] #change to discrete values return dataSet, labels
1. 计算信息熵的函数:
注: 输入数据的最后一列为 数据标签。
def calcShannonEnt(dataSet): numEntries = len(dataSet) labelCounts = {} for featVec in dataSet: #the the number of unique elements and their occurance currentLabel = featVec[-1] if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 shannonEnt = 0.0 for key in labelCounts: prob = float(labelCounts[key])/numEntries shannonEnt -= prob * log(prob,2) #log base 2 return shannonEnt
2. 划分数据集
该函数的目的是筛选出 某一列值等于某个只的所有数据,放到一个新的矩阵中:
# dataSet: 原始测试数据 # axis : 测试数据的某一列 # value: 需要筛选的值 def splitDataSet(dataSet, axis, value): retDataSet = [] for featVec in dataSet: if featVec[axis] == value: reducedFeatVec = featVec[:axis] #chop out axis used for splitting reducedFeatVec.extend(featVec[axis+1:]) retDataSet.append(reducedFeatVec) return retDataSet
3. 计算最佳的数据划分方式
计算信息增益选取最佳的数据划分方式. (分别计算每个特征值的信息增益值,返回信息增益最大的特征值序号)
def chooseBestFeatureToSplit(dataSet): numFeatures = len(dataSet[0]) - 1 #特征值的数量 baseEntropy = calcShannonEnt(dataSet) bestInfoGain = 0.0; bestFeature = -1 #最佳特征值 for i in range(numFeatures): #遍历每个特征值,计算信息增益 featList = [example[i] for example in dataSet] # 存放第i列,数据值的set uniqueVals = set(featList) #get a set of unique values newEntropy = 0.0 for value in uniqueVals: subDataSet = splitDataSet(dataSet, i, value) prob = len(subDataSet)/float(len(dataSet)) newEntropy += prob * calcShannonEnt(subDataSet) infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy if (infoGain > bestInfoGain): #compare this to the best gain so far bestInfoGain = infoGain #if better than current best, set to best bestFeature = i return bestFeature #returns an integer
注: 这里运用了信息增益,而并没有使用信息增益比。
4.递归构建决策树
有了前面的函数工具基础,构建一颗决策树也就不那么复杂了。
def createTree(dataSet,labels): classList = [example[-1] for example in dataSet] if classList.count(classList[0]) == len(classList): return classList[0]#stop splitting when all of the classes are equal #stop splitting when there are no more features in dataSet if len(dataSet[0]) == 1: return majorityCnt(classList) bestFeat = chooseBestFeatureToSplit(dataSet) bestFeatLabel = labels[bestFeat] myTree = {bestFeatLabel:{}} del(labels[bestFeat]) featValues = [example[bestFeat] for example in dataSet] uniqueVals = set(featValues) for value in uniqueVals: subLabels = labels[:] #copy all of labels, so trees don't mess up existing labels #递归调用,createTree函数 myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels) return myTree
参考:
《统计学习方法》
《机器学习实战》
http://blog.csdn.net/jialeheyeshu/article/details/51832165


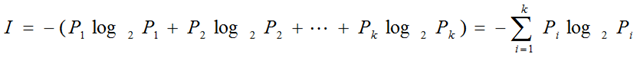
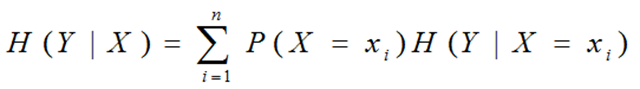





 浙公网安备 33010602011771号
浙公网安备 33010602011771号