20180909徐州网络赛题解
20180909徐州网络赛题解
A. Hard to prepare
MEANING
n个点的环,每个点在[0,\(2^{k-1}\)] 之间选一个值。要求相邻两点的权值的二进制至少有一位相同。问方案数
SOLUTION
断环为链,类似染色问题递归推导,考虑到爆栈,可能要把递归改成递推
CODE
队友代码
#include <bits/stdc++.h>
using namespace std;
const long long mod=1e9+7;
long long qpow(long long a,long long b)
{
long long res=1;
while(b)
{
if(b%2)
res = res*a%mod;
a = a*a%mod;
b = b/2;
}
return res;
}
long long n,k;
long long dp[1000005];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%lld %lld",&n,&k);
long long x;
x = qpow(2,k);
dp[1] = x;
dp[2] = x*(x-1)%mod;
for(int i=3;i<=n;i++)
{
dp[i] = ( dp[i-2]*(x-1)%mod + ( x*qpow((x-1+mod)%mod,i-2)%mod-dp[i-2] +mod )%mod*(x-2)%mod )%mod;
}
printf("%lld\n",dp[n]);
}
return 0;
}
B. BE, GE or NE
MEANING
两个人玩一个galgame,一个人想GoodEnding,另一个想BadEnding。两人轮流选择剧情分支,剧情分支有三种,一种会使好感度增加,第二种会使好感度减少,第三种会使好感度取反。两人都很聪明,问游戏最后结局(只取决于好感度)如何。
SOLUTION
由于范围很小,考虑dp
CODE
队友代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const ll maxn = 1000005;
const ll mod = 1000000007;
ll n,m,k,l;
ll dp[1005][205];
ll a[1005][5];
int main() {
scanf("%lld%lld%lld%lld",&n,&m,&k,&l);
k+=100;
l+=100;
m+=100;
for (int i=1; i<=n; i++) {
for (int j=1; j<=3; j++) {
scanf("%lld",&a[i][j]);
}
}
for (int j=0; j<=200; j++)
dp[n+1][j]=j;
for (int i=n; i>=1; i--) {
for (int j=200; j>=0; j--) {
if (i%2) {
dp[i][j]= 0;
if (a[i][1])
dp[i][j]= max(dp[i][j],dp[i+1][min(j+a[i][1],200ll)]);
if (a[i][2])
dp[i][j]= max(dp[i][j],dp[i+1][max(j-a[i][2],0ll)]);
if (a[i][3])
dp[i][j]= max(dp[i][j],dp[i+1][200-j]);
} else {
dp[i][j]= 200;
if (a[i][1])
dp[i][j]= min(dp[i][j],dp[i+1][min(j+a[i][1],200ll)]);
if (a[i][2])
dp[i][j]= min(dp[i][j],dp[i+1][max(j-a[i][2],0ll)]);
if (a[i][3])
dp[i][j]= min(dp[i][j],dp[i+1][200-j]);
}
}
}
ll ans = dp[1][m];
if (ans>=k)
printf("Good Ending\n");
else if (ans<=l)
printf("Bad Ending\n");
else
printf("Normal Ending\n");
return 0;
}
F. Features Track
CODE
队友代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const ll maxn = 1000005;
const ll mod = 1000000007;
map<pll,ll> mp[2];
int main() {
ll t;
scanf("%lld",&t);
while(t--) {
ll n;
scanf("%lld",&n);
ll cur = 0;
mp[0].clear();
mp[1].clear();
ll ans = 0;
for (ll i=1; i<=n; i++) {
ll pre = cur;
cur = 1-cur;
mp[cur].clear();
ll k ;
scanf("%lld",&k);
set<pll> ss;
for (ll j=1; j<=k; j++) {
ll x,y;
scanf("%lld%lld",&x,&y);
pll cat = pll(x,y);
ll val = 1 + mp[pre][cat];
ans = max(ans,val);
mp[cur][cat]=val;
}
}
printf("%lld\n",ans);
}
return 0;
}
G. Trace
MENING
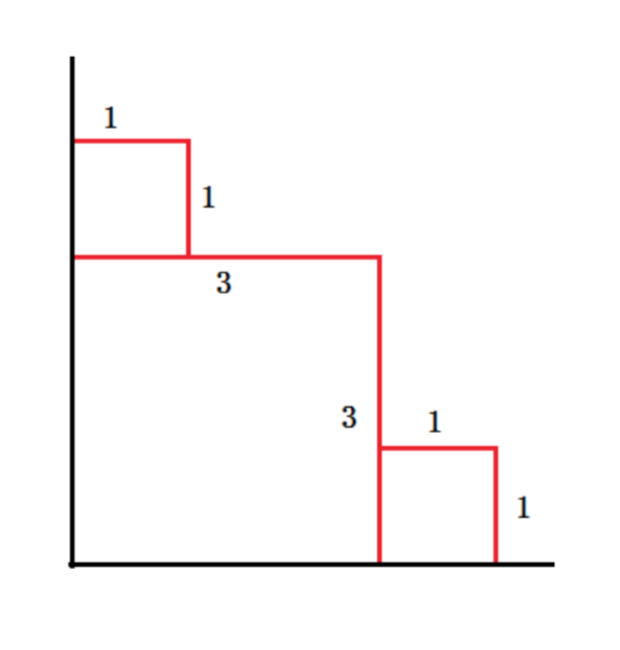
在平面坐标系xOy的第一象限中,给你一个点,分别向xy轴作垂线可以和坐标轴围成一个矩形。现在依次给出n个点,后来的矩形会覆盖前面的,保证一个矩形不会被完全覆盖,问图中红线长度。
SOLUTION
我们可以倒序向图中加入点。
每当一个点加入时,分别向xy轴作垂线直到碰到红线时停下,答案就会增加所画线段的长度。
可以分别对x轴y轴建线段树,区间修改,单点查询。注意需要离散化。
CODE
#define FILE_IN() freopen("C:\\Users\\dmt\\Desktop\\in.txt","r",stdin);
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 50005;
struct sgt {
struct SegmentTree {
int l,r;
ll sum,add;
#define l(x) tree[x].l
#define r(x) tree[x].r
#define sum(x) tree[x].sum
#define add(x) tree[x].add
} tree[MAXN<<2];
int a[MAXN],n;
void build(int p,int l,int r) {
l(p) = l,r(p) = r;
if(l==r) {
sum(p) = a[l];
return;
}
int mid = (l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
sum(p) = sum(p*2) + sum(p*2+1);
}
void spread(int p) {
if(add(p)) {
sum(p*2)+=add(p)*(r(p*2)-l(p*2)+1);
sum(p*2+1)+=add(p)*(r(p*2+1)-l(p*2+1)+1);
add(p*2)+=add(p);
add(p*2+1) += add(p);
add(p) = 0;
}
}
void change(int p,int l,int r,int d) {
if(l<=l(p)&&r>=r(p)) {
sum(p)+=(ll)d*(r(p)-l(p)+1);
add(p)+=d;
return;
}
spread(p);
int mid = (l(p)+r(p))/2;
if(l<=mid)change(p*2,l,r,d);
if(r>mid) change(p*2+1,l,r,d);
sum(p) = sum(p*2)+sum(p*2+1);
}
ll ask(int p,int l,int r) {
if(l<=l(p)&&r>=r(p))return sum(p);
spread(p);
int mid = (l(p)+r(p))/2;
ll val = 0;
if(l<=mid)val+=ask(p*2,l,r);
if(r>mid)val+=ask(p*2+1,l,r);
return val;
}
} axis_x,axis_y;
struct data{
int x,y,ind;
int lx,ly;
}point[MAXN];
int lisan_x[MAXN],lisan_y[MAXN];
bool cmpx(data a,data b){
if(a.x!=b.x)return a.x<b.x;
return a.ind<b.ind;
}
bool cmpy(data a,data b){
if(a.y!=b.y)return a.y<b.y;
return a.ind<b.ind;
}
bool cmp(data a,data b){
return a.ind<b.ind;
}
int main() {
// FILE_IN();
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d",&point[i].x,&point[i].y);
point[i].ind = i;
}
//离散化
sort(point+1,point+n+1,cmpx);
for(int i=1;i<=n;i++){
lisan_x[i] = point[i].ind;
point[i].lx = i;
}
sort(point+1,point+n+1,cmpy);
for(int i=1;i<=n;i++){
lisan_y[i] = point[i].ind;
point[i].ly = i;
}
sort(point+1,point+n+1,cmp);
for(int i=1;i<=n;i++){
axis_x.a[i] = axis_y.a[i] = 0;
}
//建线段树
axis_x.build(1,1,n);
axis_y.build(1,1,n);
ll ans = 0;
for(int i = n;i>=1;i--){
ll lx = point[i].lx;
ll ly = point[i].ly;
ll x = point[i].x;
ll y = point[i].y;
ll downy = axis_x.ask(1,lx,lx);
ll downx = axis_y.ask(1,ly,ly);
ans += x-point[lisan_x[downx]].x;
ans += y-point[lisan_y[downy]].y;
axis_x.change(1,downx,lx,ly-downy);
axis_y.change(1,downy,ly,lx-downx);
}
cout<<ans<<endl;
return 0;
}
H. Ryuji doesn't want to study
MEANING
给一个长度为n的数组a[n],q次询问,每次询问给出一个长度为L的区间[l,r],回答
a[l]×L+a[l+1]×(L−1)+⋯+a[r−1]×2+a[r]
CODE
队友代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const ll maxn = 1000005;
const ll mod = 1000000007;
ll n,q;
struct ST {
ll c[maxn];
ll lowbit(ll x) {
return -x&x;
}
void update(ll x,ll v) {
while(x<=n) {
c[x]+=v;
x+=lowbit(x);
}
}
ll query(ll x) {
ll ret = 0;
while(x>0) {
ret+=c[x];
x-=lowbit(x);
}
return ret;
}
ll query(ll l,ll r) {
return query(r)-query(l-1);
}
} s1,s2;
ll a[maxn];
int main() {
scanf("%lld%lld",&n,&q);
for (int i=1; i<=n; i++) {
scanf("%lld",&a[i]);
s1.update(i,a[i]*(n-i+1));
s2.update(i,a[i]);
}
for (ll qq =1; qq<=q; qq++) {
ll op;
scanf("%lld",&op);
if (op==1) {
ll l,r;
scanf("%lld%lld",&l,&r);
ll ans = s1.query(l,r) - s2.query(l,r)*(n-r);
printf("%lld\n",ans);
} else {
ll x,y;
scanf("%lld%lld",&x,&y);
s2.update(x,y-a[x]);
s1.update(x,(y-a[x])*(n-x+1));
a[x]=y;
}
}
return 0;
}
I. Characters with Hash
签到题
CODE
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const ll maxn = 1000005;
const ll mod = 1000000007;
char str[maxn];
int cnt = 0;
int main() {
ios::sync_with_stdio(false);
cin.tie();
int t;
cin>>t;
while(t--) {
int n;
char ch;
cin>>n;
cin>>ch;
cin>>str;
cnt = 0;
for (int i=0; i<n; i++) {
int tmp = abs(ch-str[i]);
if (tmp==0)
cnt+=2;
else if (tmp<10) {
cnt++;
break;
} else
break;
}
int ans = n*2-cnt;
if (ans==0)
ans=1;
cout<<ans<<endl;
}
return 0;
}
J. Maze Designer
MEANING
给一个n*m的网格图,给出每个格子与它相邻格子之间建堵墙的花费,要你找到一种建墙方案,使得在满足图中任意两个格子只有一条路径的前提下,总花费最小。然后就该方案给出q次询问,每次询问给定的两点之间的距离。
SOLUTION
题目要求图中任意两个格子只有一条路径,实际上就是一棵树。既然建墙(拆边)的总花费要最小,那么建边的总花费就是最大。所以跑一边Kruskal,求出最大生成树,时间复杂度O(nmlog(nm))。在树上询问两点之间的距离可以通过求出最近公共祖先,两点之间的距离就是dist(x,y) = deep(x)+deep(y)-2*deep(LCA(x,y)),时间复杂度O(qlog(nm))。
CODE
#define FILE_IN() freopen("C:\\Users\\dmt\\Desktop\\in.txt","r",stdin);
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 250005;
const int MAXE = 500005;
int n,m,t;
struct rec{
int x,y,z;
}mapp[500010];
int cnt;
bool cmp(rec a,rec b){
return a.z>b.z;
}
struct edge{
int u,v,w,nex;
}ed[MAXE];
int head[MAXN],tot;
void addedge(int u,int v,int w){
tot++;
ed[tot].u = u;
ed[tot].v = v;
ed[tot].w = w;
ed[tot].nex = head[u];
head[u] = tot;
}
int fa[MAXN];
int DjsGet(int x){
if(x==fa[x])return x;
return fa[x] = DjsGet(fa[x]);
}
int deep[MAXN],anc[MAXN][20];
queue<int> q;
void bfs() {
q.push(1);
deep[1] = 1;
while(q.size()) {
int x = q.front();
q.pop();
for(int i=head[x]; i; i=ed[i].nex) {
int y = ed[i].v;
if(deep[y])continue;
deep[y] = deep[x]+1;
anc[y][0] = x;
for(int j=1;j<t;j++){
anc[y][j] = anc[anc[y][j-1]][j-1];
}
q.push(y);
}
}
}
int lca(int x,int y) {
if(deep[x]<deep[y])swap(x,y);
for(int i=t-1; i>=0; i--) //to same deep;
if(deep[y]<=deep[anc[x][i]])
x = anc[x][i];
if(x==y)return x;
for(int i=t-1; i>=0; i--)
if(anc[x][i]!=anc[y][i]) {
x = anc[x][i];
y = anc[y][i];
}
return anc[x][0];
}
int main() {
// FILE_IN();
scanf("%d%d",&n,&m);
t = (int)log(n*m)/log(2)+1;
getchar();
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
int u = i*m+j+1;
char D,R;
D = getchar();
int w;
scanf("%d",&w);
getchar();
if(D=='D'){
int v = (i+1)*m+j+1;;
mapp[++cnt] = {u,v,w};
}
R = getchar();
scanf("%d",&w);
getchar();
if(R=='R'){
int v = i*m+j+2;
mapp[++cnt] = {u,v,w};
}
}
}
sort(mapp+1,mapp+cnt+1,cmp);
for(int i = 1;i<=n*m;i++)fa[i] = i;
for(int i=1;i<=cnt;i++){
int x = DjsGet(mapp[i].x);
int y = DjsGet(mapp[i].y);
if(x==y)continue;
fa[x] = y;
addedge(mapp[i].x,mapp[i].y,mapp[i].z);
addedge(mapp[i].y,mapp[i].x,mapp[i].z);
}
bfs();
int q;
scanf("%d",&q);
while(q--){
int x_1,y_1,x_2,y_2;
scanf("%d%d%d%d",&x_1,&y_1,&x_2,&y_2);
int u = (x_1-1)*m+y_1;
int v = (x_2-1)*m+y_2;
int la = lca(u,v);
printf("%d\n",deep[u]+deep[v]-2*deep[la]);
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号