熵以及熵函数

熵以及熵函数

0.前言

为了发现组合关系，在这里引进熵以及熵函数的概念。

1.问题引入

（1）引题1

在上次课我们知道，具有组合关系的词汇往往是共同出现，那么问题来了：当“eat”出现的时候，什么词也会同时出现呢（包括左边和右边）？

 

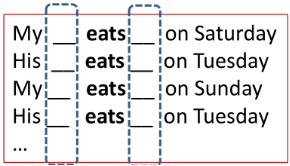
（2）引题2

上面的这个来自上节课的问题其实可以一般化，即预测词W是否出现在这篇文本里，如下图所示：

 

下面哪个词更有可能出现呢？

 

 

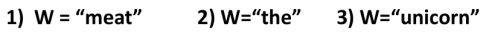
2.进入正题

要解决这个问题，首先我们将这个问题抽象成数学问题。我们先定义这样一个二值随机变量，如下所示：

 

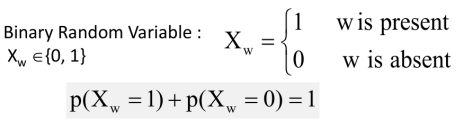
显然，词W出现的概率与词W未出现的概率加和为1。

可想而知，当这个随机变量的随机性越大，预测就越困难。那么，怎么来量化度量这个随机变量的随机性呢？

基于这个问题，我们引入信息论中熵以及熵函数的概念，以此来量化度量这种随机性。其公式如下所示：

 

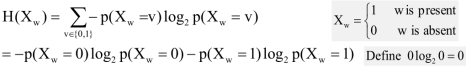
其中，规定，该函数式非负的，这在数学上是可证明的。

我们画出这个函数的函数图像进一步观察这个函数，其函数图像如下所示：

 

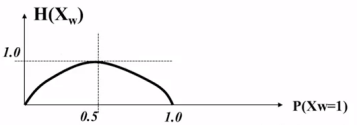
从这个图像我们可以看到，①这个函数图像是对称的；②它在中点处达到最大值，在两端达到最小值。为了更加深入地理解这个函数以及它的作用，举一个具体的例子，例子如下：

抛硬币，有两种硬币，一种是正常的硬币，一种是只会出现“人头”这面的硬币，在对这两种硬币抛出后对其结果进行预测，哪一种硬币的结果更容易预测？

解：第一种正常硬币的熵值：

 

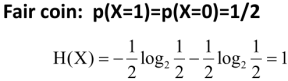
第二种硬币的熵值：

 

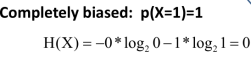
最后可以看出，第二种硬币抛出去后更容易预测，这是显然的，因为只会出现一种结果，那就是“人头”面。

3.最后

最后让我们回到我们开始时的词W的预测问题，下面三个词那个词更可能出现在一篇文本中？或说更容易预测呢？

 

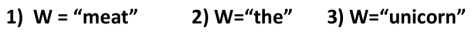
回答是，“the”的熵值最小，因为几乎在每一篇文本中the都会出现，它出现的概率太高，几乎为1，根据熵函数图像可以看出，其熵值几乎为0。

“unicorn”这个词在文本中出现的概率比较小，根据熵函数图像，它的熵值就比较小。

“meat”的熵值就比较大了，介于其余两者熵值之间。

4.结论

熵值越大，则其是否出现就越难被预测。