国庆题目
Maximize the Largest Component (Hard Version)
- 题意:
给定一个 \(n\times m\) 的网格,由“.”和“#”字符组成。
如果从该组中的任何单元格开始,通过仅移动到该组中共享一个共同边的另一个单元格,就可以到达该组中的任何其他单元格,则一组“#”单元格形成一个连通分量。其大小为该组中的单元格数量。
在一次操作中,选择任意一行 \(r\) 和任意一列 \(c\),然后将行 \(r\)和列 \(c\) 中的每个单元格设置为 "#"。
问在最多执行一次操作后,可以实现的“#”个单元格的最大连通分量的最大可能大小。
ps:保证所有测试用例中的 $ n \cdot m $ 的总和不超过 $ 10^6 $。
- 思路:
我们考虑到执行操作不会使答案更劣,所以我们一定会执行这次操作。
考虑到 \(n\times m\leq 10^6\),那么我们可以暴力枚举选择哪行哪列。
考虑到如果在枚举内部统计答案不好做,哥们考虑预处理答案,那么可以单点算贡献。
我们看下一个点会在选哪行哪列时产生贡献。
显然如果该点在原本的图上最左边可到达 \(l1\),最右可到达 \(r1\),最上可到达 \(l2\),最下 \(r2\) 的话,那么哥们会发现,只要我们选的行在 \([l2-1,r2+1]\) 的区间内或所选的列在 \([l1-1,r1+1]\) 的区间内,都可以产生贡献。
那么我们将我们的选择也抽象成一个矩阵,第 \(i\) 行 \(j\) 列记录的就是我们选第 \(i\) 行第 \(j\) 列的答案。
然后就变成一个套路的矩阵中一块的加减法,直接弄一个矩阵差分即可转为 \(O(1)\) 处理,最后再转回来即可,记得特殊处理你选的那行和那列的答案。
时间复杂度 \(O(nm)\)。
CF1984F
- 题意:
有一个长度为 \(n\) 的隐藏数组 \(a_1, a_2, \ldots, a_n\),其元素是介于 \(-m\) 和 \(m\) 之间的整数。
给你一个长度为 \(n\) 的数组 \(b_1, b_2, \ldots, b_n\) 和一个长度为 \(n\) 的字符串 \(s\),字符串由 \(\texttt{P}\) 、 \(\texttt{S}\) 和 \(\texttt{?}\) 组成。
对于从 \(1\) 到 \(n\) (含)的每个 \(i\),我们必须有:
- 如果是 \(s_i = \texttt{P}\), \(b_i\) 是 \(a_1\) 到 \(a_i\) 的和。
- 如果 \(s_i = \texttt{S}\), \(b_i\) 是 \(a_i\) 到 \(a_n\) 的和。
输出使得数组 \(a\) 符合要求的将 \(s\) 中的所有 \(\texttt{?}\) 替换为 \(\texttt{P}\) 或 \(\texttt{S}\) 的方案个数。
由于答案可能很大,因此输出答案对 \(998244353\) 取模的结果。
ps:\(2\leq n\leq 2\times 10^3\)
- 思路:
可以先从简单入手,我们先考虑没有 \(?\) 的情况,
那么我们手玩一下会发现,我们一定能得到数列的总和,因为只要第一个是 \(S\) 或者最后一个是 \(P\) 或者 \(s\) 中有一个 \(PS\) 就一定能得到总和。
然后哥们手玩一下这些限制的关系(\(sum\) 为数列和):
-
\(PP\) 限制了 \(b_i-b_{i-1}=a_i\),而 \(a_i\) 是有范围的(下同)。
-
\(SP\) 限制 \(sum+b_i+b_{i-1} = a_i+a_{i-1}\)
-
\(PS\) 限制 \(sum=a_i+a_{i-1}\)
-
\(SS\) 限制 \(b_{i-1}-b_i=a_i\)
那也就是说,如果我们真的知道这个 \(sum\),我们就可以用 dp 求出方案数。
观察到 \(n\) 的范围,我们可以直接枚举这个 \(sum\) 在那个位置出现(即上文提到的 \(sum\) 的出现方式),然后 dp 即可,时间复杂度 \(O(n^2)\)。
Shuffle
- 题意:
给定一棵 \(n\) 个结点的树,定义对一棵树的操作如下:
- 从树中任选一个节点,把这个结点作为新树的根结点;
- 从原树中删除选中结点,并对于剩下的每个连通块(如果有的话)做同样的操作;
- 令选中的结点与每个连通块操作后的新树的根连边,形成一棵新树。
求对于给定的树做一次如上操作生成新树的叶结点数量最大值。每个测试点 \(t\) 组测试用例。
-
\(1\le t\le 10^4\);
-
\(1\le n\le 2\cdot 10^5\);
-
\(\sum n\le 3\cdot 10^5\)。
-
思路:
考虑到其实题意就是将这棵树不断删点,然后最后剩下的度为 \(0\) 的点最多,其实就是求树的最大不连通点集,然后这个容易用 dp 求出,但是你会发现,写完后交上去过不了,因为这个翻译有锅(大概。
就是原题中定义的叶子结点是:
Note that leaves are all nodes with degree \(1\) . Thus, the root may be considered as a leaf if it has only one child.
也就是说,如果根只有一个子项,那么他也要算在答案中,但是翻译中并没有提到这点。
那么关于这点,其实就是约等于将原树删去一个度为 \(1\) 的点后再求最大不连通子集,最后加 \(1\)。
那么哥们可以将 dp 做一个微调,\(f_{p,0/1,0/1}\) 为该点 \(p\) 选与不选,去掉或还没去掉叶子结点的最大不连通点集,然后常规转移就行了。
"a" String Problem
- 题意:
给定一个字符串 \(s\),求有多少不同的非空字符串 \(t\),使得存在一种分割 \(s\) 至若干子串 \(p_1 \sim p_k\) 的方法满足:
- \(p_i \in \{t, \texttt a\}\)。
- 至少存在一个 \(i\) 满足 \(p_i = t\)。
ps:\(1\leq t\leq 10^4,2\leq |s| \leq 2\cdot 10^5,\sum |s|\leq 3\cdot 10^5\)
- 思路:
哥们注意到假设 \(t\) 中有 \(b\) 个非 \(a\) 字符,将 \(s\) 去掉所有 \(a\)(假设剩 \(c\) 个字符),那么显然 \(\dfrac{c}{b}\) 且 \(b|c\),不然显然不符合割的定义。
那么哥们枚举 \(c\) 的因数,得到 \(b\) 的大小,然后直接按规定割就行,然后我们还要考虑 \(t'\) 能向前延伸多少个 \(a\),向后能延伸多少个 \(a\),这个可以按割出的 \(t'\) 的间隙的大小得到限制,然后答案就是限制相乘。
但是我们考虑到,可能 \(b=0\),也就是说,\(t\) 是一个全 \(a\) 的东西,那么此时 \(s\) 一定是一个全 \(a\) 的字符串,直接特判掉就行了。
array-value
- 题意:
给定序列 \(a\)。定义长度大于 \(1\) 的区间 \([l, r]\) 的权值为 \(a_i \oplus a_j\) 的最小值,其中 \(l\leq i \lt j \leq r\),\(\oplus\) 表示异或。求所有长度大于 \(1\) 的子区间的第 \(k\) 小权值。
\(2\leq n\leq 10 ^ 5\),\(1\leq k\leq \frac {n \cdot (n - 1)} 2\),\(0\leq a_i\leq 10 ^ 9\)。
- 思路:
我们考虑二分这个答案,然后转为判定性问题。
假设哥们二分一个答案为 \(mid\),那么现在也就是问有几个区间,其权值是 \(\leq mid\)。
那么由于区间重复问题,哥们为了不算重,考虑枚举这个区间右端点 \(r\),那么我们现在需要找一个左端点,他是 \(r\) 左边第一个使得区间权值 \(\leq mid\) 的点(因为再往左一定包含)。
然后这些关于位运算的东西,哥们可以尝试给他转成树上问题,假设我们把他们的二进制数按顺序整到一棵 \(tire\) 树上,然后我们考虑什么时候,异或出来的东西是 \(\leq mid\) 的,考虑分讨:
我们假设当前数第 \(x\) 位为 \(a\),\(mid\) 第 \(x\) 位为 \(b\)。
-
\(a=0,b=0\) 那么异或上的数的第 \(x\) 位应该顺着 \(1\) 走。
-
\(a=0,b=1\) 那么异或上的数的第 \(x\) 位是 \(0\) 的都行,这里可以维护一个子树左端点最大值,然后 \(1\) 就顺着走。
-
\(a=1,b=0\) 那么异或上的数的第 \(x\) 位应顺着 \(1\) 走。
-
\(a=1,b=1\) 那么异或上的数的第 \(x\) 位是 \(1\) 的都行,这里可以维护一个子树左端点最大值,然后 \(0\) 就顺着走。
然后就以 \(O(n\log^2 V)\) 的时间通过了该题,\(V\) 为值域。
I Love Balls
- 题意:
Alice 和 Bob 在玩游戏。他们面前有 \(n\) 个球,第 \(i\) 个球的价值为 \(v_i\),且前 \(k\) 个球为“特殊球”,Alice 为先手。每一轮,Alice 或 Bob 会随机从剩余的球中选取一个球并把它取出,获得它的价值。如果这个球为特殊球,则下一轮的玩家不变,否则下一轮的玩家改变。问 Alice 和 Bob 各自得到的价值的期望对 \(10^9 + 7\) 取模的值。
ps:\(1\leq k\leq n\leq 4\cdot 10^5\),\(1\leq v_i\leq 10^7\)
- 思路:
首先显然每种方案的概率是一样的,这个概率具体而言即:
我们先考虑忽略球的序号的方案,我们发现这个和前面一场模拟赛的 T1 很类似,即:
\(\dfrac{A!\times B!}{n!}\)
然后对于每个不管序号的方案,他们加上序号的影响都是 \(K!\times (n-K)!\)(即你按顺序一一对应)
那么总的概率就是:
\(\dfrac{A!\times B!}{n!\times K!\times (n-K)!}\)
然后问题变为求权值和。
那么我们手玩一下,发现无论特殊点的状态如何,普通点的分配只和 \(n-K\) 的奇偶性有关。
那么枚举 \(Alice\) 拿了 \(x\) 个黑点(特殊点),所以 \(Bob\) 拿了 \(y=K-x\) 个黑点。
然后已知 \(Alice\) 拿了 \(a = \left\lceil\dfrac{n-K}{2}\right\rceil\) 个白点(普通点),\(Bob\) 拿了 \(b = n-K-a\) 个白。
然后你大眼观察,发现 \(Alice\) 的黑点可以随便插入 \(Alice\) 的白点的空隙中,但是特殊的,当 \(Alice\) 的白比 \(Bob\) 的白多一个时,\(Alice\) 的黑点是不能插到最后的白点的后面的,原因显然(\(Alice\) 比 \(Bob\) 多一个白,那么 \(Alice\) 拿万白后应为 \(Bob\) 拿)
然后 \(Bob\) 的黑点可以在容易地方插入。
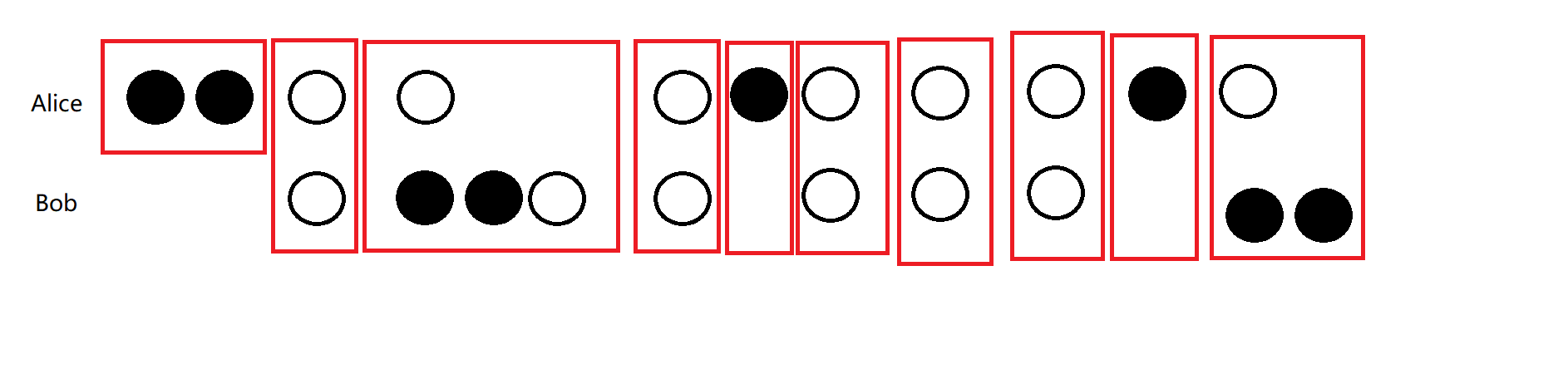
一个红框即为一对白,\(Bob\) 的黑可以插到任意一个红框中,\(Alice\) 的能插到红框的间隙中(最前面永远可以,最后面看奇偶,如上图就不行)、
然后求权值和,由于两人的求法并无本质上的区别,这里只讨论求 \(Alice\) 的。
首先容易发现黑点和白点的贡献分别相同。
-
白点:
\(w\times C_{n-K-1}^{a-1}\times a!\times b!\times K!\)
-
黑点:
\(w\times C_{K-1}^{x-1}\times x!\times y!\times (n-K)!\)
然后就没有然后了。
ps:取模一定要取彻底。


