关于有向图强连通分量的一点想法
前言
在 20210410 宏帆机房,gm讲强连通分量和缩点的时候,因为大家对于这个知识点的理解和想法不同,产生了激烈的争吵(诡辩)。
本来就很蒻的zyq在听了各位巨佬的讨论后,更加不知所云,以至于露出了这样的表情

(还被gm看见了就很淦)
于是 zyq 在第二天,又打开了强连通分量的 PPT , 然后把代码又打了打,在草稿纸上进行了推算,感觉加深了理解,也有了一些自己的看法和解释,如果又巨佬发现这篇 blog 有什么问题,或者有自己的看法和见解,欢迎评论鸭~
前置芝士
DFS,割点,割边,点双连通块,边双连通块
点双连通块 DFS 代码
//谢谢lym(062)大巨佬帮忙改代码
void dfs(int u, int fa){
low[u] = dfn[u] = ++ cnt;
for(int i = head[u]; i; i = Next[i]){
int v = tail[i];
if(v == fa)continue;
if(!dfn[v]){
q.push(make_pair(u, v));
dfs(v, u);
low[u] = min(low[u], low[v]);
if(dfn[u] <= low[v]){
cntcnt ++;
do{
flagf = q.top();
if(flagf.first > flagf.second)
swap(flagf.first, flagf.second);
q.pop();
gb[cntcnt].push_back(flagf);
}
while(flagf.first != u || flagf.second != v);
}
}
else{
low[u] = min(low[u], dfn[v]);
if(dfn[v] < dfn[u]){
q.push(make_pair(u, v));
}
}
}
}
边双连通块 DFS 代码
void dfs(int u, int fa){
low[u] = dfn[u] = ++ cnt;
s.push(u);
for(int i = head[u]; i; i = Next[i]){
int v = tail[i];
if(v == fa)continue;
if(!dfn[v]){
dfs(v, u);
low[u] = min(low[u], low[v]);
if(dfn[u] < low[v]){
bridge[i] = bridge[i ^ 1] = 1;
}
}
else{
low[u] = min(low[u], dfn[v]);
}
}
if(dfn[u] == low[u]){
cntans ++;
++ cntnum;
int flag;
do{
flag = s.top();
s.pop();
block[flag] = cntnum;
}
while(flag != u);
}
}
强连通分量
关于边
在 gm 的 PPT 开头放了这样一张图,其中将遍历 \(e(u, v)\) (表示从 \(u\) 到 \(v\) 的一条有向边)时,\(dfn(v) \ne 0\) 的情况分类讨论并下了定义
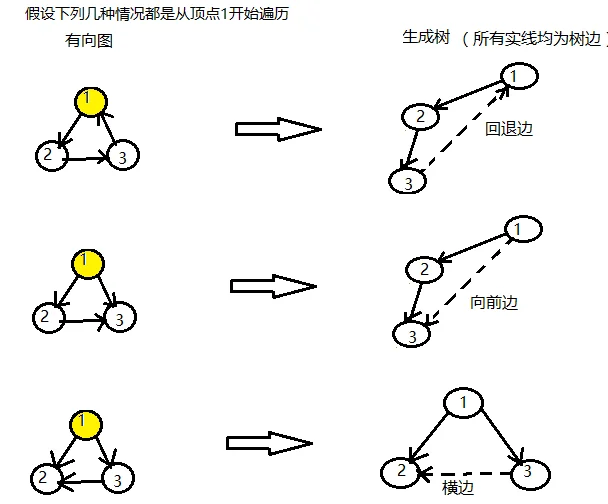
- 那么,在这三种情况当中有且只有回退边会形成环
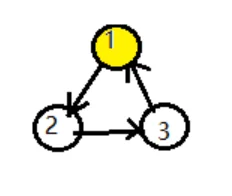
-
而向前边,重复访问了 \(u\) 结点的某个子孙,更新值没有意义,对于该结点的讨论已经在之前完成。
但是在后文的代码中,在
dfn[v] != 0的时候,直接对于block[v] != 0进行了low[u] = min(low[u], dfn[v]);这又是为何呢? 因为子孙的dfn值是不可能大于\(u\),故无需分类讨论,直接比min即可。 -
对于横插边
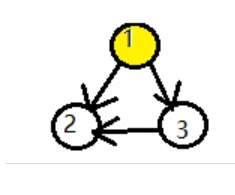
\(u\) 结点和 \(v\) 结点,两结点互无关系,两节点不可能在同一环内,也无法从 \(v\) 遍历到 \(u\)
证明:如果可以从 \(v\) 遍历到 \(u\) , 那么 \(v\) 结点一定是
u结点的祖先,与两结点互无关系相违背。所以两个结点并不处于同一强连通子图。
关于 low 值的定义和解释
在听完各位巨佬的争辩后,蒟蒻 zyq 对于 low 值的定义一头雾水,虽然现在基本忘记了各位巨佬在争什么了
在 gm 的 ppt 上对于 low 值的定义是这样的
从本质上讲,low参数是用来告诉我们从u出发,能形成环的“最高辈份”祖先结点是谁。
个人觉得:即使在有向图中,加入了上面的三种边的概念后依旧是没有问题的。
- 对于回退边 \(v\) 本来就是 \(u\) 的祖先 'low[u] = min(low[u], dfn[v]);' 没有问题
- 对于向前边,前文已经解释了
low[u] = min(low[u], dfn[v]);并不会更新准确的值,只是一个简化的写法。 - 对于横插边,因为'v' 与 'u' 没有关系,所以只需要在特判排除。又因为两个点不在同一棵子树中,两点不可能有环,也不可能在同一强连通子图中,只需要
if(!block[v])判断即可。
所以 zyq 上课的时候为什么会对 low值产生疑问,可能跟 zyq 是个大SB 有关
最后贴上一道 “很板” 的强连通分量 + 缩点的代码
「USACO 2003 Fall」受欢迎的牛
#include <stack>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1e4 + 5;
const int maxm = 1e5 + 5;
int n, m;
int head[maxn], tail[maxm], Next[maxm];
int tot = 1;
int low[maxn], dfn[maxn];
int cnt;
bool vis[maxn];
int cntnum;
int block[maxn];
int head2[maxn], tail2[maxm], Next2[maxm];
bool ib[maxn]; //is begin
bool vvis[maxn][maxn];
stack<int> s;
void add(int x, int y){
tot ++;
tail[tot] = y;
Next[tot] = head[x];
head[x] = tot;
}
void add2(int x, int y){
tot ++;
tail2[tot] = y;
Next2[tot] = head2[x];
head2[x] = tot;
}
void dfs(int u, int fa){
low[u] = dfn[u] = ++cnt;
s.push(u);
vis[u] = 1;
for(int i = head[u]; i; i = Next[i]){
int v = tail[i];
if(!dfn[v]){ //这个子节点没有访问
dfs(v, u);
low[u] = min(low[u], low[v]); //回溯
}
else if(!block[v]){ //这个结点没有被分入任意一个强连通子图
low[u] = min(low[u], dfn[v]);
}
}
if(low[u] == dfn[u]){
cntnum ++;
int x;
do{
x = s.top();
s.pop();
block[x] = cntnum;
}
while(x != u);
}
}
int main() {
scanf("%d %d", &n, &m);
int x, y;
for(int i = 1; i <= m; i ++){
scanf("%d %d", &x, &y);
ib[x] = 1; //可以从这个点出发至其他点
add(x, y);
}
for(int i = 1; i <= n; i ++){
if(!dfn[i] && ib[i]){
dfs(i, 0);
}
}
tot = 0;
for(int i = 1; i <= n; i ++){
for(int j = head[i]; j; j = Next[j]){
int v = tail[j];
if(block[v] == block[i] || vvis[block[i]][block[v]])continue;
add2(block[i], block[v]);
vvis[block[i]][block[v]] = 1;
}
}
for(int i = 1; i <= n; i ++){
if(!dfn[i]){ //在所有点都遍历完成后,依旧没有遍历到,说明这个点与其它任何点都没有连接
printf("0");
return 0;
}
}
int sum = 0;
int side = 0;
for(int i = 1; i <= cntnum; i ++){
if(!head2[i]){
sum ++;
side = i;
}
}
int ans = 0;
if(sum != 1){
printf("0");
return 0;
}
for(int i = 1; i <= n; i ++){
if(block[i] == side){
ans ++;
}
}
printf("%d", ans);
return 0;
}
结语
笔者已经家长叫笔者搞 whk 的声音了,可能明天会做一些没有那么板的题,886~


