1-算法 - 迷宫问题
about
Python3.9
迷宫问题是一个经典的算法问题。问题描述如下:
给一个二维列表,表示迷宫(0表示通道,1表示围墙),给出算法,求一条走出迷宫的路径。
maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
]
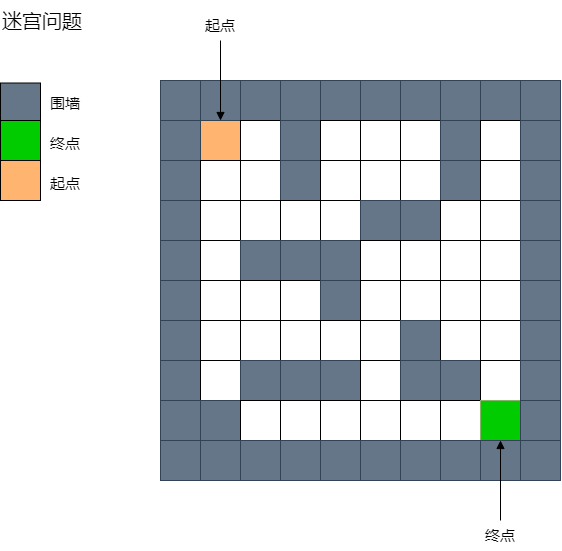
接替方案可以有两种:
- 基于栈解题。
- 基于队列解题。
栈——深度优先搜索
基于栈实现的思路是:从起点所在的节点开始,找下一个(上下左右节点)能走的节点,当找到不能走的节点时(遇到墙或者节点已经走过),退回上一个节点寻找其他方向的能走的节点。
- 将走过的节点入栈,并且标记该节点已经走过。
- 如果当前节点的上下左右四个方向都不能走,就退回到上一个节点继续寻找....直到栈空,表示起点到终点之间没有通路。
- 关键点:
- 上下左右四个方向的坐标点如何获取?
- 如何处理没有通路的情况?
- 怎样才算找到终点?
- 找到的通路是最优(短)的通路吗?
上代码:
maze = [
# 0 1 2 3 4 5 6 7 8 9
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], # 0
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1], # 1
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1], # 2
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1], # 3
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1], # 4
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1], # 5
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1], # 6
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1], # 7
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1], # 8
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], # 9
]
def maze_path_stack(start_x, start_y, end_x, end_y):
"""
栈解决迷宫问题
:param start_x: 起点的x坐标
:param start_y: 起点的y坐标
:param end_x: 终点的x坐标
:param end_y: 终点的y坐标
:return: 找到通路返回True,否则返回False
"""
# 计算当前节点的下一个节点坐标,每次找下一个节点就按照 上下左右 的顺序找,且根据上下左右的顺序不同,最终的路径也会有所不同
direction_list = [
lambda x, y: (x - 1, y), # 上
lambda x, y: (x + 1, y), # 下
lambda x, y: (x, y - 1), # 左
lambda x, y: (x, y + 1), # 右
]
# 定义一个栈
stack = []
stack.append((start_x, start_y)) # 首先将起点坐标入栈,表示从起点开始找下个节点
maze[start_x][start_y] = 2 # 将起点首先标记为已经走过
while stack: # 栈空表示没有通路
current_node = stack[-1] # 取栈顶节点
# 如果当前节点坐标等于终点坐标,就表示已经找到通路了
if current_node[0] == end_x and current_node[1] == end_y:
# 栈内的各个坐标点就是起点找终点的路径
for path in stack: # 这个时候,就直接输出各个路径就完了
print(path)
return True
for d in direction_list:
next_node = d(current_node[0], current_node[1]) # 获取下一个节点的坐标
if maze[next_node[0]][next_node[1]] == 0: # 如果下一个节点是0,表示可以走
stack.append(next_node) # 将下一个节点入栈
maze[next_node[0]][next_node[1]] = 2 # 2用于标记该节点已经走过
break
else: # 如果下个节点(四个方向都找了)不能走,就退回到上一个节点,当然,也要把当前节点标记为已经走过
maze[next_node[0]][next_node[1]] = 2 # 2用于标记该节点已经走过
stack.pop() # 当前节点出栈后,栈顶元素是上一个节点坐标
else: # 如果栈空了,表示起点和终点之间没有通路
return False
maze_path_stack(1, 1, 8, 8) # 1,1 是起点; 8,8 是终点
"""最终的路径
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(5, 2)
(5, 3)
(6, 3)
(6, 4)
(6, 5)
(5, 5)
(4, 5)
(4, 6)
(5, 6)
(5, 7)
(4, 7)
(3, 7)
(3, 8)
(4, 8)
(5, 8)
(6, 8)
(7, 8)
(8, 8)
"""
如果你顺着输出结果捋一遍,发现得到的路径并不是最短的路径。这跟定义的下一个节点的四个方向的先后顺序有关,也跟这个算法的性质有关,基于栈实现的思想是深度优先搜索,也就是一条路走到黑。
那么有最短路径的实现么?答案是基于队列实现。
队列——广度优先搜索
基于队列的实现思路是:从起点所在的节点开始,寻找所有接下来能继续走的点,然后不断寻找,直到直到出路。
队列存储的是当前正在考虑的节点。
from collections import deque
maze = [
# 0 1 2 3 4 5 6 7 8 9
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], # 0
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1], # 1
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1], # 2
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1], # 3
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1], # 4
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1], # 5
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1], # 6
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1], # 7
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1], # 8
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], # 9
]
def output(tmp_list):
""" 处理临时列表,输出起点到终点的路径 """
print(
tmp_list) # [(1, 1, None), (2, 1, 0), (1, 2, 0), (1, 1, 1), (3, 1, 1), (2, 2, 1), (4, 1, 4), (3, 2, 4), (5, 1, 6), (3, 3, 7), (6, 1, 8), (5, 2, 8), (3, 4, 9), (7, 1, 10), (5, 3, 11), (2, 4, 12), (6, 3, 14), (1, 4, 15), (2, 5, 15), (6, 4, 16), (1, 5, 17), (2, 6, 18), (6, 5, 19), (1, 6, 20), (5, 5, 22), (7, 5, 22), (4, 5, 24), (5, 6, 24), (8, 5, 25), (4, 6, 26), (5, 7, 27), (8, 4, 28), (8, 6, 28), (4, 7, 29), (6, 7, 30), (5, 8, 30), (8, 3, 31), (8, 7, 32), (3, 7, 33), (4, 8, 33), (6, 8, 34), (8, 2, 36), (8, 8, 37)]
real_path = [] # 临时列表的路径需要处理,所以,real_path就是处理后的路径
current_node = tmp_list[-1]
while current_node[2] != None: # 因为起点没有上一个节点,所以,之前我们标记为None,这里遇到None就表示可以结束循环了
real_path.append(current_node[0:2]) # 将真实的节点坐标添加到real_path中
current_node = tmp_list[current_node[2]] # 找当前节点的上一个节点
real_path.append(current_node[0:2]) # 最后将起点添加到real_path中
# real_path存储的是从重点找回起点的坐标,而我们要的是从起点到终点的坐标,所以要饭转一下
print(
real_path) # [(8, 8), (8, 7), (8, 6), (8, 5), (7, 5), (6, 5), (6, 4), (6, 3), (5, 3), (5, 2), (5, 1), (4, 1), (3, 1), (2, 1), (1, 1)]
real_path.reverse()
for node in real_path:
print(node)
def maze_path_queue(start_x, start_y, end_x, end_y):
"""
栈解决迷宫问题
:param start_x: 起点的x坐标
:param start_y: 起点的y坐标
:param end_x: 终点的x坐标
:param end_y: 终点的y坐标
:return: 找到通路返回True,否则返回False
"""
# 计算当前节点的下一个节点坐标,每次找下一个节点就按照 上下左右 的顺序找,且根据上下左右的顺序不同,最终的路径也会有所不同
direction_list = [
lambda x, y: (x - 1, y), # 上
lambda x, y: (x + 1, y), # 下
lambda x, y: (x, y - 1), # 左
lambda x, y: (x, y + 1), # 右
]
# 定义一个队列,用来存储正在走的节点
q = deque()
# 定义一个列表,用来存储已经走过的节点
tmp_list = []
# 将起点坐标首先放到队列中, 第三个参数表示当前节点来自于哪个坐标点,由于这里是起点,所以标记为None
q.append((start_x, start_y, None))
while q: # 队列不为空表示有通路
# 获取当前坐标
current_node = q.popleft() # 从右边进(append),从左边出,这是单向队列,如果q.pop(),就是从右边进从右边出,这是栈了
tmp_list.append(current_node) # 将走过的节点放到临时列表中
# 如果当前节点坐标等于终点坐标,就表示已经找到通路了
if current_node[0] == end_x and current_node[1] == end_y:
# 临时列表中的各个坐标点就是起点找终点的路径
output(tmp_list)
return True
for d in direction_list: # 循环获取下个节点的上下左右的坐标
next_node = d(current_node[0], current_node[1])
if maze[next_node[0]][next_node[1]] == 0: # 如果下一个节点是0,表示可以走
# 将可以走的节点入队列,第三个参数是next_node节点来自于哪个节点,这个节点上面我们追加进tmp_list中了
q.append((next_node[0], next_node[1], len(tmp_list) - 1))
maze[next_node[0]][next_node[1]] = 2 # 2用于标记该节点已经走过
else:
return False
maze_path_queue(1, 1, 8, 8)
"""
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(5, 2)
(5, 3)
(6, 3)
(6, 4)
(6, 5)
(7, 5)
(8, 5)
(8, 6)
(8, 7)
(8, 8)
"""
基于队列找到的路径一定是最短路径。但理解起来稍难!!!!
迷宫问题的相关面试题
基于迷宫问题引申出了其他面试题。
找出路
如下maze是一个简易迷宫,1为墙,0为通路,玩家为 %
请写出一个方法,找出走出迷宫的路径,并将路径上的 0 设置为 # ,然后输出修改后的迷宫。
maze = [
[1, 1, 1, 1, 1, 1, 0, 1, 1, 1],
[1, 0, 1, 1, 1, 1, 0, 1, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 1, 0, 1],
[1, 0, 1, 0, 1, 0, 1, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 0, 0, 1, 1],
[1, 0, 1, 1, 0, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 0, 1, 0, 0, 0, 1],
[1, 1, 0, 1, 0, 1, 0, 1, 0, 1],
[1, 0, %, 0, 0, 1, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
]
这里我选择用队列实现:
from collections import deque
maze = [
[1, 1, 1, 1, 1, 1, 0, 1, 1, 1],
[1, 0, 1, 1, 1, 1, 0, 1, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 1, 0, 1],
[1, 0, 1, 0, 1, 0, 1, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 0, 0, 1, 1],
[1, 0, 1, 1, 0, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 0, 1, 0, 0, 0, 1],
[1, 1, 0, 1, 0, 1, 0, 1, 0, 1],
[1, 0, "%", 0, 0, 1, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
]
def output(tmp_list):
""" 处理临时列表,输出起点到终点的路径 """
real_path = [] # 临时列表的路径需要处理,所以,real_path就是处理后的路径
current_node = tmp_list[-1]
while current_node[2] != None: # 因为起点没有上一个节点,所以,之前我们标记为None,这里遇到None就表示可以结束循环了
real_path.append(current_node[0:2]) # 将真实的节点坐标添加到real_path中
current_node = tmp_list[current_node[2]] # 找当前节点的上一个节点
real_path.append(current_node[0:2]) # 最后将起点添加到real_path中
# maze[current_node[0]][current_node[1]] = "%"
real_path.reverse()
for path in real_path:
maze[path[0]][path[1]] = 8 # 为了展示效果考虑,我这里将走过的路标记为8
for i in maze: # 输出结果
print(i)
def maze_path_queue(start_x, start_y, end_x, end_y):
"""
栈解决迷宫问题
:param start_x: 起点的x坐标
:param start_y: 起点的y坐标
:param end_x: 终点的x坐标
:param end_y: 终点的y坐标
:return: 找到通路返回True,否则返回False
"""
# 计算当前节点的下一个节点坐标,每次找下一个节点就按照 上下左右 的顺序找,且根据上下左右的顺序不同,最终的路径也会有所不同
direction_list = [
lambda x, y: (x - 1, y), # 上
lambda x, y: (x + 1, y), # 下
lambda x, y: (x, y - 1), # 左
lambda x, y: (x, y + 1), # 右
]
# 定义一个队列,用来存储正在走的节点
q = deque()
# 定义一个列表,用来存储已经走过的节点
tmp_list = []
# 将起点坐标首先放到队列中, 第三个参数表示当前节点来自于哪个坐标点,由于这里是起点,所以标记为None
q.append((start_x, start_y, None))
while q: # 队列不为空表示有通路
# 获取当前坐标
current_node = q.popleft() # 从右边进(append),从左边出,这是单向队列,如果q.pop(),就是从右边进从右边出,这是栈了
tmp_list.append(current_node) # 将走过的节点放到临时列表中
# 如果当前节点坐标等于终点坐标,就表示已经找到通路了
if current_node[0] == end_x and current_node[1] == end_y:
# 临时列表中的各个坐标点就是起点找终点的路径
output(tmp_list)
return True
for d in direction_list: # 循环获取下个节点的上下左右的坐标
next_node = d(current_node[0], current_node[1])
if maze[next_node[0]][next_node[1]] == 0: # 如果下一个节点是0,表示可以走
# 将可以走的节点入队列,第三个参数是next_node节点来自于哪个节点,这个节点上面我们追加进tmp_list中了
q.append((next_node[0], next_node[1], len(tmp_list) - 1))
maze[next_node[0]][next_node[1]] = 2 # 2用于标记该节点已经走过
else:
print('没有出路')
return False
maze_path_queue(8, 2, 0, 6)
"""
[1, 1, 1, 1, 1, 1, 8, 1, 1, 1]
[1, 2, 1, 1, 1, 1, 8, 1, 0, 1]
[1, 2, 2, 2, 1, 8, 8, 1, 2, 1]
[1, 2, 1, 2, 1, 8, 1, 2, 2, 1]
[1, 2, 1, 2, 8, 8, 2, 2, 1, 1]
[1, 0, 1, 1, 8, 1, 2, 1, 1, 1]
[1, 1, 1, 1, 8, 1, 2, 2, 2, 1]
[1, 1, 2, 1, 8, 1, 2, 1, 0, 1]
[1, 2, 8, 8, 8, 1, 2, 0, 0, 1]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
"""
连锁挖矿
假如要在Minecraft(我的世界)里实现一种连锁挖矿功能,随机生成一个矩阵:0、1、2代表不同的方块类型。
连锁挖矿:破坏一个方块后,接连破坏所有邻接的相同方块。
请完善下方的destroy函数,将破坏的方块改为#,并输出修改后的矩阵。
示例:
import random
size = 8
blocks = [[0 for j in range(size)] for i in range(size)]
# 随机生成一个二维数组来表示矿物随机分布
for x in range(size):
for y in range(size):
blocks[x][y] = random.choice([0, 1, 2])
# 请完善这个destroy函数, 破坏的坐标 x,y | 存储方块类型的矩阵 lists
def destroy(x, y, lists):
...
print(lists)
使用栈来解决问题:
import random
from copy import deepcopy
size = 8
# 随机生成 8*8 矩阵
# lists = [[random.choice([0, 1, 2]) for j in range(size)] for i in range(size)]
lists = [
# 0 1 2 3 4 5 6 7
[0, 0, 1, 2, 0, 2, 0, 0], # 0
[1, 0, 1, 2, 1, 2, 0, 1], # 1
[1, 1, 2, 0, 0, 2, 1, 0], # 2
[1, 1, 0, 2, 0, 0, 0, 0], # 3
[2, 2, 0, 1, 0, 2, 1, 2], # 4
[0, 2, 0, 0, 2, 2, 2, 1], # 5
[0, 0, 1, 2, 2, 2, 0, 2], # 6
[0, 1, 1, 1, 2, 0, 0, 0] # 7
]
"""
根据当前坐标,获取上下左右的坐标点,如坐标:(6, 5) x, y 那么,它的上下左右的坐标点:
上:x-1,y;下:x+1,y;左:x,y-1;右:x,y+1
"""
direction_list = [
lambda x, y: (x + 1, y),
lambda x, y: (x - 1, y),
lambda x, y: (x, y - 1),
lambda x, y: (x, y + 1)
]
def destroy(x, y, lists, sign):
"""
:param x: 顶级列表索引下表 符号
:param y: 子列表中元素的下标
:param x,y: 二维列表中的元素坐标
:param lists: 二维数组
:param sign: 符合条件的坐标替换为指定的字符样式
:return: 返回修改后的二维列表
"""
new_lists = deepcopy(lists)
stack = []
coordinate = new_lists[x][y] # 指定坐标位置的元素
new_lists[x][y] = sign # 起点位置的坐标节点也需要替换
print('坐标({},{}): {}'.format(x, y, coordinate))
stack.append((x, y)) # 起点坐标,也就是给定的坐标位置
while len(stack) > 0: # 当栈为空表示全部替换完毕
current_node = stack[-1] # 栈顶的坐标,也就是当前所在的坐标节点
for direction in direction_list: # 循环获取当前坐标的上下左右坐标点
next_node = direction(current_node[0], current_node[1]) # 下一个坐标
tmp_index = len(new_lists) - 1
if 0 <= next_node[0] <= tmp_index and 0 <= next_node[1] <= tmp_index: # 上下左右的坐标不允许超出列表的索引范围
if new_lists[next_node[0]][next_node[1]] == coordinate: # 下一个坐标需要替换的话
stack.append((next_node[0], next_node[1])) # 将next node坐标点入栈,后续该坐标就会成为current node,在此基础上找上下左右节点
new_lists[next_node[0]][next_node[1]] = sign # 将下一个坐标替换为指定字符
break # 结束标记、入栈、替换任务
else: # 如果当前坐标节点的上下左右坐标点都不需要替换,就回退到上一个节点
stack.pop()
# 下面是为了方便观察结果做的打印操作
print('原二维数组:\n', '\n'.join(str(i) for i in lists))
print('修改后的二维数组:\n', '\n'.join(str(i) for i in new_lists))
return new_lists
destroy(3, 4, lists, '🚩')
destroy(2, 2, lists, '🚩')
destroy(0, 0, lists, '🚩')
destroy(6, 5, lists, '🚩')
destroy(7, 0, lists, '🚩')
"""
坐标(3,4): 0
原二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, 2, 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, 2, 1, 2]
[0, 2, 0, 0, 2, 2, 2, 1]
[0, 0, 1, 2, 2, 2, 0, 2]
[0, 1, 1, 1, 2, 0, 0, 0]
修改后的二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, 2, '🚩', '🚩', 2, 1, '🚩']
[1, 1, 0, 2, '🚩', '🚩', '🚩', '🚩']
[2, 2, 0, 1, '🚩', 2, 1, 2]
[0, 2, 0, 0, 2, 2, 2, 1]
[0, 0, 1, 2, 2, 2, 0, 2]
[0, 1, 1, 1, 2, 0, 0, 0]
坐标(2,2): 2
原二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, 2, 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, 2, 1, 2]
[0, 2, 0, 0, 2, 2, 2, 1]
[0, 0, 1, 2, 2, 2, 0, 2]
[0, 1, 1, 1, 2, 0, 0, 0]
修改后的二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, '🚩', 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, 2, 1, 2]
[0, 2, 0, 0, 2, 2, 2, 1]
[0, 0, 1, 2, 2, 2, 0, 2]
[0, 1, 1, 1, 2, 0, 0, 0]
坐标(0,0): 0
原二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, 2, 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, 2, 1, 2]
[0, 2, 0, 0, 2, 2, 2, 1]
[0, 0, 1, 2, 2, 2, 0, 2]
[0, 1, 1, 1, 2, 0, 0, 0]
修改后的二维数组:
['🚩', '🚩', 1, 2, 0, 2, 0, 0]
[1, '🚩', 1, 2, 1, 2, 0, 1]
[1, 1, 2, 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, 2, 1, 2]
[0, 2, 0, 0, 2, 2, 2, 1]
[0, 0, 1, 2, 2, 2, 0, 2]
[0, 1, 1, 1, 2, 0, 0, 0]
坐标(6,5): 2
原二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, 2, 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, 2, 1, 2]
[0, 2, 0, 0, 2, 2, 2, 1]
[0, 0, 1, 2, 2, 2, 0, 2]
[0, 1, 1, 1, 2, 0, 0, 0]
修改后的二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, 2, 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, '🚩', 1, 2]
[0, 2, 0, 0, '🚩', '🚩', '🚩', 1]
[0, 0, 1, '🚩', '🚩', '🚩', 0, 2]
[0, 1, 1, 1, '🚩', 0, 0, 0]
坐标(7,0): 0
原二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, 2, 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, 2, 1, 2]
[0, 2, 0, 0, 2, 2, 2, 1]
[0, 0, 1, 2, 2, 2, 0, 2]
[0, 1, 1, 1, 2, 0, 0, 0]
修改后的二维数组:
[0, 0, 1, 2, 0, 2, 0, 0]
[1, 0, 1, 2, 1, 2, 0, 1]
[1, 1, 2, 0, 0, 2, 1, 0]
[1, 1, 0, 2, 0, 0, 0, 0]
[2, 2, 0, 1, 0, 2, 1, 2]
['🚩', 2, 0, 0, 2, 2, 2, 1]
['🚩', '🚩', 1, 2, 2, 2, 0, 2]
['🚩', 1, 1, 1, 2, 0, 0, 0]
"""
that's all


 浙公网安备 33010602011771号
浙公网安备 33010602011771号