1-Python - 基础数据类型
前言
Python 3.x中基础数据类型共分为4种:
- 整型(int)
- 浮点型(float)
- 复数(complex)
- 布尔型(bool)
你要问不是还有长整型(long)么?注意,长整型在Python 3.x中统一归为整形了。
整型:int
整型数就是不包括小数部分的数值,分为整数、0和负数,Python提供了int用于表示现实中的整数。
Python为int类型提供了数学运算及运算符。
>>> 2+4*2
10
>>> 2*4/4
2.0
>>> 4/2
2.0
>>> type(4*2)
<class 'int'>
>>> type(4/2)
<class 'float'>
由上例可以看出,运算规则与数学运算规则基本一致,只是在除法“/”时,返回的是float类型,如果想要实现复杂的计算,可以加括号,跟数学计算一样。
>>> ((2+4) * 3 / (3 + 2)) + 2 * 3
9.6
int类型不仅能与算数运算符结合,还能跟赋值运算符结合。
>>> x = 5
>>> x += 1
>>> x
6
>>> x -= 1
>>> x
5
>>> x *= 1
>>> x
5
>>> x *= 2
>>> x
10
>>> x /= 1
>>> x
10.0
>>> x /= 2
>>> x
5.0
这里再次说一下赋值运算符,在现实中,我们知道一个数不可能“等于”该数加1,但在编程语言中是一个合法的语句,它的含义是将变量x指向的值加1之后再重新赋值给x本身,鉴于这种操作的频繁,Python包括其他语言提供这种+=的简写形式。
x += 1 # 等价于 x = x + 1
浮点型:float
Python提供了float类型来表示浮点数,float类型的数值与数学中的写法基本一致,但允许小数点后面没有任何数字(小数部分为0),如下列数值都是浮点类型。
3.1415 -6.23 12.0 -5. .5
Python同样为浮点型数值提供了加减乘除等运算,运算符也跟整数类型一样,但有一点,在Python 3.x中,运算符/用于浮点数时,是保留小数部分的,而Python 2.x版本解释器则返回int类型。
>>> 6 / 3
2.0
>>> type(6/3) # Python3.x中
<class 'float'>
>>> type(6/3) # Python2.x中
<class 'int'>
浮点型数据能够表示巨大的数值,能够进行高精度的计算,但由于浮点型数据在计算机内部是用固定长度的二进制表示的,有些数值可能无法精确的表示,只能存储带有微小误差的近似值,比如下面的情况。
>>> 1.2 - 1.0 # 示例1
0.19999999999999996
>>> 2.2 - 1.2 # 示例2
1.0000000000000002
>>> 2.0 - 1.0 # 示例3
1.0
上面的例子可以看到,示例1的结果比0.2略小,而示例2比1.0略大,而示例3则算出了精确的结果,一般而言,这种微小的误差不影响实际应用,但在一些极端情况下,因为极小的误差,仍能导致出错。
>>> 1.2 - 1.0 == 0.2
False
>>> 2.0 - 1.0 == 1.0
True
上面我们用运算符==来比较两个表达式,结果显示为布尔值的True和False,从上面的例子中我们得出了一个重要的经验:不要在浮点数中使用运算符==来判断是否相等,但有较真的就想这么比较怎么办,我们不应该直接比较,而是通过计算两个浮点数的差值是否足够小,是的话,我们认为相等。
>>> epsilon = 0.0000000000001 # 足够小的数
>>> abs((2.2 - 1.2) - 1) <= epsilon
True
>>> abs((1.2 - 1.0) - 0.2) <= epsilon
True
注意,abs()函数返回一个数值的绝对值。
>>> abs(-5)
5
>>> abs(-5.0)
5.0
Python用浮点型数值表示很大或很小的数值时,会自动采用科学计数法来表示。
>>> 1234.56789 ** 10
8.225262591471028e+30
>>> 1234.56789 ** -10
1.2157666565404538e-31
但下面种情况下除外,这种情况Python将长串的数值理解为一串整型数,会原封不动的打印出来。而上面的例子则是计算的结果。
>>> 1111111111111123121213
1111111111111123121213
>>> 123123131313131313131321231321231
123123131313131313131321231321231
>>> type(123123131313131313131321231321231)
<class 'int'>
注意,从运算效率来说,float相对于int运算效率略低。所以,如果不是必须用到小数,一般应该采用整数类型。另外,不要用浮点数来通过运算符==来判断是否相等这样的问题。
那么,我们常用==和is做判断,那么二者是否是一个意思呢?我们就通过来例子来看看==和is 的区别。
>>> a = 256
>>> b = 256
>>> c = 257
>>> d = 257
>>> a == b
True
>>> a is b
True
>>> c == d
True
>>> c is d
False
>>> id(a)
494578096
>>> id(b)
494578096
>>> id(c)
57248800
>>> id(d)
57248784
在解释之前,我们需要补充一点知识,Python为了实现对内存的有效利用,在对小整数-5~256之内的整数会进行缓存,不在此范围内的则不缓存。那么,我们再来说上面的例子,通过各变量在内存中的id看到,a和b都指向同一个内存空间,所以,无论是is还是==都是True,那么我们再来看c和d,在内存中的id地址是不同的,但是两者的值是相同的,那么可以得出,==比较的是值,而is则是比较的是两个变量在内存中的id地址。
布尔类型:bool
上一节中的示例中,判断两个数是否相等时,Python给我们返回了布尔类型的结果,那么什么是布尔类型呢?
布尔是19世纪英国的数学家,他建立了命题代数,所谓的命题就是可以判断命题真假的语句。在编程语言中,将真假两个值组成了一个类型,即布尔类型,真假值也称为布尔值,以真假为值的表达式称为布尔表达式,布尔表达式在程序中的作用是根据条件的真假执行对应的语句。
Python在2.3版本之后就定义了布尔类型bool,bool类型的两个值为True和False。在2.3版本之前,Python用1和0来表示真、假,这个方法沿用至今。
>>> if 1:
... print('true')
... else:
... print('false')
...
true
布尔表达式最常用的是判断两个表达式的数值大小关系的。
[表达式] [运算符] [表达式]
>>> 2 == 2
True
但布尔表达式在判断字符串的时候就不那么简单了。
>>> 'oldboy' == 'oldboy'
True
>>> 'oldboy' == 'OLDBOY'
False
在Python中,字符串是按字典的顺序进行比较的,也就是说是基于字母顺序比较,而字母顺序是按照ASCII编码顺序排列的。所以,不管是大小写字母,标点符号,阿拉伯数字以及各种字符也是要按照ASCII编码来确定大小。
>>> 3 > 3
False
>>> 3 > 2
True
>>> 2 * 2 > 2
True
>>> 'like' > 'lake'
True
那么,我们怎么查看这些数字、字母、标点符号在ASCII编码中的位置大小呢?我们可以通过ord函数来查看。
>>> ord('1')
49
>>> ord('a')
97
>>> ord('A')
65
>>> ord(',')
44
>>> ord('<')
60
ord函数返回字符在ASCII中的位置序号。
当然,仅用简单的布尔表达式不足以满足某些需求,将多个简单的布尔表达式用逻辑运算符连接起来组成复杂的布尔表达式,回顾一下我们学过的逻辑运算符:and、or、not。
[布尔表达式] and [布尔表达式]
[布尔表达式] or [布尔表达式]
not [布尔表达式]
复杂表达式各项的值依赖于参加逻辑运算的布尔表达式的值,具体的依赖关系可以用真值表来定义:
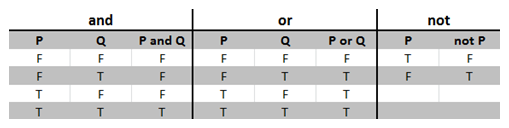
在上图中,P和Q是参加运算的布尔表达式,T和F表示真假值。在and中,P和Q各有两种可能的值,所以P、Q组合共有4中不同的值组合,每种组合在表中一行表示,后面一列是P and Q的值,从表中可知,只有当P、Q都为真,并且P and Q为真,整个表达式为真。
>>> 3 > 3 and 3 < 4
False
>>> 3 > 2 and 3 < 4
True
在or中,只有P or Q为假,且P、Q也为假,表达式为假,也就是说,只要其中一项为真,则表达式为真。
>>> 3 > 3 or 3 < 4
True
>>> 3 > 3 or 3 == 4 or 3 == 3
True
not的用法相对简单。
>>> not 3 > 3
True
>>> not not 3 > 3
False
上例中,not not 3 > 3语句相当于我们生活中的双重否定为肯定。利用这三个逻辑运算符可以构建复杂的布尔型表达式。在复杂的布尔表达式中,同算数运算符一样,谁先谁后计算成了问题,这就要牵扯到运算符的优先级了,回顾一下上一小节中我们列出运算符的优先级的图,可以看到逻辑运算符的优先级。
not > and > or
在此再介绍一种别的语言不支持的表达式形式。
>>> 3 > 2 < 4
True
>>> 3 > 2 < 4 == 4 != 5
True
虽然这在数学中常用,但我们仍不推荐这种方式,因为这不为大多数语言所接受,对于这类表达式,还是用逻辑运算符比较好。
小结:有时候适当的加括号,来改变原有的优先级,就像数学运算中加括号改变计算顺序一样如计算:2 * (2 + 2)。
>>> print( 0 or not 0 or '')
True
>>> print( 0 or not 0 or '' and 1)
True
>>> print( 0 or not 0 or '' and 1 and 0)
True
>>> print( 0 or not 0 or '' and 1 and 0 and None)
True
>>> print( (0 or not 0 or '') and 1 and 0 and None)
0
>>> print( (0 or not 0 or '') and 1 and 0 or None)
None
>>> print( (0 or not 0 or '') and 1 and 0 or None)
None
通过上面的例子,我们可以发现,返回值是有一定的规律的。
如果用x、y表示任何表达式。
x and y
and中,如果x的值为false,则返回x的值,否则返回y的值。
>>> 1 and 0
0
>>> 0 and 1
0
or中,如果x的值为false,则返回y的值,否则返回x的值。
>>> 0 or 1
1
>>> 1 or 0
1
not中,如果x的值为false,则返True,否则返回False。
>>> x = 0
>>> not x
True
>>> y = 1
>>> not y
False
>>> not not y
True
注意:Python中,元素自带布尔值,也就是说,每个元素都有自己的布尔值,我们可以通过bool函数来证明。
>>> bool(0)
False
>>> bool(1)
True
>>> bool(None)
False
>>> bool('')
False
>>> bool([])
False
>>> bool(-1)
True
由上例可以看到,在Python中,0、None、空为假,其余为真。
注意:空包括,空的字符串,空的容器类型。
复数:complex
Python用complex表示复数类型,但由于不常用,我们只做了解。
在数学中,任意数可表示为a + bi,a称为实部,b称为虚部;而Python中complex类型的表示方法为(a + bj)。
注意,Python中的complex类型的虚数符号用j表示,而不是数学中的i,在不会产生误解的情况下,(a + bj)可以省略括号为a + bj。
complex类型也可以执行数学运算。
>>> c1 = 3 + 5j
>>> c2 = 2 + 4j
>>> c1 + c2
(5+9j)
>>> c1 - c2
(1+1j)
>>> c1 * c2
(-14+22j)
>>> c1 ** c2
(-0.5249747542492873+0.16891854983884866j)
>>> abs(c1)
5.830951894845301
需要注意的是,abs函数对复数的计算是返回复数的模数。
我们也可以通过c1.real()和c1.imag()来分别获取c1的实数和虚数,结果都是float类型。
>>> c1 = 3 + 5j
>>> c2 = 2 + 4j
>>> c1.real
3.0
>>> c1.imag
5.0
欢迎斧正,that's all


 浙公网安备 33010602011771号
浙公网安备 33010602011771号