杨表和钩子公式
杨表
杨氏矩阵（Young Tableau），又称杨表，是一类每行长度严格不降的表格，大小为 \(n\)，数字 \(1,2,..,n\) 在表中满足从左到右和从上到下严格递增。设第 \(i\) 行的长度为 \(\lambda_i\)，则 \(\lambda _i\geq \lambda_{i-1},\sum_{i}\lambda_i=n\)，大小为 \(n\) 的杨表形态 \((\lambda_1,\lambda_2,...)\) 与 \(n\) 的整数划分一一对应。
形态为 (5,4,1) 的杨表：
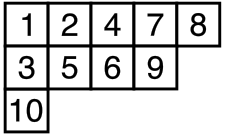
设 \(Y(\lambda)\) 为划分 \(\lambda\) 对应形态的杨表，\(f(\lambda)\) 表示杨表 \(Y(\lambda)\) 中填数的方案数。
设划分 \(\lambda,\mu\) 分别是 \(n,n-1\) 的划分（\(n\geq 2\)），若 \(\exist j,s.t.\forall i\neq j,\lambda_i=\mu_i,\;\;\lambda_j=\mu_i+1\)，记 \(\mu \uparrow \lambda\)。
对于 \((i,j)\in Y(\lambda)\)，记 \(H_{\lambda}(i,j)\) 表示 \((i,j)\) 自身以及下方和右方的格子集合（\(\text{Hook}\)），\(h_{\lambda}(i,j)=|H_{\lambda}(i,j)|\) 。
钩子公式
\(\text{Hook Formula}\)：
\(\text{Proof}\)：
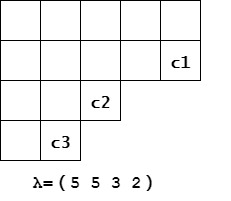
设 \(c_1,c_2,..,c_m\) 为 \(h_{\lambda}(i,j)=1\) 的位置，记 \(\mu_i=\lambda / \{c_i\}\)，显然 \(\{\mu_1,\mu_2,..,\mu_m\}=\{\mu|\mu\uparrow \lambda\}\) 。
\(f(\lambda)\) 满足 \(\displaystyle f(\lambda)=\sum_{\mu\uparrow \lambda}f(\mu)\)，设 \(\displaystyle e(\lambda)=\frac{n!}{\prod_{(i,j)\in Y(\lambda)}h_{\lambda}(i,j)}\)，由于 \(f(\empty)=e(\empty)=1\)：
于是命题转化成证明：\(\displaystyle \sum_{i=1}^m \frac{e(\mu_i)}{e(\lambda)}=1\) 。
定义以下随机游走（\(\text{Hook Walk}\)）：
- 随机选取一个位置 \((i,j)\in Y(\lambda)\) 出发。
- 每次从 \((i,j)\) 等概率地走到 \(H_{\lambda}(i,j)/ \{(i,j)\}\) 中随机一格。
- 若来到某个位置 \(c_i\)，则随机过程结束。
显然 \(\sum_{i=1}^m P(\text{终点为 }c_i)=1\)，下证 \(P(\text{终点为 }c_i)=\frac{e(\mu_i)}{e(\lambda)}\) ：
注意到 \(h_{\lambda}(i,j)+h_\lambda(i+1,j+1)=h_\lambda(i,j+1)+h_\lambda(i+1,j)\)，且只有在 \((i,j)\) 正上方和正右方的位置可以走到 \((i,j)\) 。于是构造二维矩阵 \(\{h_{i,j}\},\{p_{i,j}\}\) ：
\(\text{Lemma}\)：\(\displaystyle \sum_{k=0}^i\sum_{l=0}^j p_{k,l}=\prod_{k=0}^i(1+\frac{1}{h_{k,0}})\prod_{l=0}^j(1+\frac{1}{h_{0,l}})\)
\(\text{Proof}\)：考虑归纳，首先容易验证 \(i,j\in\{0,1\}\) 上式成立。
根据 \(h_{i,j}\) 的递推式，容易得到 \(h_{i,j}=h_{i,0}+h_{0,j}\) 。设 \(S(i,j)=\displaystyle\sum_{k=0}^i\sum_{l=0}^j p_{k,l}\)，对于 \(S(i,0)\)，其值相当于从 \((0,0)\) 出发，每次向下走若格，然后标记一个 \(h_{i,0}\)，由归纳容易得到 \(S(i,0)=\prod_{k=0}^i (1+\frac1{h_{k,0}})\) 以及类似地 \(S(0,j)=\prod_{l=0}^j (1+\frac1{h_{0,l}})\)，两者满足条件。对于当前 \(i,j>0\)，假设 \(S(i-1,j-1),S(i-1,j),S(i,j-1)\) 均满足条件，则
由归纳 \(\text{Lemma}\) 得证。
对应到原问题，对于 \((a,b)\)，令 \(h_{i,0}\) 和 \(h_{0,j}\) 为 \(h_{\lambda}(a\!-\!i,b)-1\) 和 \(h_{\lambda}(a,b\!-\!j)-1\)，则对于任意 \(i,j\geq 0\) 有 \(h_{i,j}=h_{\lambda}(a\!-\!i,b\!-\!j)-1\)，\(p_{i,j}\) 为从 \((a\!-\!i,b\!-\!j)\) 走到 \((a,b)\) 的概率。令 \((a,b)\) 为 \(c_i\) ：
因此 \(\text{Hook Formula}\) 得证。
应用
有一个 \(n\times m\) 的网格，你希望用 \(3-\)连通块（\(\text{triomino}\)） 覆盖整个网格，每个块从 \(1\) 到 \(nm/3\) 标号。对于两个块 \(X,Y\)，若 \(X\) 的某个格子位于 \(Y\) 的一个格子的正左方或正上方，则 \(X\) 的标号需要小于 \(Y\) 。
求带标号的覆盖方案数，模 \(10^9+7\) 。\(1\leq n,m\leq 10^4\)
标号方式使得可能出现两个块的标号关系是自相矛盾的，因此合法的 \(\text{triomino}\) 只有 \(4\) 种：
# ## # ###
# # ##
#
考虑从左上角开始填，使得轮廓线任意时刻都是单调的，即长度为 \(n+m\)，记竖着的线段为 \(1\)，横着的为 \(0\)，则任意时刻的轮廓线都可以表示为长度为 \(n+m\) 的 \(01\) 序列，其中有 \(n\) 个 \(1\) 和 \(m\) 个 \(0\) 。
对于每种合法 \(\text{triomino}\)，加入时对轮廓线产生的变化分别为：1110 -> 0111，1100 -> 0101，1010 -> 0011，1000 -> 0001 。可以发现，无论中间两个值是什么，加入一个 \(\text{triomino}\) 都是将两边的 01 互换。
本来是要 111...11000...0 转变为 000...0111...11，现在能做的操作是将两个相距 \(3\) 格的 01 互换，考虑将序列位置按照 \(\!\!\!\mod 3\) 分开考虑。于是现在有三个 11..10..00，每次可以将相邻的 01 互换，最终变成 0..0011..1，求方案数。
将这个问题往回转，可以发现就是在网格里单调地填方块，方块先后顺序需要满足的约束与杨表相同，因此就是一个矩形杨表计数问题，设矩形为 \(n\times m\)，则方案数为：
设 \(S(n)=\prod_{i=1}^n i!\)，则答案为 \(\displaystyle \frac{(nm)!S(n-1)S(m-1)}{S(n+m-1)}\)，于是预处理阶乘，时间复杂度为 \(O(nm+T)\) 。
