LOJ #6240. 仙人掌

题目链接

LOJ #6240. 仙人掌

题目大意

给定一棵大小为 \(n\) 仙人掌，每条边至多出现在一个环里，求对其随机点分治的期望运行时间。
即将当前连通块的大小累加到 \(cnt\) 中，然后随机选取一个点，将点和与其相连的边删去，得到若干个连通块后递归重复此过程，求 \(cnt\) 的期望值。
\(n\leq 400\)

思路

考虑对每个节点，求出其被删除时所在连通块大小的期望值 \(E(siz_i)\)，则所求期望 \(E(cnt) = \sum E(siz_i)\) 。
连通块的贡献可以拆解为点对的贡献，记 \(P(i,j)\) 表示在删除点 \(i\) 时，存在一条路径连通 \(i,j\) 的概率，则 \(E(siz_i) = \sum_{j=1}^n P(i,j)\) 。
对于仙人掌退化为树的情况，\(i\) 到 \(j\) 之间有唯一的路径，那么在之前的过程中，\(i\) 和 \(j\) 以及中间的路径属于同一个连通块，连通块内选取分治点是随机的，所以 \(i\) 成为路径上第一个被删去的点的概率即 \(\frac{1}{dis(i,j)}\) 。

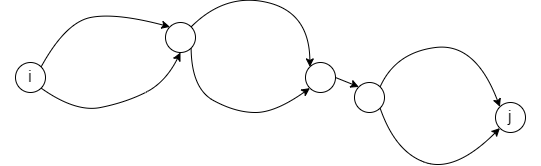
考虑一般仙人掌上情况，点 \(i,j\) 可以由多条路径相连，考虑固定其中一些，剩下的连通性任意，记固定下来的路径的并为 \(A\)，则 \(A\) 的系数为所有并为 \(A\) 的路径集合 \(mask\) 的 \((-1)^{|mask|-1}\) 之和，\(P(i,j)\) 利用 \(A\) 连通的概率即 \(\frac{1}{|A|}\) 。

进一步对 \(A\) 的系数进行容斥，枚举集合 \(B\)，强制所有路径不能经过 \(B\) 中的弧，而注意到若限制 \(B\) 下合法路径存在，则 \(B\) 对应的路径 \(mask\) 系数和为 \(1\)，\(B\) 的权值为 \((-1)^{|B|}\)。记 \(cyc\) 为 \(i\) 到 \(j\) 环的数量，合法的 \(B\) 的个数为 \(3^{cyc}\)，系数和为 \(\sum_{i=0}^{cyc} \binom{cyc}{i}2^i(-1)^i = (-1)^{cyc}(2-1)^{cyc}=(-1)^{cyc}\)，所以 \(A\) 的系数即 \((-1)^{cyc}\) 。

于是考虑对最终剩余点的数量进行 DP，对每个 \(i\) 依次进行：设 \(dp(j,x)\) 表示走到点 \(j\)，除了必经点外 \(A\) 中的节点有 \(x\) 个的方案数，每次经过一个环时，枚举选上弧、下弧还是整个环即可。
DP 可以在圆方树上做，时间复杂度 \(O(n^3)\) 。

Code

#include<iostream>
#include<cstring>
#include<stack>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 404
#define ll long long
#define mod 998244353
using namespace std;

int n, m;
int low[N], dfn[N];
int cnt, num, tot;
stack<int> s;

ll dp[2*N][N], inv[N], ans;

struct Graph{
    int head[2*N], nxt[4*N], to[4*N];
    int deg[2*N], cnt;

    void init(){ mem(head, -1), cnt = -1; }
    void add_e(int a, int b, int id){
        nxt[++cnt] = head[a], head[a] = cnt, to[cnt] = b, deg[a]++;
        if(id) add_e(b, a, 0);
    }
} G, F;

void tarjan(int x){
    dfn[x] = low[x] = ++num;
    s.push(x);

    for(int i = G.head[x], y, z; ~i; i = G.nxt[i])
        if(!dfn[y = G.to[i]]){
            tarjan(y), low[x] = min(low[x], low[y]);
            if(low[y] >= dfn[x]){
                F.add_e(x, ++tot, 1);
                do{
                    z = s.top(), F.add_e(z, tot, 1);
                    s.pop();
                } while(z != y);
            }
        } else low[x] = min(low[x], dfn[y]);
}

void dfs(int x, int fa, int dis, int tot){
    if(x <= n){
        dis++;
        rep(i,0,min(tot, n-dis)) if(dp[x][i] %= mod)
            (ans += inv[dis+i] * dp[x][i]) %= mod;
    }
    int pos = 0;
    if(x > n) for(int i = F.head[x]; ~i && F.to[i] != fa; i = F.nxt[i]) pos++;
    for(int i = F.head[x], it = 0; ~i; i = F.nxt[i], it++){
        int y = F.to[i];
        if(y == fa) continue;
        if(x <= n){
            rep(j,0,tot) dp[y][j] = dp[x][j];
            dfs(y, x, dis, tot);
        } else{
            int l1 = it-pos, l2 = pos-it;
            if(l1 < 0) l1 += F.deg[x]; l1--;
            if(l2 < 0) l2 += F.deg[x]; l2--;
            rep(j,0,tot) if(dp[x][j] %= mod){
                if(j <= n-l1) dp[y][j+l1] += dp[x][j];
                if(j <= n-l2) dp[y][j+l2] += dp[x][j];
                if(j <= n-l1-l2) dp[y][j+l1+l2] += mod - dp[x][j];
            }
            dfs(y, x, dis, tot+l1+l2);
        }
    }
}

int main(){
    cin>>n>>m;
    G.init(), F.init();
    int u, v;
    rep(i,1,m) cin>>u>>v, G.add_e(u, v, 1);

    inv[0] = inv[1] = 1;
    rep(i,2,N-1) inv[i] = (mod-mod/i) * inv[mod%i] % mod;
    tot = n, tarjan(1);
    rep(i,1,n) mem(dp, 0), dp[i][0] = 1, dfs(i, 0, 0, 0);
    cout<< ans <<endl;
    return 0;
}