可持久化数据结构维护路径计数问题
其实就两道比较相关的题目。
Graph Subpaths
给定一张 \(n\) 个节点 \(m\) 条的 \(DAG\),满足每条有向边 \(a\rightarrow b\),\(a<b\) 。另外给出 \(k\) 条 \(DAG\) 上的路径。对于 \(2\leq i\leq n\),求出 \(1\) 到 \(i\) 的路径条数,满足路径不包含给出的 \(k\) 条路径中的任意一条。
\(2\leq n,m\leq 10^5\),\(k\leq 5\times 10^4\),\(k\) 条路径总长度 \(\leq 10^5\)
来源:ByteDance/Moscow Workshops Programming Camp 2020 Online Contest, G
考虑将路径当成字符串来处理,对 \(DAG\) 建立类似 \(Trie\) 的数据结构,记 \(num(i)\) 为节点 \(i\) 答案,对于没有路径限制的情况,每个点将其入边节点的路径数量求和即可。
考虑给定的一条路径带来的影响,假设当前考虑到了路径末端的节点 \(x\),那么在路径上的那个邻居就不能对其产生贡献,实际贡献应来自路径两侧的所有节点。

这里直接做是 \(O(\sum \deg(i))\) 的,显然不能接受。这里的操作相当于路径上点各自扣掉一部分,然后作贡献,不过直接扣掉 \(num(son)\) 显然是不对的,因为路径上的节点可能是其它路径的末尾,之前 \(son\) 对其的贡献就不是 \(num(son)\),而是另一系列路径两侧点。
于是考虑维护可持久化数据结构,我们用可持久化动态开点线段树维护 \(Trie\) 的形态,需要支持的操作有:
- 在特定位置插入一个节点:即 \(x\) 的所有入边节点对其产生贡献。
- 删除一个特定位置的节点:扣掉路径上的儿子。
- 复制一棵线段树:路径上的节点自身不需要这些容斥,容斥是作用于 \(x\) 处的信息的。
于是每次先将 \(x\) 入边节点的贡献统计到 \(x\) 中,对于路径自底向上对线段树进行容斥即可。
时间复杂度 \(O(n\log n)\)
背单词
有一个自动机,可以看做一张 \(n\) 个点 \(m\) 条边的有向图,节点编号为 \(1,2,..,n\),每条边上都标有一个正整数,有一些节点是终止节点。对于一条从 \(1\) 到某个终止节点的路径,把它经过的边的标号依次连接起来,可以得到一个序列,这个序列就是一个单词。
\(Q\) 个询问,每次给出一个 \(k\),求所有单词中字典序第 \(k\) 大的单词长度是多少。
不存在第 \(k\) 大输出 -1,长度是 \(\infty\) 时输出 inf,保证一个节点的所有出边标号不同。
\(2\leq n\leq 10^5,0\leq m\leq 10^5,1\leq q\leq 10^5,1\leq k\leq 10^{18}\)
来源:模拟赛,是 HDOJ5118 GRE Words Once More! 的加强版。
先看 \(DAG\) 上的情况,考虑朴素维护一个数组 \(len[x][k]\),表示从 \(x\) 点出发字典序第 \(k\) 大的单词的长度。那么转移就是将 \(x\) 的所有出边节点的 \(len\) 数组按序合并,然后整体加 \(1\),若 \(x\) 是终止节点那么再在序列头部添加一个 \(0\) 。
虽然 \(len[x]\) 的长度可以达到 \(10^{18}\) 级别,但是其中有大量信息重复来自同一个节点,本质上互异的信息只有 \(O(n)\) 级别。于是考虑可持久化,由于要高效合并两个序列,容易想到可持久化平衡树。
于是每次直接做可持久化平衡树合并即可,同时维护一个子树加的标记,显然当 \(x\) 的平衡树大小超过 \(10^{18}\) 时再后面的信息就不用合并了,平衡树特性可以保证 \(x\) 的树高是 \(O(\log k)\) 的。询问时直接查询对应位置答案即可。
对于图上有环的情况,可以发现若对于某个 \(k\),其单词处于一个环内并至少绕了一圈,那么 \(k\) 往后的所有询问便是一直在此环内绕圈了,于是只需要考虑第一个环。
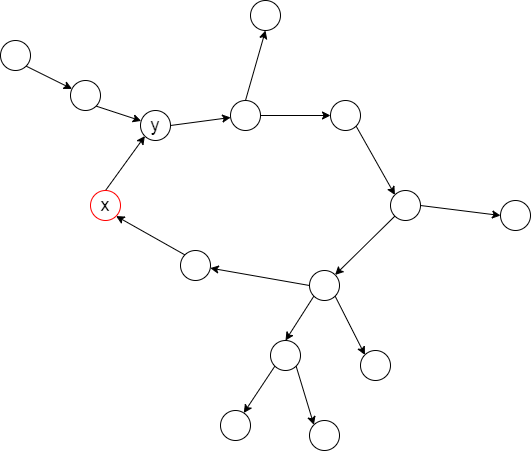
先按照 \(dfs\) 的顺序遍历 照常合并平衡树,然后目前走到了 \(x\) 点,发现 \(y\) 是其 \(dfs\) 树上的祖先,那么现在碰到了第一个环。于是现在 \(x\) 直接退出,因为剩下的路径不可能被遍历到了,\(dfs\) 的过程全部结束。那么这样 \(y\) 的平衡树中储存的就是绕环一圈以内的所有单词信息。
对于一个询问 \(k\),若 \(k\leq\) 节点 \(1\) 的平衡树大小,直接查询答案。否则单词一定绕环了若干圈,记环长为 \(len\),\(y\) 的平衡树的大小为 \(mod\),即一个圈上有 \(mod\) 个单词,那么 \(k\) 对应单词一定绕了 \(\lfloor\frac{k-pre}{mod}\rfloor\) 圈,\(pre\) 是不绕圈的单词数量,即 \(1\) 的平衡树大小,于是将 \(k\) 取模后在 \(y\) 的平衡树上查询答案即可,最后再加上圈数乘环长以及绕圈前的长度(\(1\) 到 \(y\) 的距离)。而若 \(mod=0\),含义就是单词会在环上无休止的绕下去,一旦退出环就会得到更劣的解,所以此时输出 inf 即可。
维护可持久化平衡树(FHQ Treap)有一个细节:合并平衡树不能采用节点的随机权值作为比较,否则在可持久化时,复制出来的树和先前只有根节点权值是不同的,大量相同权值会导致时间复杂度退化到 \(O(nk)\),因此需要在合并时按照两边子树大小随机父子关系。
时间复杂度 \(O(n\log k)\) 。
另解:处理出每个节点可以到达的单词数量,在环上且能到达终止节点即 \(\infty\),类似重链剖分找到重儿子,父亲向重儿子连边得到另一张有向图,走轻边时可达单词数量至少减半,而在重链图上维护 \(k\) 的上下界后可以倍增找到离开的地方。答案上界为 \(nk\),当前计算的值超过上界即对应 inf 。
值域实际为 \(O(2^n)\),但是可以对 \(k\) 取 \(\min\),于是时间复杂度 \(O(n\log k(\log k+\log n))\) 。
Codes
Graph Subpaths
// ByteDance/Moscow Workshops Programming Camp 2020 Online Contest, G
#include<iostream>
#include<vector>
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 101000
#define LOG 18
#define ll long long
#define mod 998244353
using namespace std;
struct Segment_Trie{
struct node{
int ls, rs, node; ll val;
} t[10*N*LOG];
int cnt, root[N];
void insert(int &x, int l, int r, int pos){
if(!x) x = ++cnt;
if(l == r){ t[x].node = root[l], t[x].val = t[root[l]].val; return; }
int mid = (l+r)>>1;
if(mid >= pos) insert(t[x].ls, l, mid, pos);
else insert(t[x].rs, mid+1, r, pos);
t[x].val = (t[t[x].ls].val + t[t[x].rs].val) % mod;
}
void update(int &x, int y, int l, int r, int pos, int v){
x = ++cnt;
if(l == r){ t[x].node = v, t[x].val = t[v].val; return; }
t[x].ls = t[y].ls, t[x].rs = t[y].rs;
int mid = (l+r)>>1;
if(mid >= pos) update(t[x].ls, t[y].ls, l, mid, pos, v);
else update(t[x].rs, t[y].rs, mid+1, r, pos, v);
t[x].val = (t[t[x].ls].val + t[t[x].rs].val) % mod;
}
int get(int x, int l, int r, int pos){
if(l == r) return t[x].node;
int mid = (l+r)>>1;
if(mid >= pos) return get(t[x].ls, l, mid, pos);
else return get(t[x].rs, mid+1, r, pos);
}
} T;
int n, m, k;
vector<int> conn[N], path[N], relate[N];
int main(){
ios::sync_with_stdio(false);
cin>>n>>m;
int u, v;
rep(i,1,m) cin>>u>>v, conn[v].push_back(u);
cin>>k;
rep(i,1,k){
int siz; cin>>siz, path[i].resize(siz);
rep(j,0,siz-1) cin>> path[i][j];
relate[path[i][siz-1]].push_back(i);
}
T.cnt = T.root[1] = 1, T.t[1].val = 1;
rep(cur,2,n){
for(int k : conn[cur]) T.insert(T.root[cur], 1, n, k);
for(int k : relate[cur]){
vector<int> chain = {T.root[cur]};
int siz = path[k].size(), x = 0;
per(i,siz-2,0){
chain.push_back(T.get(chain.back(), 1, n, path[k][i]));
if(chain.back() == 0) break;
}
if(chain.back() == 0) continue;
per(i,siz-2,0) T.update(x, chain[i], 1, n, path[k][siz-i-2], x);
T.root[cur] = x;
}
}
rep(i,2,n) cout<< T.t[T.root[i]].val <<" \n"[i == n];
return 0;
}
背单词 \(O(n\log k)\)
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 101000
#define LOG 65
#define ll long long
#define PII pair<int, int>
#define fr first
#define sc second
using namespace std;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
inline ll rnd(ll l, ll r){ return uniform_int_distribution<ll>(l, r)(rng); }
inline int read(){
int s = 0, w = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){ if(ch == '-') w = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') s = (s<<3)+(s<<1)+(ch^48), ch = getchar();
return s*w;
}
struct Fhq_Treap{
struct node{
int c[2];
ll siz, val, tag;
} t[3*N*LOG];
int cnt;
int New(ll val){
t[++cnt].val = val, t[cnt].siz = 1, t[cnt].c[0] = t[cnt].c[1] = t[cnt].tag = 0;
return cnt;
}
int copy(int x){
if(x == 0) return 0;
t[++cnt].val = t[x].val, t[cnt].siz = t[x].siz, t[cnt].tag = t[x].tag;
rep(i,0,1) t[cnt].c[i] = t[x].c[i];
return cnt;
}
void pushdown(int x){
rep(i,0,1) if(t[x].c[i]){
t[x].c[i] = copy(t[x].c[i]);
t[t[x].c[i]].val += t[x].tag, t[t[x].c[i]].tag += t[x].tag;
}
t[x].tag = 0;
}
void pushup(int x){ t[x].siz = t[t[x].c[0]].siz + t[t[x].c[1]].siz + 1; }
int merge(int x, int y){
if(!x || !y) return x+y;
pushdown(x), pushdown(y);
int z;
if(rnd(0, t[x].siz+t[y].siz) < t[x].siz){
z = copy(x);
t[z].c[1] = merge(t[z].c[1], y);
} else{
z = copy(y);
t[z].c[0] = merge(x, t[z].c[0]);
}
pushup(z);
return z;
}
ll query(int x, ll k){
ll lft = t[t[x].c[0]].siz + 1;
if(k == lft) return t[x].val;
pushdown(x);
return k < lft ? query(t[x].c[0], k) : query(t[x].c[1], k-lft);
}
} T;
int n, m, q;
int s[N], root[N];
vector<PII> son[N]; vector<int> rev[N];
int dep[N], len, st;
bool legal[N], in[N], circ;
void flush(int x){
legal[x] = true;
for(int y : rev[x]) if(!legal[y]) flush(y);
}
void dfs(int x){
in[x] = true;
sort(son[x].begin(), son[x].end());
if(s[x]) root[x] = T.New(0);
for(PII p : son[x]) if(legal[p.sc]){
int y = p.sc;
if(!dep[y]) dep[y] = dep[x] + 1, dfs(y);
if(in[y]){ circ = true, len = dep[x] - dep[y] + 1, st = y; break; }
int z = T.copy(root[y]);
T.t[z].val++, T.t[z].tag++;
root[x] = T.merge(root[x], z);
if(circ || T.t[root[x]].siz > 1e18) break;
}
in[x] = false;
}
int main(){
freopen("c.in", "r", stdin);
freopen("c.out", "w", stdout);
n = read(), m = read(), q = read();
rep(i,2,n) s[i] = read();
int a, b, c;
rep(i,1,m){
a = read(), b = read(), c = read(), son[a].push_back({c, b});
rev[b].push_back(a);
}
rep(i,1,n) if(s[i] && !legal[i]) flush(i);
dep[1] = 1, dfs(1);
ll k, lim = T.t[root[1]].siz, mod = T.t[root[st]].siz;
while(q--){
cin>>k;
if(k <= lim) printf("%lld\n", T.query(root[1], k));
else if(mod == 0) puts(st ? "inf" : "-1");
else{
k -= lim;
__int128 ans = (__int128)len*((k-1)/mod+1) + T.query(root[st], k%mod ? k%mod : mod) + dep[st]-1;
string s = "";
while(ans) s += char(ans%10+'0'), ans /= 10;
reverse(s.begin(), s.end());
for(char c : s) putchar(c);
putchar('\n');
}
}
return 0;
}
背单词 \(O(n\log k(\log k+\log n))\)
#include<iostream>
#include<fstream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<stack>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 210000
#define LOG 80
#define ld long double
#define lll __int128
#define PII pair<int, int>
#define fr first
#define sc second
#define Inf ((ld)1e18)
using namespace std;
int n, m, q, s[N];
vector<PII> son[N];
vector<ld> choice[N];
ld num[N], lb[N][LOG+2], rb[N][LOG+2], k;
int num0, dfn[N], low[N], state[N], up[N][LOG+2];
bool in[N], vis[N];
lll ans;
stack<int> stk;
void dfs0(int x){
low[x] = dfn[x] = ++num0;
state[x] |= s[x], in[x] = true;
stk.push(x);
for(PII p : son[x]){
int y = p.sc;
if(!dfn[y]) dfs0(y), low[x] = min(low[x], low[y]);
else if(in[y]) low[x] = min(low[x], dfn[y]);
state[x] |= state[y];
}
if(dfn[x] == low[x]){
int y;
bool circ = stk.top() != x && state[x]&1;
do{
y = stk.top(); stk.pop();
state[y] |= circ ? 2 | state[x] : 0, in[y] = false;
} while(y != x);
}
}
void dfs(int x){
vis[x] = true;
choice[x] = {num[x] = s[x]};
int hson = 0;
for(PII p : son[x]){
int y = p.sc;
if(!vis[y]) dfs(y);
ld val = state[y] == 3 ? Inf : num[y];
if(val > (state[hson] == 3 ? Inf : num[hson]))
hson = y, lb[x][0] = num[x]+1, rb[x][0] = min(num[x]+val, Inf);
num[x] = min(num[x]+val, Inf), choice[x].push_back(num[x]);
}
if(state[x] == 3) num[x] = Inf;
up[x][0] = hson;
}
void solve(int x, ld k){
if(ans > (__int128)n*::k) return;
if(num[x] < k) return;
lll ret = 1;
if(k >= lb[x][0] && k <= rb[x][0]){
per(i,LOG,0) if(up[x][i] && k >= lb[x][i] && k <= rb[x][i])
k -= lb[x][i]-1, x = up[x][i], ret += (__int128(1))<<(__int128(i));
}
if(s[x] && k == 1){ ans += ret; return; }
int pos = lower_bound(choice[x].begin(), choice[x].end(), k) - choice[x].begin() - 1;
k -= choice[x][pos];
ans += ret;
return solve(son[x][pos].sc, k);
}
int main(){
freopen("c.in", "r", stdin);
freopen("c.out", "w", stdout);
ios::sync_with_stdio(false);
cin>>n>>m>>q;
rep(i,2,n) cin>>s[i];
int a, b, c;
rep(i,1,m) cin>>a>>b>>c, son[a].push_back({c, b});
dfs0(1);
rep(i,1,n){
vector<PII> vec;
for(PII p : son[i]) if(state[p.sc]&1) vec.push_back(p);
son[i] = vec;
sort(son[i].begin(), son[i].end());
}
dfs(1);
rep(i,1,LOG) rep(x,1,n) if(state[x]&1){
if(up[x][i-1]){
up[x][i] = up[up[x][i-1]][i-1];
lb[x][i] = min(lb[x][i-1] - 1 + lb[up[x][i-1]][i-1], Inf);
rb[x][i] = min(lb[x][i-1] - 1 + rb[up[x][i-1]][i-1], Inf);
}
}
rep(i,1,q){
cin>>k, ans = -1, solve(1, k);
if(ans > (__int128)n*k) cout<<"inf\n";
else if(ans == -1) cout<<"-1\n";
else{
string s = "";
while(ans) s += char(ans%10+'0'), ans /= 10;
reverse(s.begin(), s.end());
cout<< s <<endl;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号