LOJ #2564. 「SDOI2018」原题识别

题目链接

LOJ #2564. 「SDOI2018」原题识别

题目大意

一棵 \(n\) 个节点的树，每个节点有一个颜色 \(a_i\) 。有 \(m\) 个询问，两种操作：

• \(\verb!1 x y!\)：求 \(x\) 到 \(y\) 的路径上的颜色数量。
• \(\verb!2 A B!\)：对于所有点对 \((x,y)\)，\(x\) 在 \(1\rightsquigarrow A\) 的路径上，\(y\) 在 \(1\rightsquigarrow B\) 的路径上，求 \(x\) 到 \(y\) 路径颜色种类数之和。

\(2\leq n\leq 10^5,1\leq m\leq 2\times 10^5\)

节点的颜色在 \([1,n]\) 之间随机生成，树的生成方式是：给定参数 \(p\)，\(1,2,..,p\) 是一条链，\(p+1,p+2,..,n\) 随机选取一个比其小的节点作为父亲。

思路

做法参考 出题人题解

首先颜色之间是独立的，于是对于每种颜色分开处理最后求和即为答案。

假设当前考虑的颜色是 \(C\) 。考虑将树上问题转到序列上，求出树的欧拉序（入栈出栈序），记 \(st_x,ed_x\) 为 \(x\) 入栈出栈的时刻，对于 \(x\) 处的某些信息 \(k\)，在 \(st_x\) 处 \(+k\)，\(ed_x\) 处 \(-k\) 。那么一个节点 \(v\) 到根的路径上的信息和即 \(st_v\) 处的前缀和。

建立一个 \(2n\times 2n\) 的矩阵，设 \(u\rightsquigarrow v\) 路径上颜色数为 \(k\)，对矩阵的贡献为 \((st_u,st_v)\) 处 \(+k\)，\((st_u,ed_v)-k\)，\((ed_u,st_v)-k\)，\((ed_u,ed_v)+k\) 。可以发现这样子一个第二类询问 \((x,y)\) 对应的答案就是 \((st_x,st_y)\) 处的二维前缀和。

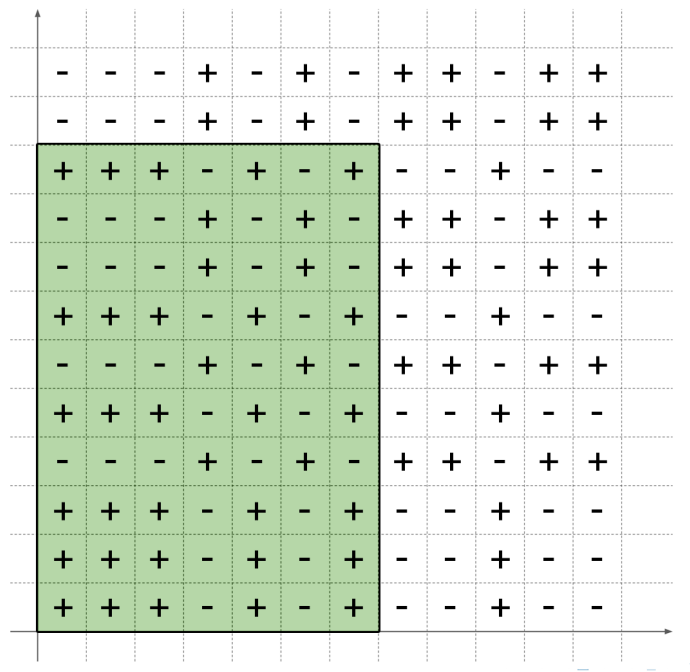
考虑一个 \(color_x=C\) 的节点 \(x\) 会对哪些路径产生贡献：

1. 一个端点在 \(x\) 子树内，另一个任意：\([1,2n]\times [st_x,ed_x]\bigcup [st_x,ed_x]\times [1,2n]\)
2. 两个节点都位于一个 \(x\) 的儿子 \(y\) 的子树内，这是要去掉的：\([st_y,ed_y]\times [st_y,ed_y]\)

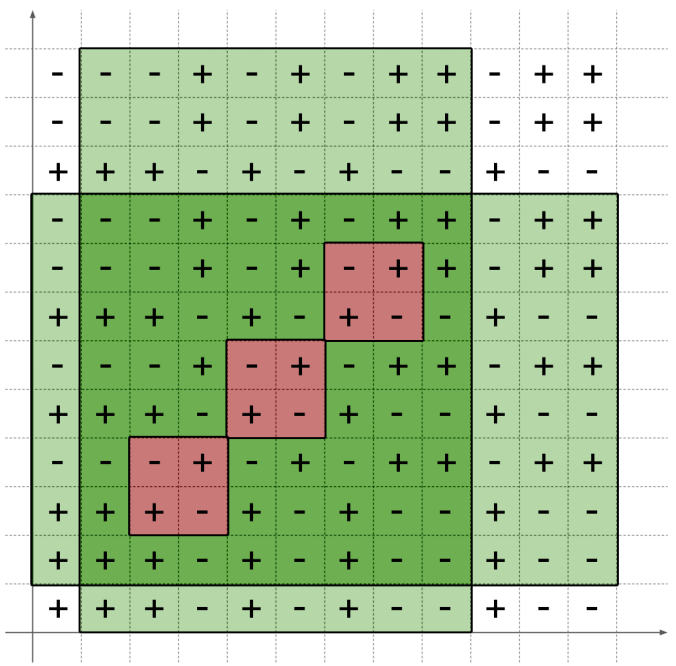
这样便会产生 \(\displaystyle \sum_{color_x=C} (\deg(x)+1)\) 个矩形，第一类矩形贡献为 \(1\)，第二类矩形贡献为 \(-2\)。于是对矩形边界离散化，\(O(n^2)\) 做前缀和得到每个位置的值，若一位置非零，则相当于这里的路径包含颜色 \(C\)，在离散化前对应的区域的 \(k\) 加 \(1\) 。

考虑计算答案，前面对一个矩形区域的 \(k\) 加 \(1\) 也可以二维差分前缀和处理，那么现在考虑每个单点加操作对答案的贡献， \((x,y,p)\) 表示在 \((x,y)\) 处加 \(p\)，对于询问 \((A,B)\) 处的二维前缀和，其答案为

\[\sum_{x_i\leq A,y_i\leq B} (S_A-S_{x_i-1})(S_B-S_{y_i-1})p_i \\ =S_AS_B \sum_i p_i-S_A\sum_{i}S_{y_i-1}p_i-S_B\sum_{i}S_{x_i-1}p_i+\sum_{i}S_{x_i-1}S_{y_i-1}p_i \]

前面说过，对于每个点 \(x\)，\(st_x\) 处信息的权值为 \(1\)，\(ed_x\) 为 \(-1\)，而 \(S_i\) 表示 \(i\) 处权值的前缀和。

容易发现这个式子可以离线，对 \(x_i\) 排序后扫瞄线，用 \(4\) 个树状数组维护 \(4\) 类值的前缀和就可以做到 \(O(n\log n)\) 处理所有询问了。

目前只考虑了操作 \(2\)，而操作 \(1\) 可以简单地看作在 \(2n\times 2n\) 矩阵的上的单点查询，二维前缀和容斥一下就可以转化为若干个操作 \(2\) 。

总共的矩形数量是 \(O(\sum_{x}\deg(x))=O(n)\) 级别的，从而时间复杂度 \(\displaystyle O(n\log n+\sum_C \left(\sum_{color_x=C}\deg(x)\right)^2)\) 。对于后面的式子，当图不是菊花类型的时候表现都是十分优秀的。

时间复杂度

注意到 \(p\) 的取值对时间复杂度没什么影响，于是分析树纯随机的期望复杂度就可以了。

两个节点 \(i,j\) 满足 \(color_i=color_j\) 的概率是 \(\displaystyle\frac{1}{n}\)，\(\displaystyle (\sum_{x\in S} \deg(x))^2=\sum_{x,y\in S} \deg(x)\deg(y)\) ，于是

\[\begin{align} &E\left(\sum_C \left(\sum_{color_x=C}\deg(x)\right)^2\right) \\ =&\frac{1}{n}E\left(\sum_{i\neq j} \deg(i)\deg(j)\right)+E\left(\sum_i \deg(i)^2\right) \\ =&\frac{1}{n}E\left((\sum_i \deg(i))^2-\sum_{i}\deg(i)^2\right)+E\left(\sum_i \deg(i)^2\right) \\ =&\frac{(2n-2)^2}{n}+\frac{n-1}{n}E\left(\sum_i \deg(i)^2\right) \end{align} \]

于是计算 \(E(\sum_i \deg(i)^2)\)：

\[\begin{align} &E\left(\sum_i \deg(i)^2\right) \\ =&n-2+E\left(\sum_{i}(\deg(i)-1)^2\right) \\ =&2n-3+\sum_{i\neq j}\frac{1}{\max(i,j)} \\ =&3n-3-2\sum_{i=1}^{n-1}\frac{1}{i} \\ =&3n-3-O(\ln n)\\ =& O(n) \end{align} \]

从而 \(E\left(\sum_C \left(\sum_{color_x=C}\deg(x)\right)^2\right)\) 是 \(O(n)\) 级别的，此做法的时间复杂度为 \(O(n\log n)\) 。

Code

另外这个题似乎还存在更加优秀的做法，可以线性空间且不依赖随机数据，可惜我不会。

代码有一定的卡常，如合并相同位置的 \((x,y,p)\)，将值域上界设为 \(\max(st_i)\) 而不是 \(2n\)，扫瞄线用基数排序。原题数据 \(T=3\) 的多测 1500ms 左右。

#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<cstdio>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 101000
#define ll long long
#define lowbit(x) (x&-x)
using namespace std;

inline int read(){
    int s = 0, w = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){ if(ch == '-') w = -1; ch = getchar(); }
    while(ch >= '0' && ch <= '9') s = (s<<3)+(s<<1)+(ch^48), ch = getchar();
    return s*w;
}

int n, m, p, Lim, a[N];
int head[N], nxt[2*N], to[2*N];
int dfn[N][2], euler[2*N], S[2*N], s[1000][1000];
int cnt, num;
vector<int> color[N];

struct oper{ int x, y, p; };
struct query{ int a, b, id, k; };
vector<oper> bucket[2*N];
vector<query> Q;
ll ans[2*N];

struct Fenwick{
    ll t[2*N];
    void update(int pos, ll k){
        while(pos <= Lim) t[pos] += k, pos += lowbit(pos);
    }
    ll get(int pos){
        ll ret = 0;
        while(pos) ret += t[pos], pos -= lowbit(pos);
        return ret;
    }
} T0, T1, T2, T3;

void init(){ 
    mem(head, -1), cnt = -1, num = 0;
    mem(T0.t, 0), mem(T1.t, 0), mem(T2.t, 0), mem(T3.t, 0);
    Q.clear();
    rep(i,0,N-1) color[i].clear();
    rep(i,0,2*N-1) bucket[i].clear();
    mem(S, 0), mem(ans, 0);
}
void add_e(int a, int b, bool id){
    nxt[++cnt] = head[a], head[a] = cnt, to[cnt] = b;
    if(id) add_e(b, a, 0);
}

unsigned int SA, SB, SC;
unsigned int rng61(){
    SA ^= SA << 16;
    SA ^= SA >> 5;
    SA ^= SA << 1;
    unsigned int t = SA;
    SA = SB;
    SB = SC;
    SC ^= t ^ SA;
    return SC;
}
void gen(){
    scanf("%d%d%u%u%u", &n, &p, &SA, &SB, &SC);
    for(int i = 2; i <= p; i++)
        add_e(i - 1, i, 1);
    for(int i = p + 1; i <= n; i++)
        add_e(rng61() % (i - 1) + 1, i, 1);
    for(int i = 1; i <= n; i++)
        a[i] = rng61() % n + 1;
}

void dfs(int x, int fa){
    dfn[x][0] = ++num, euler[num] = x, Lim = num+1;
    for(int i = head[x]; ~i; i = nxt[i])
        if(to[i] != fa) dfs(to[i], x);
    dfn[x][1] = ++num, euler[num] = x;
}

vector<oper> work(int c){
    vector<oper> vec;
    auto insert = [&](int a, int b, int c, int d, int k){
        c = min(c, Lim-1), d = min(d, Lim-1);
        vec.push_back({a, b, k});
        vec.push_back({a, d+1, -k});
        vec.push_back({c+1, b, -k});
        vec.push_back({c+1, d+1, k});
    };
    for(int i : color[c]){
        insert(1, dfn[i][0], Lim, dfn[i][1], 1), insert(dfn[i][0], 1, dfn[i][1], Lim, 1);
        for(int j = head[i]; ~j; j = nxt[j]) 
            if(dfn[to[j]][0] > dfn[i][0]) 
                insert(dfn[to[j]][0], dfn[to[j]][0], dfn[to[j]][1], dfn[to[j]][1], -2);
    }

    vector<int> val;
    for(oper op : vec) val.push_back(op.x);
    sort(val.begin(), val.end());
    val.erase(unique(val.begin(), val.end()), val.end());
    int szx = val.size();

    rep(i,0,szx-1) rep(j,0,szx-1) s[i][j] = 0;
    for(oper op : vec)
        s[lower_bound(val.begin(), val.end(), op.x) - val.begin()]
         [lower_bound(val.begin(), val.end(), op.y) - val.begin()] += op.p;
    vec.clear();
    rep(i,0,szx-1) rep(j,0,szx-1){
        s[i][j] += (i ? s[i-1][j] : 0) + (j ? s[i][j-1] : 0) - (i&&j ? s[i-1][j-1] : 0);
        if(s[i][j]) insert(val[i], val[j], val[i+1]-1, val[j+1]-1, 1);
    }
    return vec;
}

int main(){
    int T = read();
    while(T--){
        init(), gen();
        m = read(); int type, u, v;
        dfs(1, 0);
        rep(i,1,m){
            type = read(), u = read(), v = read();
            int p = dfn[u][0], q = dfn[v][0];
            if(type == 1){
                Q.push_back({p, q, i, 1}), Q.push_back({p-1, q, i, -1});
                Q.push_back({p, q-1, i, -1}), Q.push_back({p-1, q-1, i, 1});
            } else Q.push_back({p, q, i, 1});
        }

        rep(i,1,n) S[dfn[i][0]]++, S[dfn[i][1]]--;
        rep(i,1,2*n) S[i] += S[i-1];

        int tot = 0;
        rep(i,1,n) color[a[i]].push_back(i);
        rep(i,1,n) for(oper op : work(i)) bucket[op.x].push_back(op), tot++;

        rep(i,1,2*n) if(bucket[i].size() > 1)
            sort(bucket[i].begin(), bucket[i].end(), [&](oper a, oper b){ return a.y < b.y; });
        sort(Q.begin(), Q.end(), [&](query a, query b){ return a.a < b.a; });

        int it = 0;
        for(query q : Q){
            while(it <= q.a){
                int siz = bucket[it].size();
                for(int i = 0; i < siz; ){
                    oper op = bucket[it][i++];
                    while(i < siz && bucket[it][i].x == op.x && bucket[it][i].y == op.y) op.p += bucket[it][i++].p;
                    T0.update(op.y, op.p);
                    T1.update(op.y, S[op.y-1] * op.p);
                    T2.update(op.y, S[op.x-1] * op.p);
                    T3.update(op.y, (ll)S[op.x-1] * S[op.y-1] * op.p);
                }
                it++;
            }
            ans[q.id] += q.k * ((ll)S[q.a]*S[q.b]*T0.get(q.b) - S[q.a]*T1.get(q.b) - S[q.b]*T2.get(q.b) + T3.get(q.b));
        }

        rep(i,1,m) printf("%lld\n", ans[i]);
    }
    return 0;
}