快速沃尔什变换
FWT (Fast Walsh-Hadamard Transform) 快速沃尔什变换
要求 \(C(x)=\sum_{i\otimes j=x}A(i)B(j)\)，\(\otimes\) 是二进制下的一种变换，如 \(\cap,\cup,\oplus\) 或者一些自定义运算。
类似 \(FFT\)，我们对 \(A(x),B(x)\) 做线性变换变为 \(A'(x),B'(x)\)，然后对应值相乘，即 \(C'(x)=A'(x)B'(x)\)，对 \(C'(x)\) 做逆变换后得到 \(C(x)\) 。
设在变换中，\(F'(x)=\sum_{i=0}^n g(x,i)F(i)\)：
第 4 步到第 5 步可以互推，取特定的 \(A(j)=B(k)=1\)，剩下为 \(0\) 即证。
于是若 \(g(x,i)\) 满足:
就可以作为 \(FWT\) 变换的一种方案，当然，由于我们在求值，\(g(x,i)\) 也需要是可以逆变换的。
这里主要考虑按位的二进制变换（诡异如 \(i\otimes j=\text{count}(i)\cdot \text{count}(j)\) 这种通常不太可做），那么其实只要使得 \(0\) 和 \(1\) 处的关系满足上式，然后令最终的对应 \(g(x,i)\) 是每一位的 \(g'(x,i)\) 之乘积即可。同时由于要可逆，变换系数应是非平凡的，于是乎对于常见的 \(\otimes\) 运算就很好构造了：
-
\(\cup\)：
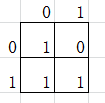即 \(g(x,i)=[i\sub x]\) -
\(\cap\)：
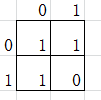即 \(g(x,i)=[i\supset x]\) -
\(\oplus\)：稍微麻烦一些，不过注意到
\[\begin{cases} g(x,0)=g(x,0)^2=g(x,1)^2\\ g(x,1)=g(x,0)g(x,1) \end{cases} \]而且 \(x\) 分别为 \(0,1\) 时两者的系数还要不一样，
于是：
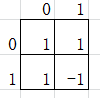\(g(x,i)=(-1)^{|x\cap i|}\)其它的一些对应方案不一定可以，如 \(((1,-1),(-1,1)),\;g(x,i)=(-1)^{|x\oplus i|}\)，这就没法求逆。
现在我们已经会构造合适的线性变换 \(g(x,i)\) 了，考虑对 \(F(x)\) 求出 \(F'(x)\) 。这里可以借鉴 \(FFT\) 的思路，从低位到高位逐步变换，可以发现，实际上就是 \(g(x,i)\) 每次多乘上当前位的 \(g'(x,i)\) 的系数。
设 \(a_0,a_1\) 为当前位是 \(0\) 和 \(1\) 的部分对应的两个序列，那么有：
而逆变换则类似矩阵求逆：
每一位的贡献是独立的，因此逆变换不用倒过来从高位到低位还原，和正变换从低到高也是可以的。
于是每次 \(O(n\log n)\) 求解即可。
三者的 code：
void OR(ll *a, int op){
for(int i = 1; i < 1<<n; i <<= 1)
for(int j = 0; j < 1<<n; j += i<<1)
rep(k,0,i-1) (a[i+j+k] += a[j+k] * op) %= mod;
}
void AND(ll *a, int op){
for(int i = 1; i < 1<<n; i <<= 1)
for(int j = 0; j < 1<<n; j += i<<1)
rep(k,0,i-1) (a[j+k] += a[i+j+k] * op) %= mod;
}
void XOR(ll *a, int op){
for(int i = 1; i < 1<<n; i <<= 1)
for(int j = 0; j < 1<<n; j += i<<1) rep(k,0,i-1){
ll v1 = a[j+k], v2 = a[i+j+k];
a[j+k] = (v1 + v2) % mod, a[i+j+k] = (v1 + mod - v2) % mod;
if(op == -1) (a[j+k] *= inv2) %= mod, (a[i+j+k] *= inv2) %= mod;
}
}
一个应用：
给定序列 \(\{a_n\},\{b_n\}\)，求 \(\displaystyle \sum_{p=1}^n\sum_{k=1}^{+\infty} d_{p,k}\cdot c_{p}^k\)，其中 \(\displaystyle d_{p,k}=\sum_{k=i\oplus j}a_i\cdot b_j\;(1\leq i,j\leq \frac{n}{p})\)，\(\oplus\) 为三进制下按位取 \(\gcd\) 。\(n\leq 2\times 10^5\)
还是按位考虑，\(i,j,\gcd(i,j)\) 是这么个关系：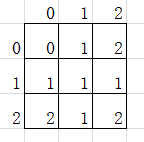
对于 \(i=0,1,2\) 都满足 \(g(x,i)^2=g(x,i)\)，那么取值只能是 \(0\) 或 \(1\) 。可以发现满足条件的 \(g(x,*)\) 有三组：\((1,0,1),(1,1,1),(1,0,0)\)，于是将这三组任意分配给三行即可：
逆变换就是对矩阵 \(g\) 求逆：
求一个 \(d_p\) 是 \(O(len\log len)\) 的，\(\sum len = O(n\ln n)\)，所以时间复杂度是 \(O(n\log^2 n)\) 。
HDOJ 关掉前写的代码，\(g\) 的顺序稍有不同。
#include<iostream>
#include<cstdio>
#include<cstring>
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 660000
#define mod 1000000007
#define ll long long
using namespace std;
inline int read(){
int s = 0, w = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){ if(ch == '-') w = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') s = (s<<3)+(s<<1)+(ch^48), ch = getchar();
return s*w;
}
ll A[N], B[N], C[N], D[N], tA[N], tB[N];
int n, m;
void Trans(ll &x, ll &y, ll &z){
ll a = x, b = y, c = z;
x = a, y = (a+b+c)%mod, z = (a+c)%mod;
}
void iTrans(ll &x, ll &y, ll &z){
ll a = x, b = y, c = z;
x = a, y = (b-c+mod)%mod, z = (c-a+mod)%mod;
}
void FWT(ll *a, int id){
for(int i = 1; i < m; i *= 3)
for(int j = 0; j < m; j += (i*3)) rep(k,0,i-1){
if(id == 0) Trans(a[j+k], a[j+k+i], a[j+k+2*i]);
else iTrans(a[j+k], a[j+k+i], a[j+k+2*i]);
}
}
int main(){
n = read();
rep(i,1,n) tA[i] = A[i] = read();
rep(i,1,n) tB[i] = B[i] = read();
rep(i,1,n) C[i] = read();
ll ans = 0;
rep(p,1,n){
int lim = n/p;
rep(i,1,lim) A[i] = tA[i], B[i] = tB[i];
m = 1;
while(m <= lim) m *= 3;
FWT(A, 0), FWT(B, 0);
rep(i,0,m-1) D[i] = (A[i]*B[i])%mod;
FWT(D, 1);
ll pow = 1;
rep(i,1,m) (pow *= C[p]) %= mod, (ans += pow*D[i]) %= mod;
rep(i,0,m) A[i] = B[i] = D[i] = 0;
}
cout<<ans<<endl;
}
这是官方题解：
每个数列采用的 \(FWT\) 变换矩阵甚至可以不同，算是从一个更高的角度看待快速沃尔什变换了。
