Atcoder AGC034 D - Manhattan Max Matching
题目链接
Atcoder AGC034 D - Manhattan Max Matching
题目大意
在平面上有 \(N\) 处位置放置了一些红球,第 \(i\) 个位置 \((RX_i,RY_i)\) 上放了 \(RC_i\) 个,有 \(N\) 处位置放置了一些蓝球,位置 \((BX_i,BY_i)\) 处放了 \(BC_i\) 个。满足 \(\sum RC_i=\sum BC_i\) 。
要将每个红球蓝球两两配对,使得配对的球之间的曼哈顿距离总和最大,求最大值。
\(N\leq 1000,\;\sum RC_i=\sum BC_i \leq 10000\)
思路
记 \(n=\sum RC_i\) 。
一个球对于距离总和只有 \(4\) 种贡献:\(x+y,x-y,y-x,-x-y\)。于是题目相当于对每个球选择一个合法的贡献方案,然后贡献求和。
一个不合适的角度是从 \(DP\) 入手,(似乎)无法做到 \(O(n^3)\) 以内。
考虑匹配,对红球蓝球建立二分图,每对球之间连上对应可能合法的 \(4\) 种边权,然后答案即二分图最大权匹配,由于最终两者之间的距离必然是 \(4\) 类边权中的最大者,所以正确性可以保证。
球的贡献只有 \(4\) 种,显然可以优化建图,在左右部点之间建 \(4\) 个中间点,每个球按照分别向中间点连对应的权值,当然红球和蓝球的权值是相反的。源点 \(S\) 到红球 与 蓝球到汇点 \(T\) 的边的容量是对应点的 \(RC_i/BC_i\),而权值作为费用,然后跑最大费用最大流即可。
最大流大小是 \(O(n)\) 的,从而时间复杂度 \(O(nN\log N)\) 。
如果以 \(n\) 为规模,每个球都单独建一个节点,可以发现图的性质非常好,边容量全为 \(1\),可以考虑模拟费用流。
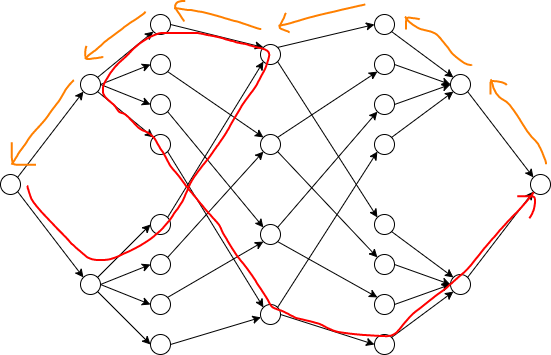
主要是要处理每次退流的情况,在加流的时候,先从 \(S\) 到达一个左部节点,然后从该节点到一个中间节点,接下来有可能会 “往左边绕圈”,即沿着一条退流的边,回到左部的另一个节点上,然后从当前节点到达另一个中间节点(相当于反悔此节点之前的选择,换一个贡献的权值),同时也有可能 “往右边绕圈”,沿着正向边走到一个右部点,然后右部点反悔,沿退流边前往再另一个中间点。最后从一个中间节点到右部点然后到 \(T\) 。
所以加流的过程分为 \(3\) 步:
- 从 \(S\) 经过一个左部点到达一个中间点。
- 中间点之间通过 “左右绕圈” 的方式遍历若干。
- 从一个中间点经过右部点到达 \(T\) 。
第 \(2\) 步是一个类似于最长路的东西,其中两个中间点之间的边权是,通过绕一次圈到达另一个点过程中经过的边费用之和,这里要在 “左右绕圈” 两个方向里取较大值。
而 \(1\) 和 \(3\) 两步只需对每个中间点分别维护到 \(S\) 和 \(T\) 的最大费用的点即可。
具体实现的话,记 \(w[i][d]\) 表示节点 \(i\) 到中间点 \(d\) 连的费用,那么最长路中 \(u\rightarrow v\) 的边权即 \(\displaystyle \max(\max_{i\in left}\{-w[i][u]+w[i][v]\},\max_{j\in right}\{w[j][u]-w[j][v]\})\) ,其中 \(i\) 和 \(j\) 之前分别是选择了 \(u,v\) 这两种权值的。然后 \(Floyd\) 跑最长路,最后取 \(\arg \max\{w_S(u)+dis_{i,j}+w_T(v)\}\) 作为路径端点,记录最长路上的权值类型,以及 \(w_S(u)\) 和 \(w_T(v)\) 对应的左右节点,然后更新涉及到的 \(i,j\) 的归属即可。
两类边权可以用堆来维护,开 \(16\) 个 priority_queue 即可。\(w_S(u),w_T(u)\) 的候选节点只会减少不会增加,于是可以将节点先排好序,然后拿指针单调维护。
于是时间复杂度为 \(O(n\log n)\),有一个 \(C=21\) 左右的常数,\(n=2.5e5\) 的范围要 \(360\) ms 左右,原题 \(22\) ms,目前在最优解中 rank 4 。
Code
#include<bits/stdc++.h>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 250025
#define PLI pair<ll, int>
#define fr first
#define sc second
#define ll long long
#define Inf 0x3f3f3f3f3f3f3f3f
using namespace std;
int n, m, rx[N], ry[N], bx[N], by[N];
ll w[2*N][4];
PLI lq[4][N], rq[4][N]; int itl[4], itr[4];
priority_queue<PLI> ql[4][4], qr[4][4];
ll dis[4][4];
bool type[4][4], vis[2*N], rem[4][2*N];
vector<int> path[4][4];
bool Max(ll &a, ll b){ return a < b ? a = b, 1 : 0; }
bool check(int u, priority_queue<PLI>& q){
while(!q.empty() && !rem[u][q.top().sc]) q.pop();
return !q.empty();
}
void insert(int d, int x){
rem[d][x] = vis[x] = true;
rep(b,0,3) if(b != d)
(x <= n ? ql[d][b] : qr[b][d]).push({w[x][b] - w[x][d], x});
}
ll flow(){
rep(d,0,3){
dis[d][d] = 0;
rep(b,0,3) if(b != d){
dis[d][b] = -Inf;
if(check(d, ql[d][b]) && Max(dis[d][b], ql[d][b].top().fr)) type[d][b] = true;
if(check(b, qr[d][b]) && Max(dis[d][b], qr[d][b].top().fr)) type[d][b] = false;
path[d][b] = {d, b};
}
}
rep(k,0,3) rep(i,0,3) rep(j,0,3)
if(Max(dis[i][j], dis[i][k] + dis[k][j])){
path[i][j] = path[i][k], path[i][j].pop_back();
for(int l : path[k][j]) path[i][j].push_back(l);
}
ll mx = -Inf; int u = 0, v = 0;
rep(i,0,3) rep(j,0,3) if(itl[i] && itr[j])
if(Max(mx, dis[i][j] + lq[i][itl[i]].fr + rq[j][itr[j]].fr)) u = i, v = j;
if(u != v) rep(i,0,(int)path[u][v].size()-2){
int a = path[u][v][i], b = path[u][v][i+1];
int x = (type[a][b] ? ql : qr)[a][b].top().sc;
if(!type[a][b]) swap(a, b);
rem[a][x] = false, insert(b, x);
}
insert(u, lq[u][itl[u]].sc);
insert(v, rq[v][itr[v]].sc);
rep(d,0,3){
while(itl[d] && vis[lq[d][itl[d]].sc]) itl[d]--;
while(itr[d] && vis[rq[d][itr[d]].sc]) itr[d]--;
}
return mx;
}
int main(){
ios::sync_with_stdio(false);
cin>>m;
int num;
rep(i,1,m){
n++, cin>>rx[n]>>ry[n]>>num;
while(--num) n++, rx[n] = rx[n-1], ry[n] = ry[n-1];
}
n = 0;
rep(i,1,m){
n++, cin>>bx[n]>>by[n]>>num;
while(--num) n++, bx[n] = bx[n-1], by[n] = by[n-1];
}
rep(i,1,n) rep(p,0,1) rep(q,0,1)
w[i][p*2+q] = rx[i] * (p?-1:1) + ry[i] * (q?-1:1);
rep(i,1,n) rep(p,0,1) rep(q,0,1)
w[i+n][3-p*2-q] = bx[i] * (p?-1:1) + by[i] * (q?-1:1);
rep(d,0,3){
rep(i,1,n) lq[d][i] = {w[i][d], i}, rq[d][i] = {w[i+n][d], n+i};
sort(lq[d]+1, lq[d]+n+1), sort(rq[d]+1, rq[d]+n+1);
itl[d] = itr[d] = n;
}
ll ans = 0;
rep(_,1,n) ans += flow();
cout<< ans <<endl;
return 0;
}



