HDOJ 6991 Increasing Subsequence

题目链接

HDOJ 6991 Increasing Subsequence (Minieye 杯联赛第四场 T7)

题目大意

定义极大上升子序列为「不为任意一个上升子序列的真子集」的上升子序列，给定一个长度为 \(n\) 的排列，求其极大上升子序列个数，答案对 \(998244353\) 取模。

\(1\leq n\leq 10^5\)

思路

观察 极大上升子序列 的定义，可以发现其等价于要求序列的相邻两项 \(i,j\)​​，满足 \(\forall i<k<j,\;a_k<a_i\bigvee a_k>a_j\)​​​ ，于是可以考虑 \(dp\)，记 \(dp_i\) 为以 \(a_i\) 结尾的极大上升子序列的数量，则 \(dp_j\) 向 \(dp_i\) 转移的条件如上，相当于在去除大于 \(a_i\) 的元素之后，\(a_j\) 是从 \(i\) 往前的后缀最大值。而初值 \(dp_i=[a_i=min_{1\leq j\leq i}\{a_j\}]\)，当 \(a_i\) 是前缀最小值时才能作为一个极大上升子序列的开头，答案为所有后缀最大值位置的 \(dp\) 值之和。

朴素地做是 \(O(n^2)\)​ 的，想了半天没有找到用数据结构优化转移的做法，难点在对于每个 \(a_i\)​ 转移位置构成的单调序列，它们之间没有什么有用的共同点，这个时候可以尝试换个角度，考虑使用分治。这样问题就转化成了对于区间 \([l,r]\)​，如何将左半区间的 \(dp\)​​​ 值转移到右半边上。

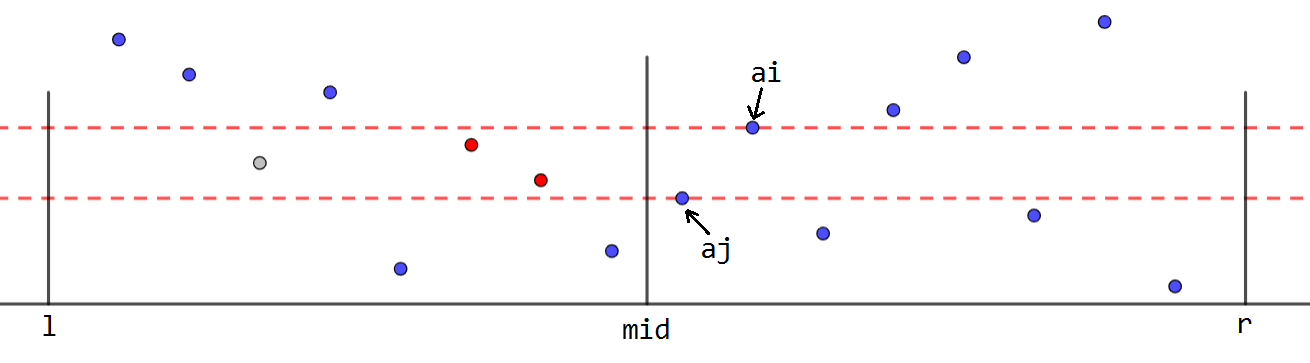
观察上图，对于当前在计算的点 \(a_i\)，我们需要找到在 \(i\) 前面的右半区间中，最大的比 \(a_i\) 小的元素 \(a_j\)，能够向 \(dp_i\) 转移的 \(k\) 都需要满足 \(a_j<a_k<a_i\)，即两虚线所夹的区域，同时在左半区间内，这些可以转移的点还构成从右往左的单增序列，不在序列内的则无法转移。

观察到这些性质，肯定是要用单调数据结构来维护这些转移点，注意到右半区间「最大的比 \(a_i\) 小的点」以及左半区间随着红线上升，转移点时刻呈单减序列，可以想到用两个以 \(a_i\) 作为顺序，\(i\)​ 作为关键字的单调栈 \(left,right\) 来维护这些信息。具体来说，我们按照 \(a_i\) 从小到大逐个把点加入左/右半区间的单调栈中，右半区间加入一个 \(a_i\)​ 时，\(right\) 的顶部剩下来的即为 \(j\)，然后在 \(left\) 中找到第一个 \(>a_j\) 的位置 \(pos\)，则 \(left\) 栈中 \([pos,end]\) 上的所有位置都可转移到 \(dp_i\)​，我们同时随着 \(left\) 维护一个前缀和即可 \(O(1)\) 进行转移。

二分 \(pos\) 是 \(O(\log n)\) 的，所以时间复杂度 \(O(n\log^2n)\) 。

Code

#include<iostream>
#include<algorithm>
#include<vector>
#include<numeric>
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 101000
#define ll long long
#define mod 998244353
#define Inf 0x3f3f3f3f
using namespace std;

int a[N], n;
ll sum[N], dp[N];

bool cmp(int i, int j){ return a[i] < a[j]; }

void solve(int l, int r){
    if(l == r) return;
    int mid = (l+r)>>1;
    solve(l, mid);

    vector<int> pos(r-l+1);
    vector<int> left, right;
    iota(pos.begin(), pos.end(), l);
    sort(pos.begin(), pos.end(), cmp);
    for(int i : pos){
        if(i <= mid){
            while(!left.empty() && left.back() < i) left.pop_back();
            left.push_back(i);
            int siz = left.size();
            sum[siz] = sum[siz-1]+dp[i]; 
        } else{
            while(!right.empty() && right.back() > i) right.pop_back();
            if(left.empty()) continue;
            int lb = right.empty() ? 0 : lower_bound(left.begin(), left.end(), right.back(), cmp) - left.begin();
            (dp[i] += sum[left.size()] - sum[lb] + mod) %= mod;
            right.push_back(i);
        }
    }
    solve(mid+1, r);
}

int main(){
    ios::sync_with_stdio(false);
    int T; cin>>T;
    while(T--){
        cin>>n;
        rep(i,1,n) cin>>a[i];

        int mn = Inf;
        rep(i,1,n){
            if(mn > a[i]) mn = a[i], dp[i] = 1;
            else dp[i] = 0;
        }
        solve(1, n);
        int mx = 0;
        ll ans = 0;
        per(i,n,1) if(mx < a[i]) mx = a[i], (ans += dp[i]) %= mod;

        cout<< ans <<endl;
    }
    return 0;
}