后缀自动机学习笔记
定义和一些记号
定义
自动机由 \(5\) 个模块组成:
- \(\Sigma\) :字符集
- \(state\) : 状态集合
- \(init\) : 初始状态(只有一个)
- \(end\) : 终止状态集合
- \(Trans(s,c)\) : 转移函数,状态 \(s\) 在接受字符 \(c\) 之后,返回下一个状态
一个字符串 \(S\) 的后缀自动机(\(SAM\),Suffix Automaton)是其最小的确定有限状态自动机(\(DFA\) ,Deterministic Finite Automaton),仅接受\(S\) 的所有后缀,即只在输入后缀后,自动机会达到终止状态。
记号
\(null\) : 不存在状态,若 \(s\) 无法接受字符 \(c\),则 \(Trans(s,c)=null\)。同时定义 \(Trans(null,*)=null\)
\(ST(str)\) : \(Trans(init,str)\),即从初始状态开始输入 \(str\) 之后得到的状态。
\(str[l,r]\) : 字符串 \(str\) 中下标 \(\in[l,r]\) 的子串
\(Fac\) : 子串集合
\(Right(s)\) : 状态 \(s\) 在字符串中出现的所有位置的集合,即 \(Right(s)=\{r\;|ST(str[l,r])=s\}\)
\(Reg(A)\) : 自动机 \(A\) 能够识别的字符串的集合
\(Reg(s)\) : 从状态 \(s\) 开始能够识别的字符串的集合,即 \(Reg(s)=\{str\;|Trans(s,str)\in end\}\)
前置性质
如果用朴素的想法去实现 \(SAM\) 的功能,其实只需将字符串 \(str\) 的所有后缀拿出来建一棵 \(Trie\) 即可,不过这样的状态数是 \(O(n^2)\) 级别的,我们需要将自动机的状态数简化。观察两个串 \(a\) 和 \(b\),如果 \(Reg(a)=Reg(b)\),可以发现两者在自动机上被处理的方式完全相同,从而我们将这些串合并起来,储存在同一个状态 \(s\) 中。
在进一步讨论之前,我们先分析一些性质。
- 达到状态 \(s\) 的字符串其长度构成一段区间,我们设其为 \([Min(s),Max(s)]\)
这些字符串达到状态 \(s\),说明它们在原串中的出现次数等于 \(|Right(s)|\),而这些串之间为后缀关系,一个串在原串中的出现次数随着其长度增加而减小,且其母串的出现位置为自己的子集,所以出现次数为 \(|Right(s)|\) 这一值的串长构成一段区间。
- 对于两个状态 \(a\) 和 \(b\),要么 \(Right(a)\bigcap Right(b)=\emptyset\),要么 \(Right(a)\subset Right(b)\) 或者 \(Right(a)\supset Right(b)\) 。
考虑 \(Right(a)\bigcap Right(b)\neq \emptyset\) 的情况,设 \(r\in Right(a)\bigcap Right(b)\),对于这个位置,两者的 \(len\) 区间不能有交,否则就存在一个字符串同时能够到达两个状态了,由于 \(SAM\) 是 \(DFA\),这种情况不被允许。那么我们设 \(Max(a) < Min(b)\),则 \(a\) 中所包含的字符串均为 \(b\) 中字符串的后缀,\(b\) 中字符串是由 \(a\) 中延伸出来的,从而有 \(Right(a)\supset Right(b)\) 。
有了性质 \(2\),我们可以用树的方式将状态之间联系起来,引入父亲的概念:
\(par(s)\) : 最小的满足 \(Right(s)\) 为其 \(Right\) 子集的状态
我们将建出的这棵树称为 \(Parent\;\;Tree\),再分析 \(Parent\;\;Tree\) 的性质:
- 每一个非叶子节点都有至少 \(2\) 个儿子。
由于父亲儿子之间的 \(Right\) 是真子集关系,而每一个位置都要被一个状态认领,性质成立。
- \(Parent\;\;Tree\) 至多有 \(n\) 个叶子节点,总共至多有 \(2n-1\) 个节点。
叶子节点就是字符串匹配到最后的情况,仅剩下一个可能位置,显然至多有 \(n\) 种这样的情况,比如 \(str=aaaaa\) 的时候,叶子节点就只有 \(1\) 个。由于至少是二叉树,显然至多有 \(2n+1\) 个节点。
由于 \(Parent\;\;Tree\) 是由所有状态构成的,性质 \(4\) 说明了 \(SAM\) 的状态数至多有 \(2n-1\) 种。
我们再来证明 \(SAM\) 状态之间的转移数量是 \(O(n)\) 的。
- \(SAM\) 的状态转移数量 \(\leq 3n-4\)
我们取出 \(SAM\) 状态转移关系构成的图的最长路径生成树。
对于树边,根据前面的结论其数量 \(\leq 2n-2\)
对于非树边,考虑一条非树边 \(a\rightarrow b\),我们先从 \(init\) 沿着树边走到 \(a\),然后经过 \(a\rightarrow b\) 走到 \(b\),令这条非树边对应所有 \(b\) 继续沿着非树边最终可以到达的后缀,显然至少有一个。对于每一个后缀,如果它匹配的过程中经过了非树边,则让其对应经过的第一条非树边,从而每个后缀最多对应一条非树边。所以非树边的数量 \(\leq\) 后缀的数量,由于这里是最长路径生成树,\(str\) 本身不经过非树边,所以非树边数量 \(\leq n-1\)
但是两种情况无法同时取等,可以说明总共的转移数量 \(\leq 3n-4\)
在愉快地构建 \(SAM\) 之前,再观察一些性质,记 \(t=Trans(s,c), \;fa=par(s)\) 。
- \(Right(t)=\{r+1\;|r\in Right(s),s[r+1]=c\}\),\(SAM\) 是一个 \(DAG\) 。
前者根据定义显然,由于 \(r\) 一直在增加,不会出现环的情况,所以 \(SAM\) 是一个 \(DAG\) 。
- \(Max(t)>Max(s)\)
\(Max(s)\) 对应的那个字符串多增加了 \(c\) 字符,显然要变大了。
- \(Trans(s,c)\neq null \Rightarrow Trans(fa,c)\neq null\)
\(Right(fa)\supset Right(s)\),显然
- \(Max(fa)=Min(s)-1\)
根据合法的 \(len\) 的连续性可证。
- \(Right(Trans(s,c))\subseteq Right(Trans(fa,c))\)
\(Parent\;\;Tree\) 的包含关系所保证。
- \(ST(str)\neq null\iff str\in Fac\)
这些性质不会在构造中全部用到,但是在实际应用 \(SAM\) 的时候很重要。
构建 \(SAM\)
假设当前已经有了 \(T\) 的 \(SAM\),考虑构建 \(T+x\) 的 \(SAM\),设 \(L=|T|\)。
-
找到状态 \(u\) 满足 \(Right(u)=\{L\}\),\(u\) 是 \(Parent\;\;Tree\) 的一个叶子节点。
-
构造状态 \(u'\),\(Right(u')=\{L+1\}\),\(Max(u')=L+1\) 。
-
现在考虑从 \(u\) 到 \(init\) 的这一段链,将节点依次记为 \(v_1,v_2,...,v_k\)(\(v_k=init\)),找到 \(Trans(v,x)=null\) 的所有状态,它们应为 \(\{v\}\) 的一段前缀,令 \(Trans(v,x)=u'\) 。
-
找到第一个 \(Trans(v,x)\neq null\) 的状态 \(v_p\) :
若 \(v_p\) 不存在,则令 \(par(u')=init\) (因为链上除了 \(init\) 没有节点的 \(Right\) 能包含 \(u'\))
若 \(v_p\) 存在,设 \(q=Trans(p,x)\),有 \(Max(q)\geq Max(v_p)+1\),分两种情况:
(图中的横线为 \([r_i-Max(s)+1, r_i]\))
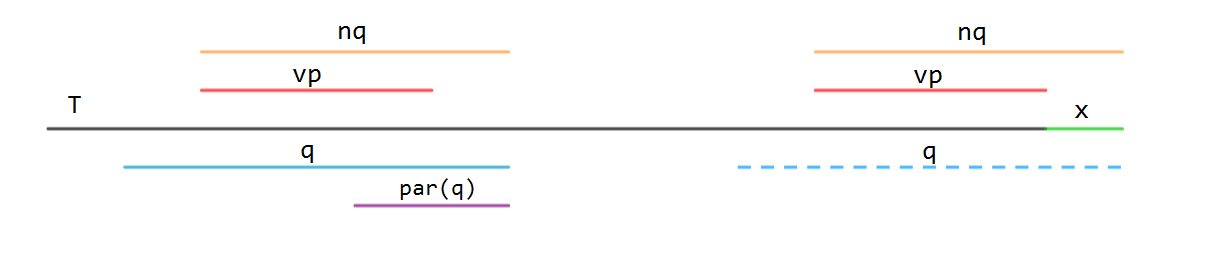
-
\(Max(q)=Max(v_p)+1\)
此时 \(v_p\) 中的所有字符串都可以直接拓展到 \(L+1\),因为红线和蓝线左端对齐了,那么红线区域中的字符串可以,蓝色的也可以。令 \(par(u')=q\) 即可。
-
\(Max(q)>Max(v_p)+1\)
这个时候 \(q\) 中的串不止 \(vp\) 中的,有一些更长的可能匹配不了 \(x\),如右边蓝色虚线部分,如果强行转过去,\(Max(q)\) 就反而变小了,这可能会导致一系列问题。为了解决这种情况,我们新建一个结点 \(nq\),将 \(q\) 里 \(len\leq Max(v_p)+1\) 的字符串给 \(nq\),\(L+1\) 那一块转移也交给 \(nq\) 处理。
由于 \(L+1\) 以外的位置还没法转移,所以 \(nq\) 的转移情况是和 \(q\) 完全一样的,\(Trans(nq,*)=Trans(q,*)\)。而 \(par(nq)\) 即为先前 \(SAM\) 中的 \(par(q)\),由图,可以知道有这样的变化:
\[par(q)\leftarrow nq,\; par(u')\leftarrow nq \]然后我们找到所有满足 \(Trans(v,x)=q\) 的结点(是 \(v_p\) 到 \(v_e\) 的一段区间),现在 \(q\) 已经满足不了 \(L+1\) 的转移需求了,但是 \(nq\) 可以,所以将 \(Trans(v,x)\) 改为 \(nq\) 。
然后就没了。初始是 \(SAM\) 是单独一个结点 \(init\),每次增量构造即可。
时间复杂度
- 对于原先 \(Trans(v,x)=null\),后来改为 \(u'\) 的结点,这个操作增加了一个转移,先前证转移数是 \(O(n)\) 的,从而该操作是 \(O(n)\) 的。
- 增加新结点 \(nq\) 的操作是和总结点数挂钩的,总节点数 \(O(n)\),从而此操作 \(O(n)\) 。
- 对于将 \(Trans(v,x)\) 改为 \(nq\) 这个操作,时间复杂度证明:
记 \(lst\) 为上一次的 \(u\),每一次构造后它变为 \(u'\),观察 \(Min(par(lst))\) 的变化情况:
\[Min(u)=Min(v_1)>Min(v_2)>...>Min(v_e)\geq Min(q)-1\geq Min(nq)-1 \]倒数第二个大于等于是因为 \(q\) 向右拓展了一个 \(x\),所以会增加,最后一个大于等于即继承关系。可以发现在链上往上走的过程中,\(Min\) 一直减小,到了 \(q\) 处才可能会加 \(1\),而下一次往上跳的时候经过 \(nq\) 就直接到 \(v_{e-1}\) 处了,\(Min\) 会减少至少 \(1\),而 \(Min\) 最大为 \(|S|\),从而总时间复杂度为 \(O(n)\) 的。
综上,\(SAM\) 的构造时间复杂度为 \(O(n)\) 。
代码实现
话说着很多,但是代码还挺短的,这里的 \(len\) 即 \(Max(s)\),\(link\) 即 \(par(s)\) 。
struct Suffix_Automaton{
struct state{
int len, link;
int next[26];
} t[N<<1];
int cnt, lst;
void init(){
t[1].len = 0, t[1].link = 0;
mem(t[1].next, 0);
cnt = 1, lst = 1;
}
void extend(int c){
int cur = ++cnt;
t[cur].len = t[lst].len+1;
mem(t[cur].next, 0);
int u = lst;
while(u && !t[u].next[c])
t[u].next[c] = cur, u = t[u].link;
if(u == 0) t[cur].link = 1;
else{
int q = t[u].next[c];
if(t[q].len == t[u].len+1) t[cur].link = q;
else{
int nq = ++cnt;
t[nq].len = t[u].len+1;
memcpy(t[nq].next, t[q].next, sizeof(t[nq].next));
t[nq].link = t[q].link;
t[q].link = t[cur].link = nq;
while(u && t[u].next[c] == q)
t[u].next[c] = nq, u = t[u].link;
}
}
lst = cur;
}
} SAM;
应用
\(SAM\) 其特殊之处在于它维护的是后缀信息,但是读取串却是从前往后读的,所以它能够解决众多子串类型的问题,其中最典型的一个,即 \(ST(T)\neq null \iff T\in Fac\) 。
CF123D String
给定一个串 \(S\),记 \(f(t)\) 为串 \(t\) 在 \(S\) 的出现次数,求 \(\sum_{t\subseteq S}\frac{f(t)(f(t)-1)}{2}\) ,\(|S|\leq 10^5\) 。
我们只需要维护每个子串的出现次数即可,即该串对应的状态 \(s\) 的 \(|Right(s)|\),注意到 \(Right(s)\) 即为其子树中所有节点 \(Right\) 的并集,那么只需在建 \(SAM\) 的时候,在第一个 \(Right\) 中包含 \(L+1\) 的节点,即新添的 \(u'\) 上记录一下即可。具体来说,维护状态的一个属性 \(siz=|Right(s)|\),每次在 \(u'\) 的地方 \(siz\) 设为 \(1\),表示 \(L+1\) 的出现,然后自底向上贡献到父亲的 \(siz\) 中。一个节点中的字符串数量即为 \(Max(s)-Min(s)+1=Max(s)-Max(par(s))\),将它们的值加入答案中即可。
时间复杂度 \(O(n)\)
Code
#include<iostream>
#include<cstring>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 101000
#define ll long long
#define t(x) SAM.t[x]
using namespace std;
struct Suffix_Automaton{
struct state{
int len, link, siz;
int next[26];
} t[N<<1];
int cnt, lst;
void init(){ cnt = lst = 1; }
void extend(int c){
int cur = ++cnt;
t[cur].len = t[lst].len+1, t[cur].siz = 1;
int u = lst;
while(u && !t[u].next[c])
t[u].next[c] = cur, u = t[u].link;
if(u == 0) t[cur].link = 1;
else{
int q = t[u].next[c];
if(t[q].len == t[u].len+1) t[cur].link = q;
else{
int nq = ++cnt;
t[nq].len = t[u].len+1;
memcpy(t[nq].next, t[q].next, sizeof(t[nq].next));
t[nq].link = t[q].link;
t[q].link = t[cur].link = nq;
while(u && t[u].next[c] == q)
t[u].next[c] = nq, u = t[u].link;
}
}
lst = cur;
}
} SAM;
int head[2*N], to[2*N], nxt[2*N];
int cnt;
string s;
ll ans;
void init(){ mem(head, -1), cnt = -1; }
void add_e(int a, int b){
nxt[++cnt] = head[a], head[a] = cnt, to[cnt] = b;
}
void dfs(int x){
for(int i = head[x]; ~i; i = nxt[i])
dfs(to[i]), t(x).siz += t(to[i]).siz;
ans += (ll)(t(x).len-t(t(x).link).len) * t(x).siz * (t(x).siz+1) / 2;
}
int main(){
ios::sync_with_stdio(false);
cin>>s;
SAM.init();
for(char c : s) SAM.extend(c-'a');
init();
rep(i,2,SAM.cnt) add_e(t(i).link, i);
dfs(1);
cout<<ans<<endl;
return 0;
}
CF235C Cyclical Quest
给定一个主串 \(S\) 和 \(n\) 个串 \(x\),求每个串 \(x\) 的循环同构串在 \(S\) 中的出现次数。
\(|S|\leq 10^6,\;n\leq 10^5,\;\sum|x|\leq 10^6\)
先通过和上面相同的方式将每个状态对应的字符串数量求出来,要求循环同构串的出现次数,考虑将 \(x_i\) 重复两遍作为一个串,在 \(SAM\) 上找所有匹配长度 \(\geq |x_i|\) 的位置数量。
在匹配的过程中,如果当前 \(trans(st,c)\neq null\),则直接走,匹配长度 \(L++\) ,否则一直跳 \(par(st)\) 直到存在转移,如果最终不存在,则 \(st\) 回到 \(init\),\(L=0\),否则 \(L=Max(st)+1\) (这肯定是变小了),\(st=Trans(st,c)\) 。由于 \(|x_i|\) 可能还有循环节,我们直接匹配的时候还要注意去重,若 \(L\geq |x_i|\),则一直跳 \(par(st)\) 直到 \(Max(par(st))<L\),此时的 \(st\) 即为该循环节真正匹配上的状态,\(ans\leftarrow siz_{st}\),在这个节点上记录此次匹配,防止一个状态被重复匹配。
时间复杂度 \(O(n+\sum|x|)\)
Code
Automaton 中的内容和上一份代码完全一样,就不贴了。
#include<iostream>
#include<cstring>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 1001000
#define t(x) SAM.t[x]
using namespace std;
struct Suffix_Automaton{ ... } SAM;
int head[N<<1], to[N<<1], nxt[N<<1];
int cnt;
string s, x;
void init(){ mem(head, -1), cnt = -1; }
void add_e(int a, int b){
nxt[++cnt] = head[a], head[a] = cnt, to[cnt] = b;
}
void dfs(int x){
for(int i = head[x]; ~i; i = nxt[i])
dfs(to[i]), t(x).siz += t(to[i]).siz;
}
int main(){
ios::sync_with_stdio(false);
cin>>s;
SAM.init();
for(char c : s) SAM.extend(c-'a');
init();
rep(i,2,SAM.cnt) add_e(t(i).link, i);
dfs(1);
int T; cin>>T;
rep(o,1,T){
cin>>x;
int m = x.size();
x += x;
int st = 1, l = 0, ans = 0;
rep(i,0,2*m-2){
int c = x[i]-'a';
if(t(st).next[c]) l++, st = t(st).next[c];
else{
while(st && t(st).next[c] == 0) st = t(st).link;
if(st == 0) st = 1, l = 0;
else l = t(st).len+1, st = t(st).next[c];
}
if(i >= m-1 && l >= m){
while(t(t(st).link).len >= m) st = t(st).link;
if(t(st).vis < o) ans += t(st).siz, t(st).vis = o;
l = m;
}
}
cout<<ans<<endl;
}
return 0;
}
UOJ#395. 【NOI2018】你的名字
待更。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号