洛谷 P6918 [ICPC2016 WF]Branch Assignment
题目链接: 洛谷P6918 CodeforcesGym101242B
题目大意
有一张 \(n\) 个点,\(r\) 条带权边的强连通有向图,对于 \(i,j\in [1,b]\) ,\(w(i,j)=dis(i,b+1)+dis(b+1,j)\) ,现在将序号 \(1\) 到 \(b\) 的点划分为 \(s\) 个点集 \(S_1,S_2,...,S_s\),求 \(\sum_{k=1}^s\sum_{i,j\in S_k}w(i,j)\) 的最小值。
\(2\leq n\leq 5 000\) ,\(1\leq s\leq b\leq n-1\) ,边权 \(\in [0,10 000]\)
思路
对于一个集合 \(S\) ,
设 \(a_i=dis(i,b+1)+dis(b+1,i)\) ,则 \(\sum_{i,j\in S}w(i,j)\) 即为 \((|S|-1)\sum_{i\in S}a_i\),设节点 \(i\) 所在的集合大小为 \(h_i\) ,那么有 \(ans=min\{\sum_{i=1}^bh_ia_i\}\) ,根据排序不等式,\(a_i\) 单调递增 \(h_i\) 单调递减时答案最优,由此先将 \(a_i\) 递增排序,取 \(A_i\) 为前缀和,得到一个 \(O(b^2s)\) 的 \(dp\) :
显然 \(w(j,i)=(i-j)(A_i-A_j)\) 满足四边形不等式(这里的 \(w\) 不是原题面中的那个),结合下图,\(A_i\) 和 \(i\) 分别为横纵坐标,\(a\leq b\leq c\leq d\) 时 \(w(a,d)+w(b,c)>w(a,b)+w(c,d)\) :
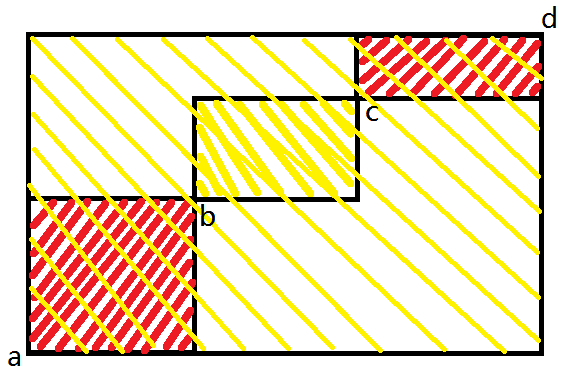
从而最优决策点 \(\xi_{c,i}\) 关于 \(i\) 单增,可将 \(dp\) 优化到 \(O(bslogb)\) ,经过观察,还会注意到 \(\xi_{c,i}\) 同样是对 \(c\) 单增的,
证明:
设 \(x=\xi_{c,i}\),\(y=\xi_{c+1,i}\) ,根据最优决策性应有:
\[dp_{c-1,x}+w(x,i)\leq dp_{c-1,y}+w(y,i)\\ dp_{c,y}+w(y,i)\leq dp_{c,x}+w(x,i) \]移项可得:
\[dp_{c-1,x}-dp_{c-1,y}\leq w(y,i)-w(y,x)\leq dp_{c,x}-dp_{c,y}\\ dp_{c-1,x}+dp_{c,y}\leq dp_{c,x}+dp_{c-1,y} \]由于 \(dp_{c,i}\) 满足四边形不等式,所以 \(x\leq y\) ,从而 \(\xi_{c,i}\) 关于 \(c\) 单增。
所以 \(\xi_{c-1,i}\leq \xi_{c,i}\leq \xi_{c,i+1}\),内层逆序枚举转移即可,时间复杂度:
(中间一步可以画个矩阵自行理解)
这个做法已经可以轻松通过本题了,但是可以发现有一个性质没有用到,即 \(i-\xi_{c,i}\) 应随 \(i\) 增加而减小(后面划分的块要越来越小),利用这个性质,\(dp\) 可以进一步优化到 \(O(nlog^2n)\) ,具体做法在这里。
Code:
\(O(b(b+s))\) 代码
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
#include<fstream>
#define mem(a,b) memset(a,b,sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,b,a) for(int i=(b);i>=(a);i--)
#define N 5050
#define M 50500
#define ll long long
#define PLL pair<ll,ll>
#define mk make_pair
#define fr first
#define sc second
using namespace std;
int head[N],to[M],nxt[M],len[M];
int _head[N],_to[M],_nxt[M];
ll cnt,dis[N],_dis[N];
bool vis[N];
priority_queue<PLL,vector<PLL>,greater<PLL> > q;
int n,b,s,r;
ll a[N],A[N],best[N][N],dp[N][N];
void init(){mem(head,-1),mem(_head,-1),cnt=-1;}
void add_e(int a,int b,int *H,int *NX,int *T){
NX[++cnt]=H[a],H[a]=cnt,T[cnt]=b;
}
bool Min(ll &a,ll b){return a>b?a=b,1:0;}
void dijkstra(ll *d,int *H,int *NX,int *T){
mem(vis,false);
memset(d,0x3f,(n+1)*sizeof(ll));
d[b+1]=0;
q.push(mk(0,b+1));
while(!q.empty()){
int cur=q.top().sc; q.pop();
if(vis[cur])continue;
vis[cur]=true;
for(int i=H[cur];~i;i=NX[i]){
if(Min(d[T[i]],d[cur]+len[i]))
q.push(mk(d[T[i]],T[i]));
}
}
}
int main(){
//freopen("data.in","r",stdin);
//freopen("mine.out","w",stdout);
ios::sync_with_stdio(false);
cin>>n>>b>>s>>r;
init();
int u,v,l;
rep(i,1,r){
cin>>u>>v>>l;
add_e(u,v,head,nxt,to);
cnt--,add_e(v,u,_head,_nxt,_to);
len[cnt]=l;
}
dijkstra(dis,head,nxt,to);
dijkstra(_dis,_head,_nxt,_to);
rep(i,1,b)a[i]=dis[i]+_dis[i];
sort(a+1,a+b+1);
rep(i,1,b)A[i]=A[i-1]+a[i];
mem(dp,0x3f);
dp[0][0]=0;
rep(c,1,s){
best[c][b+1]=b;
per(i,b,0)rep(k,best[c-1][i],min(best[c][i+1],(ll)i))
if(Min(dp[c][i],dp[c-1][k]+(ll)(i-k)*(A[i]-A[k])))best[c][i]=k;
}
cout<<dp[s][b]-A[b]<<endl;
return 0;
}
坑1:数组传指针 ll *d 对其 memeset 的时候不能直接 sizeof(d);,这样的返回值是错的。
坑2:不能对指针指向的数据进行强制类型转换,会CE
\(O(nlog^2n)\) 的做法咕了,有空再补吧。
update on 2021.4.28
补上来了,洛谷最优解,做法是决策单调性+ \(wqs\) 二分,有个注意点,二分的上界比较玄学,设为 \(2nr^2\times10000\) 在第四个点挂了,设成 \(Inf\) 才能过。(这一段时间改进了一下码风)
//This is a solution of O(nlog^2n)
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
#include<fstream>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for (int i = (a); i <= (b); i++)
#define per(i,b,a) for (int i = (b); i >= (a); i--)
#define N 5050
#define M 50500
#define ll long long
#define PLL pair<ll, ll>
#define mk make_pair
#define fr first
#define sc second
#define Inf 0x3f3f3f3f3f3f3f3f
using namespace std;
int head[N], to[M], nxt[M], len[M];
int _head[N], _to[M], _nxt[M];
ll cnt, dis[N], _dis[N];
bool vis[N];
priority_queue<PLL, vector<PLL>, greater<PLL> > q;
int n, b, s, r;
ll a[N], A[N], best[N][N];
PLL dp[N];
struct choice{
int l, r, i;
}c[N];
void init(){ mem(head, -1), mem(_head, -1), cnt = -1;}
void add_e(int a, int b, int *H, int *NX, int *T){
NX[++cnt] = H[a], H[a] = cnt, T[cnt] = b;
}
bool Min(ll &a, ll b){ return a > b ? a = b, 1 : 0; }
void dijkstra(ll *d, int *H, int *NX, int *T){
mem(vis, false);
memset(d, 0x3f, (n+1)*sizeof(ll));
d[b+1] = 0;
q.push(mk(0, b+1));
while (!q.empty()){
int cur = q.top().sc;
q.pop();
if (vis[cur]) continue;
vis[cur] = true;
for(int i = H[cur]; ~i; i = NX[i]){
if (Min(d[T[i]], d[cur] + len[i]))
q.push(mk(d[T[i]], T[i]));
}
}
}
bool better(int i, int j, int k){
return dp[i].fr+(k-i)*(A[k]-A[i]) < dp[j].fr+(k-j)*(A[k]-A[j]);
}
int binary_search(int l, int r, int i, int j){
int mid;
while(l < r){
mid = (l+r)>>1;
if(better(i, j, mid)) r = mid;
else l = mid+1;
}
return l;
}
int cal(ll Cost){
int l = 0, r = 0;
dp[0] = {0, 0};
c[0] = {1, b, 0};
rep(i,1,b){
while(l <= r && c[l].r < i) l++;
c[l].l = i;
dp[i].fr = dp[c[l].i].fr + (i-c[l].i)*(A[i]-A[c[l].i]) + Cost;
dp[i].sc = dp[c[l].i].sc+1;
int pos = b+1;
while(l <= r && better(i, c[r].i, c[r].l)) pos = c[r--].l;
if(l <= r && better(i, c[r].i, c[r].r)) pos = binary_search(c[r].l, c[r].r, i, c[r].i);
if(l <= r) c[r].r = pos-1;
if(pos <= b) c[++r] = {pos, b, i};
}
return dp[b].sc;
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>b>>s>>r;
init();
int u, v, l;
rep(i,1,r){
cin>>u>>v>>l;
add_e(u, v, head, nxt, to);
cnt--, add_e(v, u, _head, _nxt, _to);
len[cnt] = l;
}
dijkstra(dis, head, nxt, to);
dijkstra(_dis, _head, _nxt, _to);
rep(i,1,b) a[i] = dis[i] + _dis[i];
sort(a+1, a+b+1);
rep(i,1,b) A[i] = A[i-1] + a[i];
ll left = 0, right = Inf, mid;
while(left < right){
mid = (left+right)>>1;
if(cal(mid) <= s) right = mid;
else left = mid+1;
}
cal(left);
cout<< dp[b].fr-left*s-A[b] <<endl;
return 0;
}



