AcWing 355. 异象石

题目链接： AcWing 355. 异象石
题目大意：
一棵大小为 \(n\) 的树，\(m\) 次操作，有三种操作：

1. "\(+x\)"  在节点 \(x\) 处出现了异象石
2. "\(-x\)"  节点 \(x\) 处的异象石消失
3. " \(?\) "  询问在树上将所有异象石连通所需边的最小权值和

\(1\leq n,m\leq 10^5\) ，边权 \(1\leq z\leq 10^9\) 。

思路：
这道题有一个不好想到的结论，类比于树的边权和为 \(dfs\) 经过所有边的权值和的一半，结论如下：
我们按照时间戳从小到大排序，将出现异象石的节点首尾相连排成一圈，则相邻节点的距离之和即为答案的一半。

可以结合这棵树理解一下，黑圈的是出现异象石的节点，粗边即联通异象石的边集：

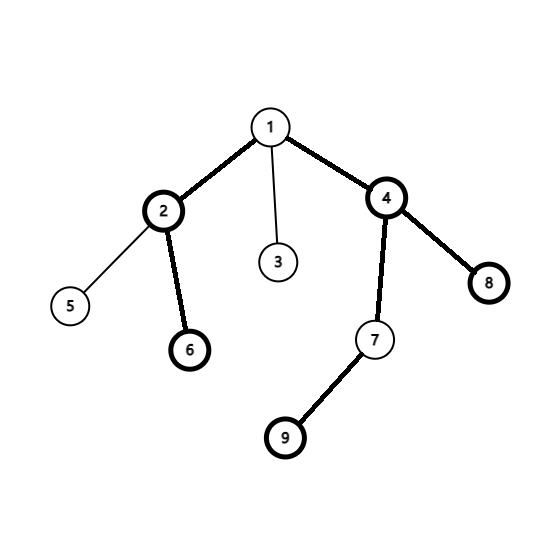
有这个结论之后接下来的就简单了，首先 \(dfs\) 求出 \(dfn_i\) ，使用set维护出现异象石的节点序列，设节点 \(x\) 的前后驱分别为 \(u,v\) ，插入 \(x\) 即 \(ans+=Dis(u,x)+Dis(x,v)-Dis(u,v)\) ，删除类似。
时间复杂度 \(O(nlogn)\) 。

实现细节：

• 倍增求 \(LCA\) 的时候不要把 \(dep\) 和 \(dis\) 搞混了（可能就我会犯这种错误）。
• 注意维护set中的首尾相连，当 set 加入 \(x\) 前是空的时，不用更新 \(ans\) 。

Code：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<set>
#define N 100100
#define LOG 17
#define int long long
using namespace std;
inline int read(){
    int s=0,w=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')s=(s<<3)+(s<<1)+(ch^48),ch=getchar();
    return s*w;
}
int head[N],to[N*2],nxt[N*2];
int cnt,len[N*2];
int dep[N],fa[N][17],dfn[N],rev[N];
int dis[N];
set<int> q;
void init(){
    cnt=-1;
    memset(head,-1,sizeof(head));
}
void add_e(int a,int b,int l,bool id){
    nxt[++cnt]=head[a];
    head[a]=cnt;
    to[cnt]=b;
    len[cnt]=l;
    if(id)add_e(b,a,l,0);
}
void dfs(int x,int fath){
    dfn[x]=++cnt;
    rev[cnt]=x;
    fa[x][0]=fath;
    for(int i=1;i<LOG;i++){
        fa[x][i]=fa[fa[x][i-1]][i-1];
    }
    for(int i=head[x];~i;i=nxt[i]){
        if(to[i]==fath)continue;
        dep[to[i]]=dep[x]+1;
        dis[to[i]]=dis[x]+len[i];
        dfs(to[i],x);
    }
}
int lca(int a,int b){
    if(dep[a]<dep[b])swap(a,b);
    for(int i=16;i>=0;i--)
        if(fa[a][i]&&dep[fa[a][i]]>=dep[b])a=fa[a][i];
    if(a==b)return a;
    for(int i=16;i>=0;i--){
        if(fa[a][i]!=fa[b][i])a=fa[a][i],b=fa[b][i];
    }
    return fa[a][0];
}
int Dis(int a,int b){ 
    return dis[a]+dis[b]-2*dis[lca(a,b)]; 
}
int get(int k,int ud){
    set<int>::iterator it;
    if(ud==0){
        it=q.lower_bound(k);
        if(it==q.begin())return rev[*(--q.end())];
        else return rev[*(--it)];
    }else{
        it=q.upper_bound(k);
        if(it==q.end())return rev[*(q.begin())];
        else return rev[*it];
    }
}
signed main(){
    int n,m;
    int x,y,z;
    cin>>n;
    init();
    for(int i=1;i<n;i++){
        x=read(),y=read(),z=read();
        add_e(x,y,z,1);
    }
    cnt=0;
    dfs(1,0);
    cin>>m;
    char c;
    int in,ans=0;
    for(int i=0;i<m;i++){
        c=getchar();
        while(c!='+'&&c!='-'&&c!='?')c=getchar();
        switch(c){
            case '?':printf("%lld\n",ans/2);break;
            case '+':{
                in=read();
                q.insert(dfn[in]);
                if(q.size()==1)continue;
                int u=get(dfn[in],0),v=get(dfn[in],1);
                ans+=Dis(u,in)+Dis(in,v)-Dis(u,v);
                break;
            }
            case '-':{
                in=read();
                int u=get(dfn[in],0),v=get(dfn[in],1);
                q.erase(dfn[in]);
                ans+=Dis(u,v)-Dis(u,in)-Dis(v,in);
            }
        }
    }
    return 0;
}