POJ1038 Bugs Integrated, Inc.

题目链接: POJ1038 Bugs Integrated, Inc.

题目大意:

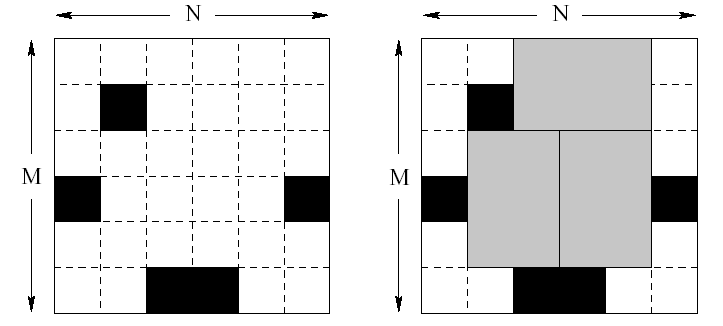
有 \(d\) 张 \(n*m\) 的硅片，上面有一些单元是坏的，求每张硅片最多能生产多少块 \(2*3\) 的芯片。
\(d\leq5\) , \(n\leq150\) , \(m\leq10\).
时限15000ms，空间限制30000kb

思路：

芯片的长度为3，则需要记录前两层的状态，考虑三进制状压 \(dp[i][j]\) 为到了第\(i\)行，此行状态为\(j\)时最多可放多少芯片，为了统计放了几块芯片，我们要记录当前行往上能不能放得下一块芯片，对于状态\(j\)的每一位\(j_k\)：

• \(j_k=0\) : \(a[i-1][k]\) 和 \(a[i][k]\) 都没有放东西
• \(j_k=1\) : \(a[i-1][k]\) 放了东西，\(a[i][k]\) 没有放
• \(j_k=2\) : \(a[i][k]\) 放了东西（此时 \(a[i-1][k]\) 状态不重要）

DP的时候记录 \(P\) 和 \(Q\) 数组为当前行和上一行的状态，dfs向下一行转移。
时间复杂度 \(O(d*C*m*3^m)\)，\(C\) 为dfs转移的时间复杂度，\(m=10\)时 \(C\) 的上限为\(280\)，由于这道题卡空间（约为29Mb），DP要滚动转移。

Code:

#include<iostream>
#include<cstring>
#define N 11
#define M 151
using namespace std;
int pow[N],dp[2][60000];
bool map[M][N];
int n,m;
int P[N],Q[N],cur;
void init(){
    memset(map,true,sizeof(map));
    memset(dp,-1,sizeof(dp));
}
bool Max(int &a,int b){
    if(a>=b)return false;
    a=b;return true;
}
int trois_dix(int C[]){
    int ret=0;
    for(int i=0;i<m;i++)ret=ret*3+C[i];
    return ret;
}
void dix_trois(int* C,int num){
    for(int i=m-1;i>=0;i--,num/=3)*(C+i)=num%3;
}
void print(int x){
    int R[N];
    dix_trois(R,x);
    for(int i=0;i<m;i++)cout<<R[i];
}
void dfs(int x,int y,int num){
    if(y>=m)return;
    int cur=x%2,nxt=(x+1)%2;
    Max(dp[nxt][trois_dix(Q)],dp[cur][trois_dix(P)]);
    if(y<m-1&&(P[y]|P[y+1]|Q[y]|Q[y+1])==0){
        Q[y]=Q[y+1]=2;
        Max(dp[nxt][trois_dix(Q)],num+1);
        dfs(x,y+2,num+1);
        Q[y]=Q[y+1]=0;
    }
    if(y<m-2&&(Q[y]|Q[y+1]|Q[y+2])==0){
        Q[y]=Q[y+1]=Q[y+2]=2;
        Max(dp[nxt][trois_dix(Q)],num+1);
        dfs(x,y+3,num+1);
        Q[y]=Q[y+1]=Q[y+2]=0;
    }
    dfs(x,y+1,num);
}
int main(){
    int t,a,b,k;
    pow[0]=1;
    for(int i=1;i<N;i++)pow[i]=pow[i-1]*3;
    cin>>t;
    while(t--){
        cin>>n>>m>>k;
        init();
        for(int i=0;i<k;i++){
            cin>>a>>b;
            map[a-1][b-1]=false;
        }
        int ans=0;
        dp[0][pow[m]-1]=0;
        for(int i=0;i<n;i++){
            memset(dp[(i+1)%2],-1,sizeof(dp[(i+1)%2]));
            for(int j=0;j<pow[m];j++){
                if(dp[i%2][j]==-1)continue;
                dix_trois(P,j);
                for(int k=0;k<m;k++){
                    Q[k]=max(0,P[k]-1);
                    if(!map[i][k])Q[k]=2;
                }
                dfs(i,0,dp[i%2][j]);
            }
        }
        for(int i=0;i<pow[m];i++)
            Max(ans,dp[n%2][i]);
        cout<<ans<<endl;
    }
    return 0;
}