Numpy 学习笔记
Numpy 基础
- Numpy 是 Python 科学计算的基础,学会如何创建、读取、更改向量数据。
创建向量有许多方法,举例说明:
import numpy as np
print(np.array([2,3,4])) # 可以从列表转换而来,np.array 会尝试为数组推断出一个较为合适的数据类型
[2 3 4]
print(np.zeros( (3,4) , dtype=np.int32)) # zeros 可以创建指定长度或形状的全 0 数组
[[0 0 0 0]
[0 0 0 0]
[0 0 0 0]]
print(np.ones( (2,3,4), dtype=np.float )) # ones 可以创建指定长度或形状的全 1 数组,可以指定 dtype
[[[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]]
[[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]]]
print(np.empty( (2,3) )) # empty 可以创建一个没有任何具体值的数组,
[[ 0. 0. 0.]
[ 0. 0. 0.]]
print(np.arange( 10, 30, 5 )) # arange 是 Python 内置函数 range 的数组版,第三个参数是步长
[10 15 20 25]
print(np.linspace( 0, 2, 9 )) # 同 arrange 类似,只是第三个参数表示要生成的数组元素个数
[ 0. 0.25 0.5 0.75 1. 1.25 1.5 1.75 2. ]
np.zeros((2,3)) # 创建一个二维数组,注意要加括号
array([[ 0., 0., 0.],
[ 0., 0., 0.]])
np.random.normal(10,3,(2,4)) # 二维数组元素来自于期望为 10,标准差为 3 的正态分布
array([[ 9.05422825, 15.64840644, 8.10973337, 14.19151934],
[ 7.25610522, 13.53550744, 8.62793042, 16.15319148]])
np.logspace 这种比较少用的就不提了,感兴趣的可自行查询。随机数生成的方法是比较常用的:
np.random.randn(5) # 从标准正态分布中生成 5 个元素
array([ 0.12789087, 0.82489732, -1.86115425, 0.50760795, -0.3306407 ])
norm10 = np.random.normal(10,3,5) # 从期望为 10,标准差为 3 的正态分布中生成 5 个元素
norm10
array([ 9.60796679, 11.27292882, 10.80855564, 12.13837214, 10.25883022])
np.arange(8).reshape(2,4) # 一维数组可以通过 reshape 转成二维数组
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
读取向量:
arr = np.arange(10) # 一维数组
print(arr)
[0 1 2 3 4 5 6 7 8 9]
print(arr[2])
2
print(arr[2:4])
[2 3]
arr2d = np.array([[1,2,3],[4,5,6],[7,8,9]]) # 二维数组
print(arr2d[2])
[7 8 9]
print(arr2d[0][2])
3
print(arr2d[0, 2]) # 该访问方式同上面是等价的
3
print(arr2d[arr2d<5]) # 还可以指定截取符合条件的数据,也叫逻辑索引
[1 2 3 4]
更改向量:
arr = np.arange(10)
arr[5:8] = 12 # 可以直接修改
print(arr)
[ 0 1 2 3 4 12 12 12 8 9]
arr_slice = arr[5:8]
arr_slice[1] = 12345 # 也可以通过切片来修改
print(arr)
[ 0 1 2 3 4 12 12345 12 8 9]
arr[arr>10] = 0 # 通过逻辑索引修改
print arr
[0 1 2 3 4 0 0 0 8 9]
- 思考 np.array 和 list 有什么不同。
第一个不同,在高维数组中,numpy.array 支持比 list 更多的索引方式。举例说明:
a = [[1, 2 , 3],[4, 5, 6]]
import numpy as np
b = np.array(a)
print type(a)
print a
print type(b)
print b
<type 'list'>
[[1, 2, 3], [4, 5, 6]]
<type 'numpy.ndarray'>
[[1 2 3]
[4 5 6]]
print a[1][2]
print a[1][:]
6
[4, 5, 6]
print a[1,2] # Wrong
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-60-9da16148905d> in <module>()
----> 1 print a[1,2]
TypeError: list indices must be integers, not tuple
print a[1, :] # Wrong
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-61-f921c5f2e22f> in <module>()
----> 1 print a[1, :]
TypeError: list indices must be integers, not tuple
print b[1][2]
print b[1][:]
print b[1, 2]
print b[1, :]
6
[4 5 6]
6
[4 5 6]
第二个不同,list 的元素可以是任何对象,而 np.array 的所有元素必须是相同类型的。比如当 list 和 np.array 存储的都是数值元素时,list 可以修改其中元素为字符串,但 np.array 就不行,要报错。
lst = [1,2,3,4,5,6]
arr = np.array(lst)
lst[-1] = 'openmind'
lst
[1, 2, 3, 4, 5, 'openmind']
arr[-1] = 'openmind'
arr
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-121-da05f2764aba> in <module>()
----> 1 arr[-1] = 'openmind'
2 arr
ValueError: invalid literal for long() with base 10: 'openmind'
list 所保存的是对象的指针。这样为了保存一个简单的[1,2,3],需要有3个指针和三个整数对象。对于数值运算来说这种结构显然比较浪费内存和CPU计算时间。np.array 是存储单一数据类型的多维数组,运算效率要高。
第三个不同,np.array 的大小是创建时就指定的,不能改变大小,而 list 可以随时添加元素进去,list 有 append 函数。在实际使用中会经常遇到运行前不知道数组大小的情况,这时候就可以初始化 list 为空,然后在运行中根据需要添加元素进去,最后计算时可把 list 转为 np.array 以提高效率。可见,list 和 np.array 有合作的空间。
- 如何使用 mask 方法快速截取数据。
mask 是一种按条件提取数组中数据的方法。举例即可说明,如下例要提取向量中的偶数。
import numpy.ma as ma
import numpy as np
a = np.arange(10)
a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
mask = a%2==0
mask
array([ True, False, True, False, True, False, True, False, True, False], dtype=bool)
a[mask]
array([0, 2, 4, 6, 8])
Array 高维数组操作
- 思考 view 和 copy 的区别。
view 是浅复制,copy 是深复制。什么意思呢?
浅复制就是不复制,view 创建的新的数组对象指向同一数据,对 view 上的任何修改都会直接反映到源数组上。数组切片就是原始数组的视图。举个例子就明白了。
arr = np.arange(10)
arr_slice = arr[5:8]
arr_slice[1] = 12345
arr
array([ 0, 1, 2, 3, 4, 5, 12345, 7, 8, 9])
看到了吧,对 arr_slice[1] 的修改就是对 arr 的修改,因为 arr_slice 是 arr 的视图。
reshape 也是一种 view,修改 reshape 后的数组内容会影响到原数组。
arr1 = np.arange(8)
arr2 = arr1.reshape(2,4)
arr2[0,0]=1234
arr1
array([1234, 1, 2, 3, 4, 5, 6, 7])
深复制才是真正的复制,copy 就是生成了数组切片的一个份副本。对该副本的操作就不会影响到原数组的值。
arr_copy = arr.copy()
arr_copy[1] = 56789
arr
array([ 0, 1, 2, 3, 4, 5, 12345, 7, 8, 9])
可见,对 copy 值的修改并没有影响原数组。
- np.array 还有哪些属性和方法?
属性:dtype, size, ndim, shape, nbytes
创建 np.array 时,如果没有显式指定,np.array 会为新建的数组推断出一个较为合适的数据类型,中途如果要修改 dtype 就只有通过 astype 方法显式转换 dtype。
arr = np.array([1, 2, 3, 4, 5])
print arr.dtype
arr[0] = 3.1415
print arr.dtype
float_arr = arr.astype(np.float64)
print float_arr.dtype
int64
int64
float64
一元通用函数:abs, fabs, sqrt, square, exp, log, log10, sign, ceil, floor, cos, cosh, sin, sinh, tan, tanh……
二元通用函数:add, subtract, multiply, divide, power, maximum, minimum, mod, copysign, greater, less, equal……
arr1 = np.arange(4)
arr2 = np.arange(10,14)
print(arr1,'+',arr2,'=',arr1+arr2) # 对应元素相加
(array([0, 1, 2, 3]), '+', array([10, 11, 12, 13]), '=', array([10, 12, 14, 16]))
print(arr1,'*',arr2,'=',arr1*arr2) # 注意这里的乘是两数组中对位元素相加,跟线性代数中的矩阵乘法不同
(array([0, 1, 2, 3]), '*', array([10, 11, 12, 13]), '=', array([ 0, 11, 24, 39]))
基本数组统计方法:sum, mean, std, var, min, max, argmin, argmax, cumsum, cumprod
arr = np.arange(12).reshape(3,4) # 看下二维数组,可以按行求和,可以按列求和
print arr
print arr.sum(axis = 0) # 求每一列的和,即按列求和,相当于抹掉了行维度
print arr.sum(axis = 1) # 求每一行的和,即按行求和,相当于抹掉了列维度
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[12 15 18 21]
[ 6 22 38]
数组集合运算:unique(x), intersect1d(x), union1d(x,y), in1d(x,y), setdiff1d(x,y), setxor1d(x,y)
数组文件输入输出:save, load, loadtxt, genfromtxt
线性代数:diag, dot, trace, det, eig, inv, pinv, qr, svd, solve, lstsq
随机数生成:seed, permutation, shuffle, rand, randint, randn, binomial, normal, beta, chisquare, gamma, uniform
- 理解什么是 broadcasting?如何使用?
广播(broadcastring)是指不同形状的数组之间算术运算的执行方式。例如,将标量值跟数组合并时就会发生最简单的广播。
arr = np.arange(5)
4 * arr
array([ 0, 4, 8, 12, 16])
低维变量遇到高维变量会自动补全,如上面就是把 4 复制成一个同 arr 一样的含 5 个元素的一维向量,然后对位元素相乘,也可以说标量值 4 被广播到了 arr 的所有元素上。
再比如数据分析中经常用到的距平化处理,对数组的每一列减去平均值。
arr = np.random.randn(4,3)
arr - arr.mean(0)
array([[-0.00186826, 0.36242026, 1.20839815],
[ 1.47094699, 1.02999549, -0.79207756],
[-1.55548229, 0.27482805, -1.05206272],
[ 0.08640356, -1.6672438 , 0.63574213]])
可见,所谓广播,也就是把对矩阵的操作广播到每个元素的操作。
如果列向量遇到行向量会如何呢?
np.arange(3).reshape((3, 1)) + np.arange(3)
array([[0, 1, 2],
[1, 2, 3],
[2, 3, 4]])
一图胜千言,看了下图,广播的规则就一目了然了。
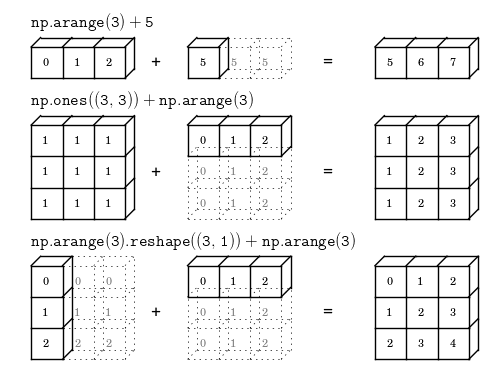
只要遵循一定的规则,低维度的值是可以被广播到数组的任意维度的。
只要记住,遇到不同维度的运算,先对低维度补全,补全到相同的维度再计算,就不会迷惑。
Numpy 中的线性代数
- 如何计算向量、矩阵相乘?
Numpy 提供了一个用于矩阵乘法的 dot 函数。先来看下向量相乘:
v1 = np.array([1,2,3]) # 先来看下向量相乘
v2 = np.array([2,3,4])
print np.dot(v1,v2)
print np.dot(v1.T,v2)
print np.dot(v1,v2.T)
print np.dot(v1.T,v2.T)
print v1
print v1.T
20
20
20
20
[1 2 3]
[1 2 3]
由上可见,在 Numpy 中,向量是不分行向量和列向量的,转置对向量不起作用,这点跟预想的不一样。要注意的是,reshape 不能转置向量,reshape 只是改变数组的形状。
print v1.reshape(3,1) # 试图通过 reshape 转置向量
print v1
np.dot(v1.reshape(3,1),v1) # 失败的线性相乘
[[1]
[2]
[3]]
[1 2 3]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-174-ed17a869fdc6> in <module>()
1 print v1.reshape(3,1)
2 print v1
----> 3 np.dot(v1.reshape(3,1),v1)
ValueError: shapes (3,1) and (3,) not aligned: 1 (dim 1) != 3 (dim 0)
再来看向量和矩阵相乘。
v1 = np.array([2, 3, 4])
A = np.arange(6).reshape(2,3)
print np.dot(A, v1) # 2 行 3 列的矩阵乘 3 行 1 列的向量应等于 2 行 1 列的矩阵
print np.dot(A, v1.T) # 看结果再次证明,Numpy 是不分行向量和列向量的
B = np.arange(6).reshape(3,2)
print np.dot(v1, B) # 1 行 3 列的向量乘 3 行 2 列的向量等于 1 行 2 列的向量
[11 38]
[11 38]
[22 31]
可以这么看,当矩阵乘向量,即向量在后时,那么向量就是列向量;当向量乘矩阵,即向量在前时,那么向量就是行向量。
矩阵和矩阵相乘,只要符合维度要求即可。
x = np.array([[1,2,3],[4,5,6]]) # 2 行 3 列的矩阵
y = np.array([[6.,23],[-1,7],[8,9]]) # 3 行 2 列的矩阵
x.dot(y) # 得 2 行 2 列的矩阵
[[1 2 3]
[4 5 6]]
array([[ 28., 64.],
[ 67., 181.]])
- 如何从文件中读取数据?
前面都是在内存空间中计算 np.array,那么它怎么和磁盘空间进行输入输出交互呢?有两种读写方式,一种是 Text 模式,一种是 Binary 模式。
Text 模式是可以把数组以字符串的方式存到文本文件中,人们用编辑器打开文件读得懂,也可以手动修改。只能用于一维和二维数组。
Binary 模式是以二进制存储,跟内存中格式一模一样,包含数组的大小和维度,没有信息损失,原模原样存储自然效率高。但人们不能读懂,无法编辑。
arr = np.arange(10).reshape(2,5)
np.savetxt('test.out',arr,fmt='%2e',header='My dataset') # 以 Text 模式存储
!cat test.out
# My dataset
0.000000e+00 1.000000e+00 2.000000e+00 3.000000e+00 4.000000e+00
5.000000e+00 6.000000e+00 7.000000e+00 8.000000e+00 9.000000e+00
arr2 = np.loadtxt('test.out') # 以 Text 模式读取
print(arr2)
[[ 0. 1. 2. 3. 4.]
[ 5. 6. 7. 8. 9.]]
np.save('test.npy', arr2) # 以 Binary 模式存储
!cat test.npy # 可以看到 Binary 模式存储的内容好像一团乱码
�NUMPY F {'descr': '<f8', 'fortran_order': False, 'shape': (2, 5), }
�? @ @ @ @ @
@ @ "@
arr2n = np.load('test.npy') # 以 Binary 模式读取
print arr2n
[[ 0. 1. 2. 3. 4.]
[ 5. 6. 7. 8. 9.]]
通过 np.savez 可以将多个数组保存到一个压缩文件中,将数组以关键字参数的形式传入即可。
np.savez('test.npz', arr, arr2) # 以 Binary 模式存储多个数组
arrays = np.load('test.npz')
arrays.files
!cat test.npz # 一团乱码
� � arr_1.npy�NUMPY F {'descr': '<f8', 'fortran_order': False, 'shape': (2, 5), }
�? @ @ @ @ @
@ @ "@PK l��H x
�� � arr_0.npy�NUMPY F {'descr': '<i8', 'fortran_order': False, 'shape': (2, 5), }
� � �� arr_1.npyPK l��H x
�� � ��� arr_0.npyPK n �
读取文件还有 pandas 的 read_csv 和 read_table 函数,后面的课程会讲到。
小结
Numpy 提供了 Array 这种数据结构,提供了所有 Python 环境中数值计算的底层支持,Array 使向量化计算更为容易,Array 有大量方便的内置函数。
补充阅读
-
利用 Python 进行数据分析 第 4 章
-
Numerical Python 第 2 章
-
Scipy Lecture 第 3 章



