机器学习笔记—主成分分析
在介绍因子分析时,我们把数据 x∈Rn 建模在 k 维子空间上,k<<n。我们假设每个点 x(i) 是这样生成的:先从 k 维高斯多元高斯分布中采样得到 z(i),再通过计算 μ+Λz(i) 将 z 映射到 n 维空间,给 μ+Λz(i) 增加协方差噪声 ψ,得到 x(i)。因子分析是基于概率模型,参数估计使用了迭代式 EM 算法。
本文介绍主成分分析方法,即 PCA,尝试找出数据依赖的子空间。但 PCA 会做得更直接,只需要用到向量计算,不需要使用 EM。
设有 m 种不同汽车的属性数据 {x(i),i=1,...,m},如最大速度、转弯半径等,其中 x(i)∈Rn(n<<m)。但我们不知道的是,有两个属性 x 和 x,都表示汽车的最大时速,只是一个以英里为单位,一个以公里为单位。所以,这两个属性几乎是线性依赖的,只是因为取整不同会有一点小区别。所以,数据其实几乎是依赖于 n-1 维子空间的,我们怎么才能检测或者去除这种冗余呢?
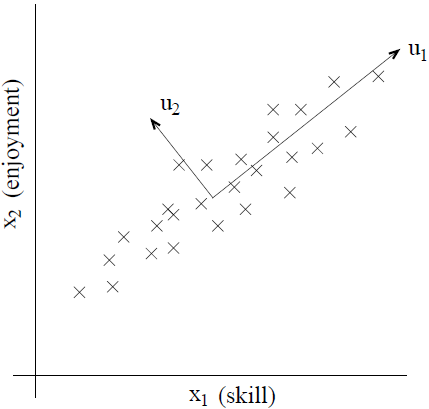
举一个自然点的例子,有无线电控制直升机的驾驶员数据,其中 x1(i) 表示驾驶员 i 的技能程度,x2(i) 表示他有多喜欢飞行。因为无线电控制的直升飞机很难飞行,所以只有最愿意投入的学生,真正喜欢飞行,才能成为好的驾驶员。所以,两个属性 x1 和 x2 是强相关的。实际上,我们看到斜线轴方向捕捉到了人们的飞行本质,在该斜线轴上只有一点噪声。怎么才能自动计算 u1 方向呢?
我们将简单介绍 PCA 算法,在运行 PCA 算法之前,先对数据进行预处理,归一化均值和方差。
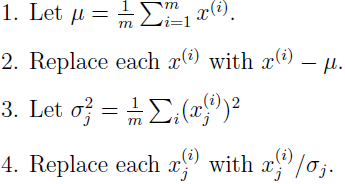
现在,怎么来计算变化的主轴 u,也就是数据近似呈现的方向。根据观察,在跟 u 相关的方向上,数据映射到该方向上后的方差最大。直觉上,方差越大,信息量也越大。
考虑如下数据集,已经执行了归一化。
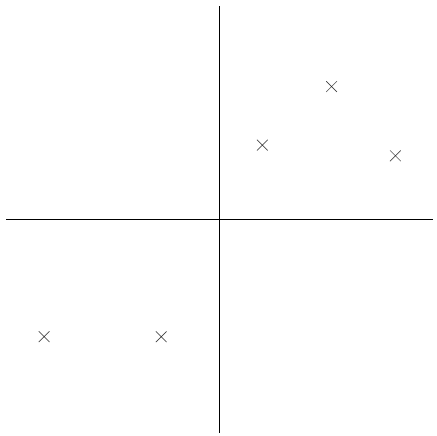
现在假设 u 是下图所示方向,圆圈表示原始数据到该线上的映射点。
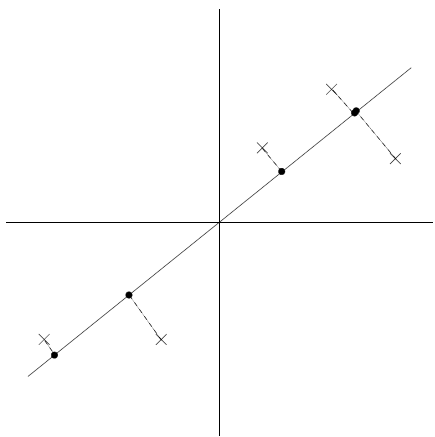
可以看到映射数据有较大的方差,点趋向于远离原点。相反,如果取下列方向:
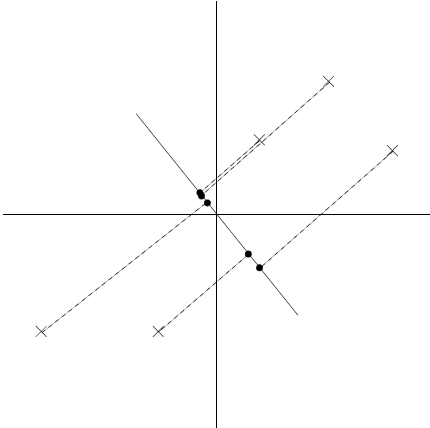
映射点的方差就明显要小得多,更靠近原点。
我们希望能自动找到上面两幅图的第一幅的 u。给定单元向量 u 和点 x,x 在 u 上的映射的长度为 xTu。所以,为最大化映射的方差,我们要选择单元向量 u,以最大化
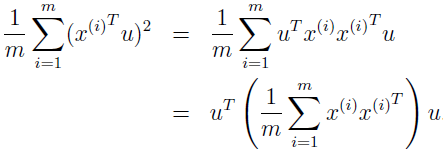
该式有一个约束条件,|u|2=1,Σ 正好是数据的经验协方差矩阵。这个最大化问题的解 u 就是 Σ=(1/m)ΣxxT 的特征向量。这是如何得到的呢?
使用拉格朗日方程来求解该最大化问题,则:
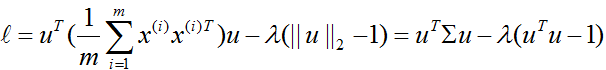
对 u 求导,得
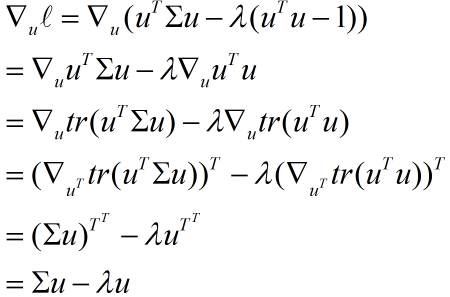
令导数为 0,可知 u 就是 Σ 的特征向量。
如果我们要将数据映射到 k 维子空间(k<n),我们应该选择 Σ 最大的 k 个特征向量 u1,u2,...,uk。
现在以 x(i) 为基础,我们只需要计算相关向量:
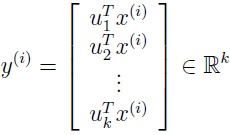
y(i) 给出了一个 k 维的 x(i) 的近似。PCA 也因为被称为降维算法。向量 u1,...,uk 被称为数据的 k 个主成分。
PCA 有许多应用。首先是压缩,用低维的 y(i) 表示 x(i),如果能将高维数据压缩到 2 或 3 维,我们就可以画出 y(i) 以可视化数据。例如如果能把汽车数据压缩到 2 维,就可以看出哪些汽车是类似的,聚集在一块的;还有预处理,在运行监督学习算法之前先降维,除了计算上的好处,还能降低假设的复杂度,防止过拟合;PCA 还可用于降低噪声,例如从飞行技能和飞行享受的数据噪声中提取出本质。
参考资料:
[1] http://cs229.stanford.edu/notes/cs229-notes10.pdf
[2] http://blog.csdn.net/stdcoutzyx/article/details/37568225



