机器学习笔记—支持向量机(1)
在逻辑斯特回归中:

当 hθ(x) ≥ 0.5 即 θTx ≥ 0 时,输出为 1, θTx 越大,hθ(x)=p(y=1|x;w,b) 越大。
在支持向量机中,我们换下符号,不再使用 θ,而是用 w,b。分类器为:
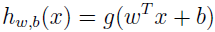
当 wTx+b≥0 时,g(wTx+b)=1,不然 g(wTx+b)=-1。可以看出,这里不再像逻辑斯特回归一样要去计算概率,而是直接根据 wTx+b 是否大于 0 就判断输出是否为 1。
给定训练集 (x(i),y(i)),定义训练例子的函数间隔:
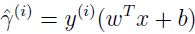
训练集的函数间隔:
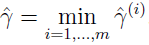 训练例子的几何间隔:
训练例子的几何间隔:
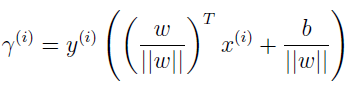
训练集的几何间隔:
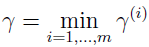
支持向量机的目标就是在训练集上寻找一个决策边界,能够最大化几何间隔。

最大化 1/||w|| 和最小化 ||w||2 等同。所以上面最优化问题可以转化为:
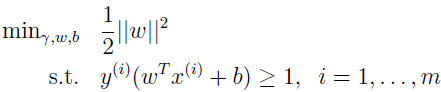
上式有个凸二次目标函数和线性约束,可以用商业的 QP(二次规划)代码求解,解出的答案就是一个最优间隔分类器。
下面我们要讲一下,如何解这个最优化问题。虽然有现成的软件可以解这个问题,但因为下面介绍核概念时还是要涉及这个,所以我们这里就把这个解的过程好好理一下。
上面最优化问题的求解,用的就是拉格朗日对偶。所以这里先把拉格朗日对偶介绍清楚。
先暂时抛开 SVM 和最大间隔分类器,来解约束优化问题。
考虑如下问题:

使用朗格朗日乘数法可解,定义拉格朗日函数为:
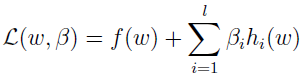
这里 βi 被称为拉格朗日乘子,设置 L 的偏导为 0。
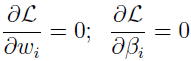
解出 ω 和 β,即得解。
下面我们将此推广到有不等式约束的约束优化问题。这里并不详细介绍朗格朗日对偶理论,只给出主要思想和结果,然后应用到最优间隔分类器的最优化问题。
考虑如下原始优化问题:
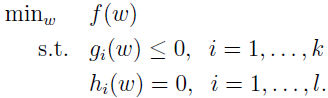
为解上面问题,需定义广义拉格朗日函数:
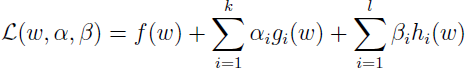
其中 αi 和 βi 是拉格朗日乘子。定义如下函数:
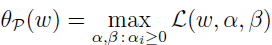
其中下标 Ρ 表示原始(primal),ω 是给定的,当 ω 违反一些原始约束时(如有些 i 的 gi(ω)>0 或者 h(ω)≠0),那么

相反,如果 ω 满足约束,那么 θP(ω)=f(ω) ,所以
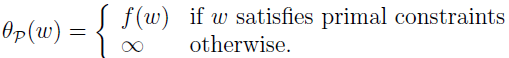
所以,当 ω 满足约束时,θP 跟我们原始优化问题的目标一样,不满足约束时,θP 就为正无穷。所以,最小化问题
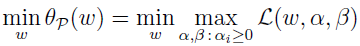
跟我们的原本的问题一样,有相同的答案。定义目标的最优值为 p*=minω(θP(ω)) 。
再来看另一个稍有不同的问题:
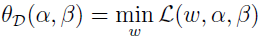
这里的下标 P 表示对偶(dual)。
对偶最优化问题为: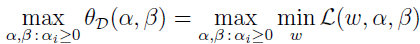
这和我们上面定义的原始问题几乎相同,只是 min 和 max 的位置换了下。定义对偶问题的目标值为 d*=maxα,β:αi≥0(θD(ω))
原始问题和对偶问题有什么关系?显然:
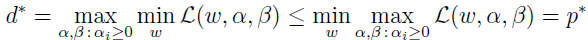
而且,在一定条件下,有 d*=p*。然后,我们就能通过解对偶问题来解原始问题了。
我们来看看这「一定条件」指的是什么。
假设 f 和 gi 是凸函数,hi 是仿射函数,进一步假定约束 gi 是严格可行的,即存在一些 ω,使得对所有的 i,gi(ω)<0。
在以上假设下,一定存在 ω*,α*,β*,使得 ω* 是原始问题的解,α* 和 β* 是对偶问题的解,并且 p*=d*=L(ω*,α*,β*),并且 ω*,α* 和 β* 满足 KKT 条件,如下所示:
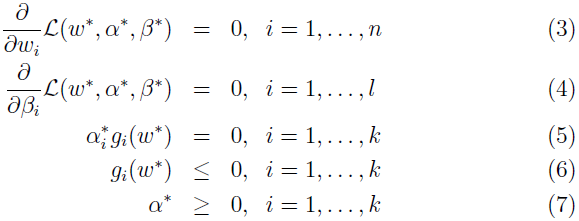
如果 ω*,α* 和 β* 满足 KKT 条件,那么它们也同时是原始和对偶问题的解。
注意看条件(5),被称为 KKT 对偶互补条件。它表示,当 αi*>0 时,gi(ω*)=0。稍后我们会看到,这是 SVM 只有很少几个支持向量的关键。当我们讲到 SMO 算法时,KKT 的对偶互补条件会有一个收敛测试。
之前,我们为了找到最优间隔分类器,提出了下面的最优化问题:
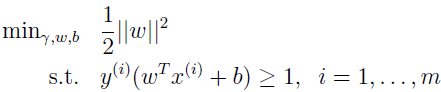 把约束改成下面形式:
把约束改成下面形式:
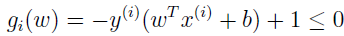
由 KKT 的对偶互补条件可知,αi>0 仅仅是对于函数间隔等于 1 的,这样 gi(ω)=0,在支持向量机的最优化问题中,也就是支持向量。
为我们的最优化问题构建拉格朗日式子。
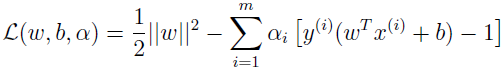
这里只有 αi,没有 βi 拉格朗日乘子,因为只有不等式约束。
先找出问题的对偶形式,固定 α,L 只有 w 和 b 有关,为了得到 θD,我们对 w 和 b 求偏导,并使其等于 0。
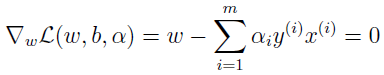
所以

同样,对 b 求偏导得

把上面两式代入拉格朗日式子 L 中得
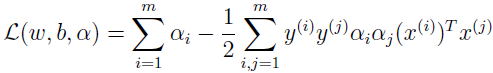
得对偶最优化问题
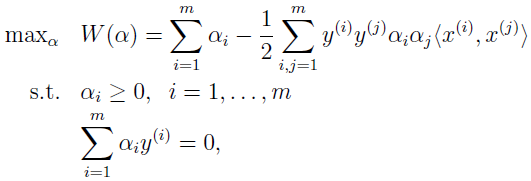
可以验证,该最优化问题是符合 KKT 条件和 p*=d* 的,所以我们可以通过解对偶问题来替代解原始问题。在上面的对偶问题中,还有个以 αi 为参数的最大化问题有待解决。后面会讲解对偶问题的特别算法。假设已经解出,也就是找到了在约束条件下使 W(α) 最大的 α,然后就可以根据上面公式算出 w*,根据原问题,可以找到截距 b 的最优值为
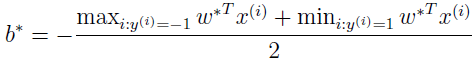
假设已经根据数据集找到模型的参数,现在来了一个新数据 x 要做预测,我们要计算 wTx+b,大于等于 0 时 y=1。
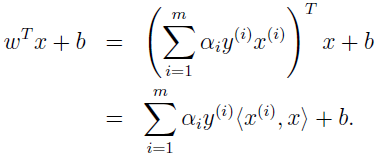
所以,一旦我们找到了 αi,要做预测分类只需计算 x 和训练数据的内积即可。除了支持向量,其它 αi 都为 0。上式中许多项都为 0,所以做预测时,我们只需计算 x 和支持向量的内积。
参考资料:
1、http://cs229.stanford.edu/notes/cs229-notes3.pdf



