机器学习笔记—生成学习
目前我们主要介绍了建模 p(y|x;θ) 的学习算法,即关于给定 x 后 y 的条件分布。例如,Logistic 回归把 p(y|x;θ) 建模为 hθ(x)=g(θθx),其中 g 是 sigmoid 函数。本文将介绍一种不同类型的算法。
考虑一个分类问题,学习根据动物的特征区分大象(y=1)和狗(y=0)。给定一个训练集,像 Logistic 回归或者感知机这种算法会试图找到一条直线,即决策边界,把大象和狗区分开,然后,来一个新的动物,就可以根据它落在哪个边界内,就属于哪种动物。
有一种不同的方法,首先,看看大象,建立一个大象的特征模型,再看看狗,建立一个狗的单独模型。最后,来了新动物,就分别跟大象和狗的特征比对,看跟哪个更像,就是哪个。
直接学习 p(y|x) 的算法(如 Logistic 回归),或者学习从输入空间 X 到 标签 {0,1} 的映射的算法(如感知机算法),被称为判别学习算法。本文我们介绍的算法是试图建模 p(x|y) 和 p(y),被称为生成学习算法。例如,如果 y 表示一个数据是狗(0),或者大象(1),那么 p(x|y=0) 就建模了狗的特征分布,p(x|y=1) 建模了大象的特征分布。
建模 p(y) 和 p(x|y) 后,我就能使用贝叶斯规则来导出后验概率:
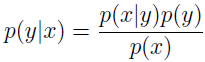
其中,分母 p(x)=p(x|y=1)p(y=1)+p(x|y=0)p(y=0)。实际上,如果计算 p(y|x) 只是为了预测分类,那我们就不必计算分母。因为:
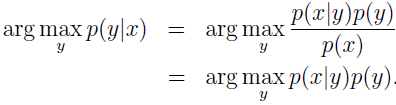
生成学习是一种跟判别学习不同的算法。
1、高斯判别分析
有个分类问题,输入特征 x 是连续值的随机向量,就可以用高斯判别分析(GDA)模型,即用多元正态分布来建模 p(x|y)。
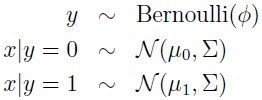
写出分布为:
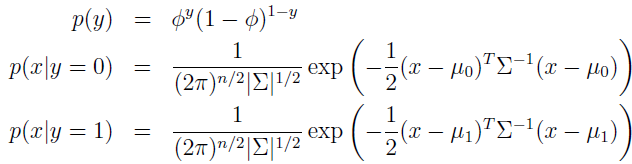
这里,模型参数是 Φ、Σ、μ0 和 μ1。(注意虽然有两个均值,但通常方差矩阵都是一样的)数据的 log 似然估计为:
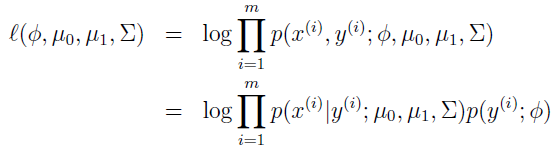
通过调整参数使该 log 似然函数最大化,参数的最大似然估计为:
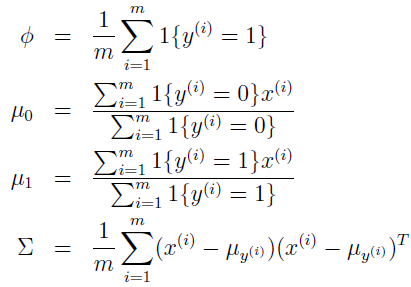
当有新数据时,只需计算 p(x|y)p(y) ,找到使其最大的 y 即完成分类。
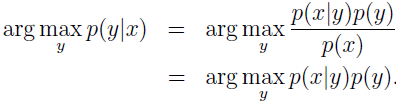
2、朴素贝叶斯
特性向量 x 的元素是离散值。
假设有一个训练数据集,邮件集合,被标注为垃圾邮件和非垃圾邮件。我们要建一个邮件过滤器,根据邮件特征来判断是否垃圾邮件。
我们用特性向量来表示邮件,向量长度等于词典中的单词个数,如果一封邮件包含词典的第 i 个单词,那么就设 xi=1,不然 xi=0。
朴素贝叶斯对条件概率分布作了条件独立性的假设,即给定 y 的条件下,xi 之间是条件独立的。例如,如果 y=1 表示垃圾邮件,“buy” 是2087号单词,“price”是39831号单词。“buy”有没有出现在邮件中,跟“price”有没有出现在邮件中没关系。记作:p(x2087|y)=p(x2087|y,x39831)。
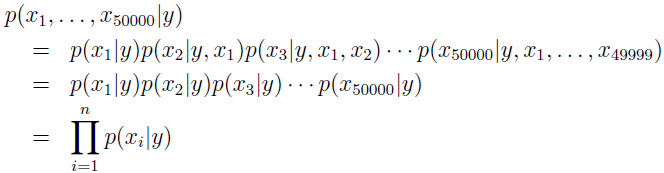
我们模型的参数是 Φi|y=1=p(xi=1|y=1),Φi|y=0=p(xi=1|y=0),跟之前一样,给定训练数据集 {(x(i),y(i));i=1,...,m},数据的联合分布概率为:

最大化该似然函数,Φy、Φi|y=1 和 Φi|y=0 的最大似然估计如下,求解过程可见参考资料2。
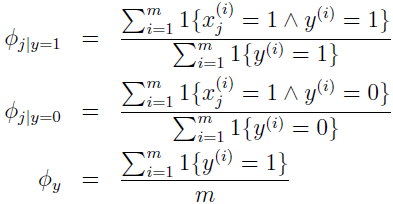
当有新的数据时,就计算:
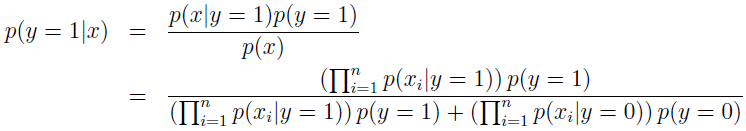
然后选择最高后验概率的 y 值。
对于许多分类问题,上面的朴素贝叶斯已经能工作很好了,对于文本分类,还有一个相关的模型可以运行得更好。
在特定的文本分类情境下,上面介绍的朴素贝叶斯,使用的是多元伯努利事件模型, 在这个模型中,邮件生成的方式是,首先根据先验概率 p(y) 随机决定是发垃圾邮件还是非垃圾邮件,然后再扫描词典,根据后验概率 p(xi=1|y)=Φi|y 决定是否包含单词 i。所以,一条信息的概率为 p(y)∏ni=1p(xi|y)。
这里介绍的不同的模型,被称为多项式事件模型。这个模型使用了不同的标识和特征集合来表示邮件。xi 表示邮件中的第 i 个单词的标志,所以,这里的 xi 是个整数,取值 {1,...,|V|},其中 |V| 是词典大小。一个邮件的 n 个词现在表示成一个 n 维的向量 {x1,x2,..,xn},n 会随着文件不同而变化。
在多项式事件模型中,假设生成一封邮件的方式,还是先根据先验概率 p(y) 确定是否垃圾邮件,然后邮件写作者根据后验概率 p(x1|y) 的多项式分布中选择第一个词 x1,然后从同一个分布中选择 x2,类似的 x3,x3 等等,直到邮件的所有 n 个词生成。所以该信息的概率是 p(y)∏ni=1p(xi|y) ,形式跟多元伯努利事件模型的概率看起来一样,但表达的含义已经不一样了,xi|y 现在是一个多项式分布,而不是伯努利分布。
参数 Φy=p(y),Φi|y=1=p(xj=i|y=1),Φi|y=0=p(xj=i|y=0)。注意我们的假设 p(xj|y) 对于所有的 j 都是一样的,也就是说,这个分布只决定于是哪个单词,而与单词在邮件中所在的位置无关。
给定训练数据集 {(x(i),y(i));i=1,...,m},x(i)=(x1(i),x2(i),...,xni(i)),这里 ni 表示训练集中第 i 封邮件的单词个数。数据的似然函数为:
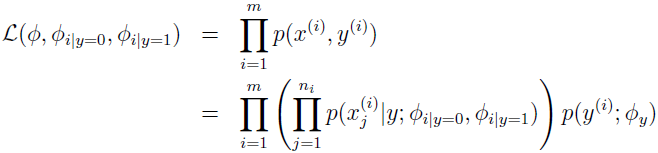
最大化该似然函数,参数的最大化似然估计为:
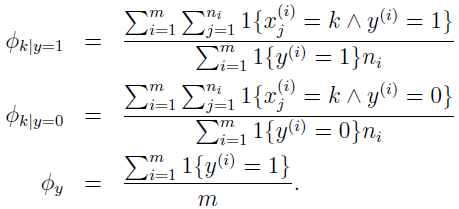
在估计 Φk|y=1 和 Φk|y=0 时,如果要使用 Laplace 平滑,给分子加 1,分母加上 |V|。
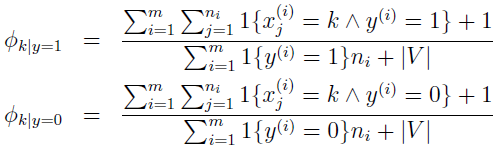
如果不是必需最好的分类算法,那朴素贝叶斯就非常好了,它通常是首选,因其简单和易执行性。
问答环节:
(1)怎么把一封邮件编程变成一个向量?
答:先定义个长度为 5000 的向量,初始化为 0,然后根据词典来扫描邮件,假如词典的词汇量为 5000,扫描到邮件中有响应的单词,则向量的该元素置为 1,一直到扫描完整封邮件,表示该邮件的向量即生成。该向量只记录了邮件中出现了哪些单词,而不管单词出现的先后顺序,及出现次数,也不用懂语法规则。
(2)建模 p(x|y) 时,朴素贝叶斯的条件独立假设有什么用?
答:假设 x 是长度为 5000 的向量,每个元素为 0 或 1。假如不作条件独立假设,那 x 的随便哪个元素变一下,就是一个新的向量,一共就有 25000 个可能的向量,每个向量的 p(x|y) 都要通过训练集来计算,这几乎是不可能的。所以我们要做条件独立假设,在给定 y 后,x 的各个元素是相互独立的,即 p(xi|y)=p(xi|y,xj),这样 p(x1,x2,x3|y)=p(x1|y)p(x2|y)p(x3|y),这样就不需要很大的数据集就能建立模型。

参考资料:
1、http://cs229.stanford.edu/notes/cs229-notes2.pdf
2、http://cs229.stanford.edu/materials/ps1.pdf



