Coursera课程《Machine Learning》学习笔记(week2)
1 特征
1-1 什么是特征?
我的理解就是,用于描述某个样本点,以哪几个指标来评定,这些个指标就是特征。比方说对于一只鸟,我们评定的指标就可以是:(a)鸟的翅膀大还是小?(b)鸟喙长还是短?(c)鸟下的蛋是多还是少?等等,这些都能被称之为“鸟”这个样本点的特征。
特征值的数量用“n”来表示。比如我们用一些特征来描述一栋房子,这些特征包括:(a)多少*米?(b)几室几厅?(c)有几层?(d)房子是新还是旧?那么这里就有4个特征,也就是n=4。
1-2 现在我们区分一下符号
(1)m:样本点的数目。
(2)n:特征值的数目。
(3)上标(i):代表了当前样本点是“第几个样本点”,${x}^{(i)}$是一个向量,里面的每一个元素都是用于描述同一个样本点的不同特征。以下图为例,${x}^{(2)}$就是第二个样本点,它是一个四维列向量,这四个元素分别代表:(a)多少*米?(b)几室几厅?(c)有几层?(d)房子是新还是旧?每一个元素都是一个不同的特征。

(4)下标j:指明了“这是该样本点中哪一个特征”。仍以上图为例,有${x_{2}}^{(3)}$,它是第二个样本点的第三个特征,也就是这栋屋子有2层(numbers of floors)。
(2016.6.30记)
2 梯度下降法技巧
2-1 特征缩放(feature scaling)
2-1-1 狭长的椭圆
当两个特征范围差别比较大时,比方说仍用上面房价那个例子,对于某一个样本点,其房子的大小$x_{1}^{(i)}$范围为0~2000,而卧室数目$x_{2}^{(i)}$的范围为1~5,如果我们只用这两个特征来描述这栋房子,那么其hypothesis有:
$h_{\theta }(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}$ (2-1)
其cost函数为:
$J(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$ (2-2)
简单起见,我们假定只有一个样本点,并且忽略掉$\theta _{0}$和label$y$(理解成恰好$\theta _{0}=y$于是刚好一减就没了也未尝不可,总之是为了简化情况),那么这种情况下的cost函数为:
$J(\theta )=\frac{1}{2}(\theta _1x_{1}+\theta _2x_{2})^{2}$ (2-3)
之前我们说过$x_{1}^{(i)}$范围为0~2000,而卧室数目$x_{2}^{(i)}$的范围为1~5,那么不妨令$x_{1}$=2000,$x_{2}$=5。代入式(2-3),得到cost函数:
$J(\theta )=\frac{1}{2}(2000\theta _1+5\theta _2)^{2}$ (2-4)
把这个式子(2-4)用Python画出来:
import numpy as np import matplotlib.pyplot as plt import mpl_toolkits.mplot3d theta1,theta2=np.mgrid[-500:500:20j,-500:500:20j] J_theta=0.5*(2000*theta1+5*theta2)**2 ax=plt.subplot(111,projection='3d') ax.plot_surface(theta1,theta2,J_theta,rstride=1,cstride=1, cmap=plt.cm.hot) ax.contourf(theta1,theta2,J_theta, zdir='z', offset=-2, cmap=plt.cm.hot) ax.set_xlabel('theta1') ax.set_ylabel('theta2') ax.set_zlabel('J_theta') plt.show()
得到这样一幅图,其中theta1-theta2*面上的是“theta1-theta2-J_theta”的轮廓图。
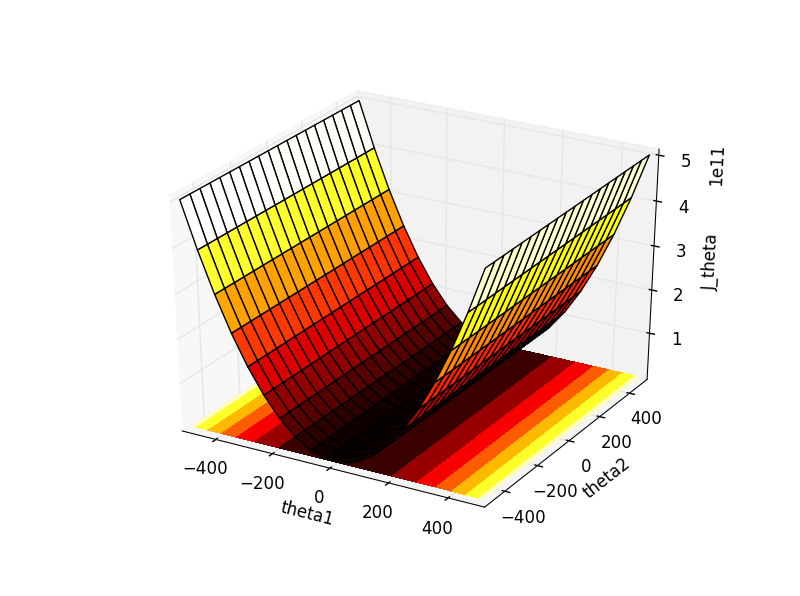
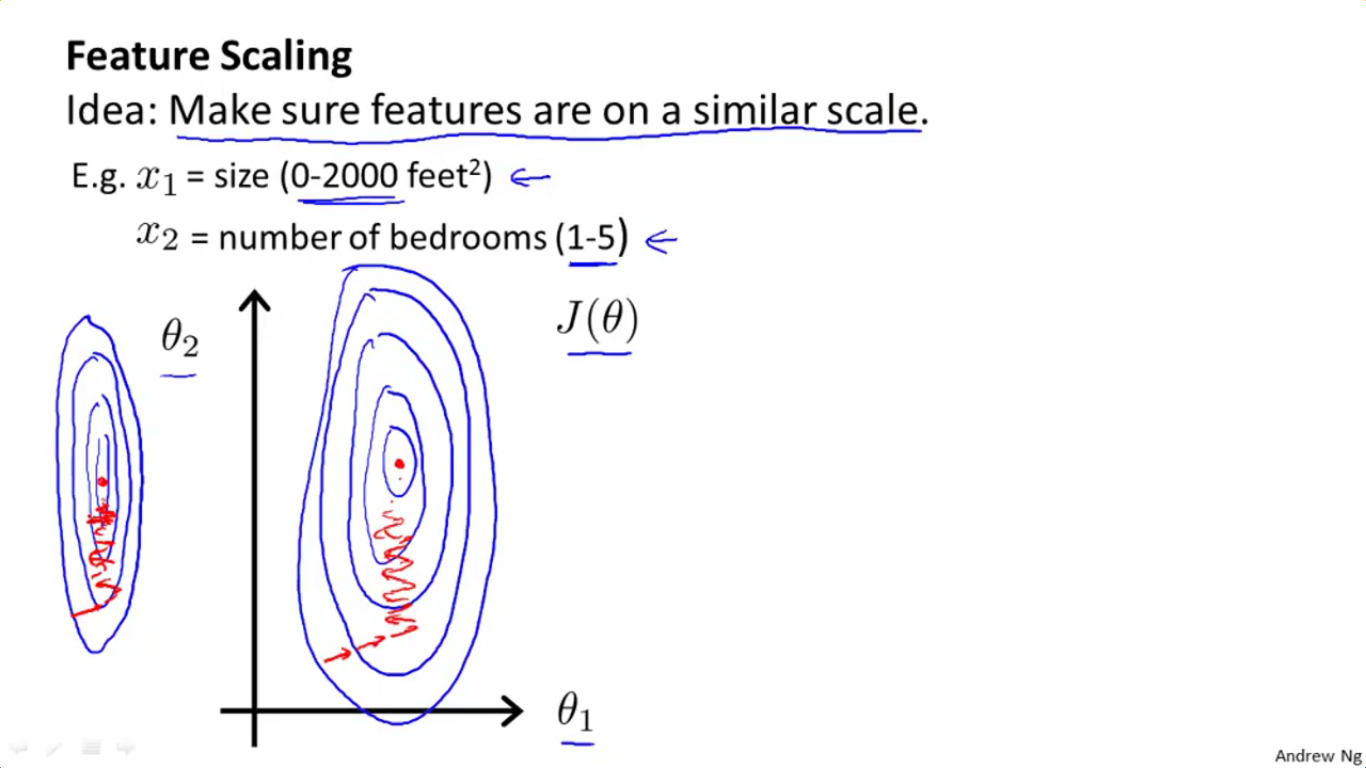
对比一下Ng课件里的这幅轮廓图,我们发现情况是完全吻合的,也就是椭圆沿theta2方向被拉得非常非常长,因此在上面的图中无法一窥椭圆的全貌,各椭圆的侧边*乎是*行的。
上面我们通过Python绘图演示了椭圆确实被拉得很长这一现象。为了进一步理解为什么会沿theta2方向被拉长,我们再绘制一下$J(\theta )=\theta _1^{2}$的图:
import numpy as np import matplotlib.pyplot as plt import mpl_toolkits.mplot3d theta1,theta2=np.mgrid[-500:500:20j,-500:500:20j] J_theta=theta1**2 ax=plt.subplot(111,projection='3d') ax.plot_surface(theta1,theta2,J_theta,rstride=1,cstride=1) ax.set_xlabel('theta1') ax.set_ylabel('theta2') ax.set_zlabel('J_theta') plt.show()
效果如下:

可以发现$J(\theta )=\frac{1}{2}(2000\theta _1+5\theta _2)^{2}$和$J(\theta )=\theta _1^{2}$的图非常相似。
这说明什么呢?在$\theta _1$强大的权值$2000^2$下,后面那一项$25\theta _2^{2}$几乎可以忽略不计了。更确切地说,同样作为可以影响cost函数$J(\theta )$的变量,$\theta _1$拥有着巨大的权值,使得它只须改变一点点,就会引起cost函数的风云巨变;反之,$\theta _2$只拥有一个很小很小的权值25,这使得$\theta _2$再怎样努力变化,也很难使得cost函数受到影响,所谓人微言轻。这也是为什么在第一幅Python示意图中,$25\theta _2^{2}$几乎没有存在感。
我想我应该把这一部分讲得比较清楚了。
2-1-2 特征缩放
(1)什么是特征缩放
正如2-1-1所述,如果直接把特征1的范围0~2000、特征2的范围1~5拿来用,则会出现一条非常非常狭长的椭圆,这一点将对梯度下降法造成困难,使得梯度下降法的路径非常之复杂(四处乱走,正如上面第二幅图那张课件中红线画的那样)。
解决方案很简单,只需要令:
$x_{1}^{(i)}=\frac{size(feet)}{2000}$
$x_{2}^{(i)}=\frac{(number\ of\ bedrooms)}{5}$
即可将$x_{1}^{(i)}$、$x_{2}^{(i)}$皆规整到一个差不多的范围,这样一来梯度下降法就好进行多了。这种方法被称之为“特征缩放”。
(2)特征缩放的目的
目的:让梯度下降法进行得更快。
2-1-3 均值归一化(Mean Normalization)

这个见最下面那个公式就可以了。使用$\frac{x_1-\mu _1}{S_1}$来替换一个待缩放特征$x_1$,其中:
(1)$S_1$为特征的范围(range=max-min),或者标准偏差。目测这里标准偏差才是各种paper和book通用的,不过为了降低难度,Ng说直接使用$S_1=max-min$就可以;
(2)$\mu _1$则是训练样本点$x_1$的*均值,这跟概率论中的表述是一样的。就拿$x_1$的范围为0~2000为例,那么它的*均值$\mu _1$=(0+2000)/1000;而$x_2$的范围为1~5为例,那么它的*均值$\mu _2$=(1+5)/2=3。
(2016.7.4记)
(未完待续)
by 悠望南山



