bzoj4244: 邮戳拉力赛 dp
Description
IOI铁路是由N+2个站点构成的直线线路。这条线路的车站从某一端的车站开始顺次标号为0...N+1。
这条路线上行驶的电车分为上行电车和下行电车两种,上行电车沿编号增大方向行驶,下行电车沿编号减小方向行驶。乘坐这两种电车的话,移动1站的距离需要T秒。换句话说,乘坐上行电车从车站i走到车站i+1需要T秒,称作下行电车从车站i走到车站i-1也需要T秒。你不能在0号车站乘坐下行电车,或在N+1号车站乘坐上行电车。由于电车发车的频率非常高,你可以无视等待电车消耗的时间。
每个车站设有上行电车的站台和下行电车的站台,连接两个站台的道路上设有邮戳台。
现在,IOI铁路召开了邮戳拉力赛。在拉力赛中,选手需要从0号车站的上行电车站台出发,在1...N号车站各盖一枚邮戳,最终到达N+1号车站的上行电车站台即可完成。
为了在每个车站盖上邮戳,必须从电车上下来,步行走到车站通路上的邮戳台。在i号车站的上行电车站台、邮戳台、下行电车站台之间移动所消耗的时间如下所示:
从车站i的上行电车站台到邮戳台的时间为Ui秒
从车站i的邮戳台到上行电车站台的时间为Vi秒
从车站i的下行电车站台到邮戳台的时间为Di秒
从车站i的邮戳台到下行电车站台的时间为Ei秒
邮戳拉力赛的选手只能访问0号车站与N+1号车站各一次。1...N号车站都可以访问任意多次。
现在给出有邮戳台的车站个数、乘坐电车移动一站的时间、在每个车站的上行电车站台、邮戳台、下行电车站台之间移动所消耗的时间,请你求出完成邮戳拉力赛的最短时间。
这个时间包括从0号车站出发,按下N个邮戳后到达N+1号车站的时间。无视等车的时间和按邮戳的时间。
Input
第一行两个空格分隔的整数N和T,表示有N+2个车站,电车行驶一站的距离需要T秒
接下来N行,第i行有四个空格分隔的整数Ui,Vi,Di,Ei,分别表示:
从车站i的上行电车站台到邮戳台的时间为Ui秒
从车站i的邮戳台到上行电车站台的时间为Vi秒
从车站i的下行电车站台到邮戳台的时间为Di秒
从车站i的邮戳台到下行电车站台的时间为Ei秒
Output
输出一行一个整数,表示完成邮戳拉力赛的最短时间。
题解
woc看了整整4个小时题解把自己刚废了,最后终于在神仙yyc的讲解下懂了tql%%%!
首先我们考虑,上行车站到邮戳的距离可能不如下行车站到邮戳更优,于是我们就可能要倒回去转车站。
但一旦我们从上行车站倒到下行车站,就一定要从某个下行车站回到上行车站,否则无法到达终点,故最后从上行车站到下行车站的次数要等于下行车站到上行车站的次数。
然后我们考虑,在\(i\)这个车站,我们可以进行四种操作:
1.从上行车站拿到邮戳回到上行车站,时间为\(u+v\)
2.从下行车站拿到邮戳回到下行车站,时间为\(d+e\)
3.从上行车站转到下行车站(经过邮戳,同下),时间为\(u+e\)
4.从下行车站转到上行车站,时间为\(d+v\)
而3、4的操作会影响上行车站到下行车站的次数和下行车站到上行车站的次数,又因为 下行车站到上行车站的次数 - 上行车站到下行车站的次数 大于等于 0,
我们记\(f[i][j]\)为前\(i\)个邮戳都拿过的情况下,下行车站到上行车站的次数 - 上行车站到下行车站的次数为\(j\)的最短时间(不考虑从\(0\)到\(n+1\)上行的时间)。
为什么要记\(j\)呢?我们考虑由于我们是从下往上递推的,所以这里表示在\(i\)这个车站时有\(j\)次在\(1-i\)中间从下行车站转到上行车站,但还没有从上行车站转到下行车站(即这\(j\)次上转下是在\(i\)上面发生的)为了更好理解,如下图所示:
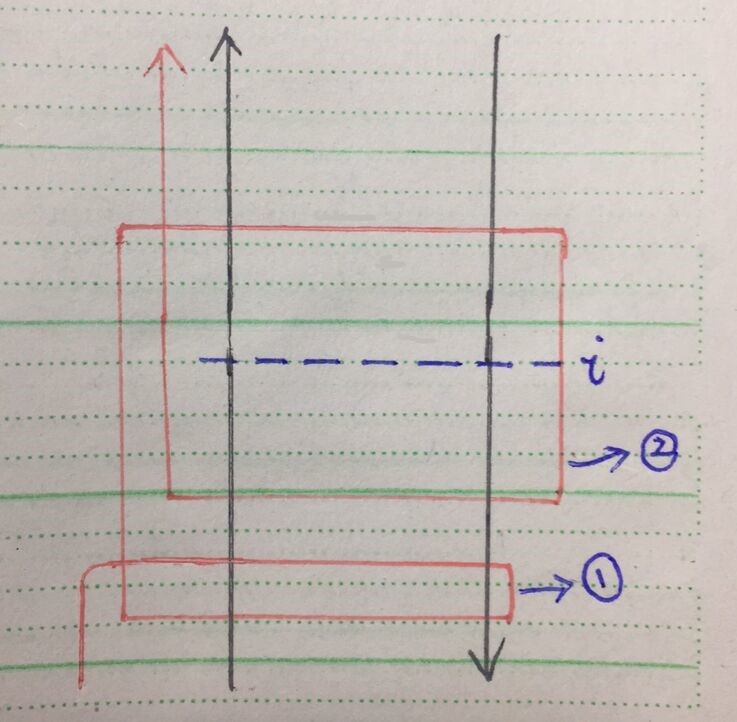
对于第一条边是上转下已在\(i\)以下,已经统计过答案的,是不包含在\(j\)次转弯中的,但第二条边则满足上转下在\(i\)上面,而下转下在\(i\)以下,(观察图可以看出)一定会经过\(i\)这个车站两次,需要给答案加上\(2*T\)。故每次要给\(f[i][j]\)的值要加上\(j*2*T\)。
除此之外,我们考虑如何从\(i-1\)递推到\(i\)。
首先对于1,2不会影响\(j\)值的转移则为
我们之前说过,第3、4的操作会影响\(j\)值。
对于3,若由上行车站转到下行车站,相当于和\(j\)次下转上中的一次转弯联通成一个环,即消掉了一次下转上,则转移为
对于4,若由下行车站转到上行车站,相当于又增加了一次下转上的转弯,则转移为
最后还有两个,是在处理完\(i\)的所有其他情况下,再进行3、4的转弯,即在\(i\)处多次转弯,转移为
最后在加上从\(0\)到\(n+1\)的上行时间,然后就完美解决啦~
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=3000+10;
const int INF=0x3f3f3f3f;
int n,T;
int u,v,d,e;
int f[maxn][maxn];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>T;
memset(f,INF,sizeof(f));
f[0][0]=0;
for(int i=1;i<=n;i++){
cin>>u>>v>>d>>e;
for(int j=1;j<=n;j++)f[i-1][j]+=j*T*2;
for(int j=0;j<n;j++)f[i][j]=min(f[i][j],f[i-1][j+1]+u+e);
for(int j=1;j<=n;j++)f[i][j]=min(f[i][j],f[i-1][j-1]+d+v);
for(int j=1;j<=n;j++)f[i][j]=min(f[i][j],f[i-1][j]+d+e);
for(int j=0;j<=n;j++)f[i][j]=min(f[i][j],f[i-1][j]+u+v);
for(int j=1;j<=n;j++)f[i][j]=min(f[i][j],f[i][j-1]+d+v);
for(int j=n-1;j>=0;j--)f[i][j]=min(f[i][j],f[i][j+1]+u+e);
}
cout<<f[n][0]+(n+1)*T<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号