关于韦神做过的100题中第七题的思考

这道题出自韦神做过的100题。

嗯哼？没思路？

这道题在"100道思考 好 题" 中，自然需要思考的。

什么？暴力枚举？

我一开始的思路也是这样的：把所有的区间画出来，然后慢慢地判断是否符合条件。

什么？还是没想出来？

别急，我思考了30分钟……

算了，来看看解答吧。

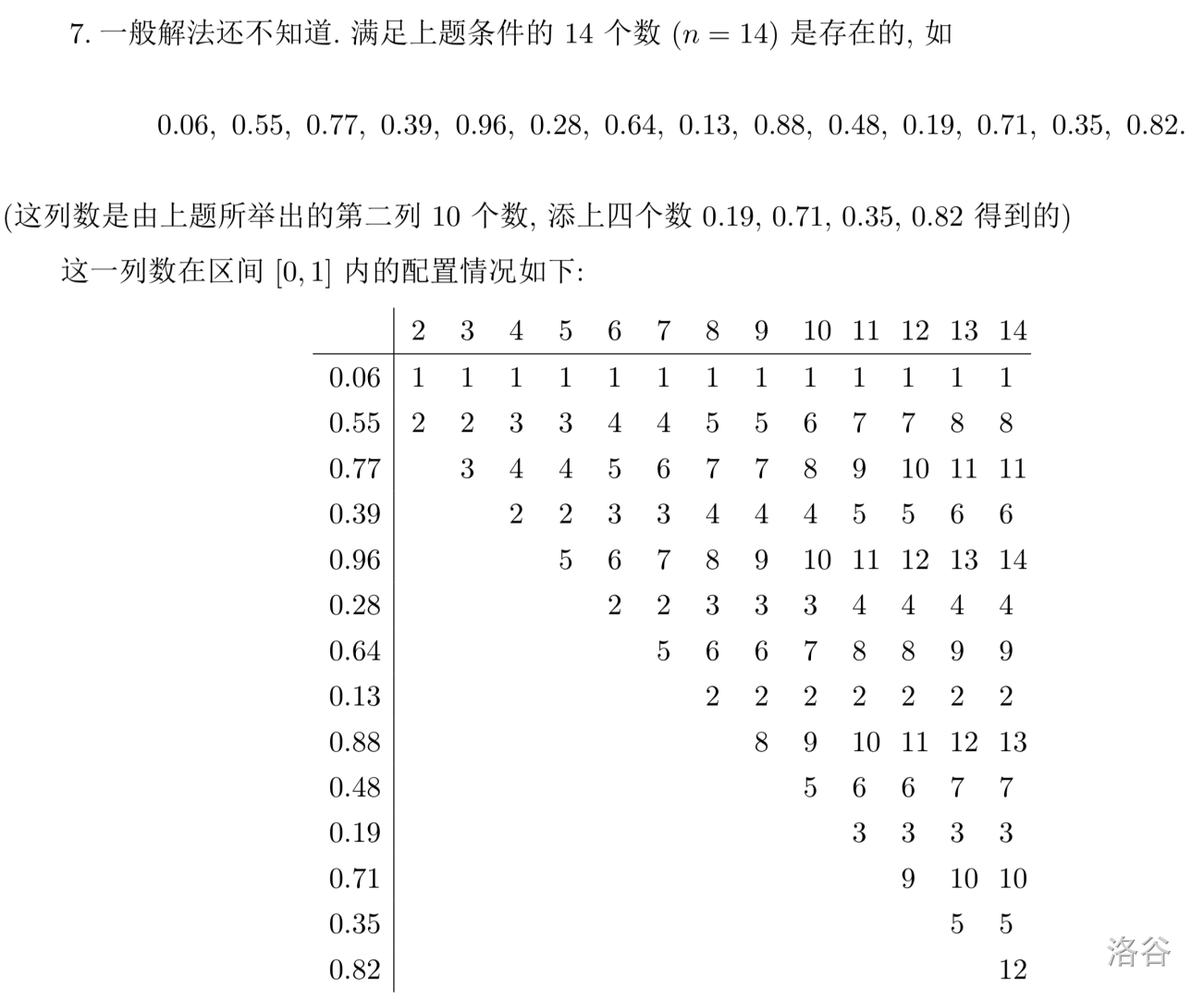
这时，我有一个危不足道的小想法。

可以观察到，\(n=10\) 的时候，有一组解的前两个数比较靠近两个极端（即，一个很靠近 \(0\) 一个很靠近 \(1\)）

不过，这样想后面也是走不通的。

此外，有一个重要的性质：交换前两个数不影响最后结果。

数学的方法似乎走不通了。作为一个连 CSP-S 2021 廊桥分布 都不会做的菜OIer，只会爆搜。

重要声明：比如 \(x_1=0.5\) 之类的，正好是某个 \(i/j\) 且 \(j\le n\) 之类的情况我不考虑，因为这没什么意义。你可以加一个小量或者减去一个小量来让它分进一个区间内。

思路

当然，也不能盲目地把每一个小数都搜一遍。

我这时有了一个思路：

考虑 \(n=10\)，那么 \(0.0000000114514\) 和 \(0.00000001919810\) 是没有本质区别的，因为它们都落在 \(0\sim 0.1\) 这个区间里。

所以，如果两个数对于所有 \(1\le i\le n\)，都落在某个 \(\dfrac{k}{i}\sim \dfrac{k+1}{i}\) 的范围内，那么这两个数就是等价的。

因此，我的最终思路就是：对于 \(1\le j\le i\le n\)，用所有的 \(\frac{j}{i}\) 把 \((0,1)\) 分割成若干个区间。在每个区间里选一个代表（我选的是区间的中点），然后搜索 \(x_1\sim x_n\) 分别代表什么。

朴素的搞一遍，复杂度大概是 \(\Theta(P_m^n)\)，其中 \(m\) 是区间的个数。

这样妥妥的一秒跑不完，一小时甚至也很难。

接下来，就是不停地剪枝优化了。

剪枝

V1

前面提到的一个性质。

我们可以不妨设第一个数 \(<0.5\) ，第二个数 \(>0.5\)。

这样，常数就减到了原来的一半。

V2

另一个很明显的剪枝是，在枚举下一个数之前，先找到下一个数的所有可能值。

这样可以避免在搜到叶子结点的时候，发现靠近根的地方出问题了。

V2.1

这不能算是真正的剪枝。

在找到所有可能可行的方案后，random_shuffle 一下，随机顺序遍历。

时间复杂度

记用分母 \(\le n\) 的真分数可以把 \((0,1)\) 隔成 \(m\) 个区间。

前两个数，各需要 \(m/2\) 次枚举。

搜索到第 \(k\) 层时，假如有解，可能的范围差不多是 \((0,1)\) 区间内的 \(\frac{1}{k}\)，所以差不多有 \(m/k\) 个可能的值继续枚举。

最后，在判断是否合法的时候大概是 \(n\) 左右。（事实上，在已知 \(n=k\) 寻找 \(n=k+1\) 的时候差不多判断 \(k\) 次）

整体来说是 \(\Theta(\dfrac{m^{n-2}}{(n-1)!\times 2})\)

接下来求 \(m\)。

其实，要求这些分数把区间划成几份，就等于 \((0,1]\) 里有多少个分母 \(\le n\) 的不同大小的分数。

令 \(m_k\) 表示 \(n=k\) 时 \(m\) 的值。

\(m_{k+1}\) 时，增加了所有分母是 \(k+1\) 且分子与 \(k+1\) 互质的真分数。

也就是说，增加了 \(\varphi(k+1)\) 个。

因此，\(m_{n}=m_{n-1}+\varphi(n)\) 其中 \(m_1=1\)

所以，\(m_{n}=\sum\limits_{i=1}^{n}\varphi(i)\)

然而，这个时间复杂度远远跑不满。

举个例子：当 \(x_1\in (1/3,1/2),x_2\in (1/2,2/3)\) 时，显然是不行的。

这样的解大概占了全部可能解的 \(\frac{1}{9}\)，所以常数至多 \(\frac{8}{9}\)。

具体的，当 \(n=16\) 时 \(m=80\), \(n=17\) 时 \(m=96\), \(n=18\) 时 \(m=102\).

实际上，我找到 \(n=17\) 的解仅花了5分钟。

算一下，将 \(n=17,m=96\) 代入求时间复杂度的式子，结果是……

\[1.1515\times 10^{16} \]

当然，其实远远达不到这个上界。

按照每秒钟运行 \(2\times 10^8\) 次算，我也只运行了 \(6\times 10^{10}\) 次，还不到使万分之一。

按照这个思路，我决定试试 \(n=18\)。

然而，我运行了好几个小时还没出来结果。

这时，我想到一个新的剪枝。

V3

受到 IDA* 思想的启发

我们只要找 \(n=18\) 的解。所以在判断的时候，我们额外多判断一个：当前选的这些数是否同时满足 \(2\sim 18\) 的条件？

这样，虽然看上去时间复杂度多了一个 \(n\)，但大大减少了不必要的搜索。

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define ll long long

const int N=105;
int n=102;
const double hh[155]={1.0,0.944444,0.941176,0.937500,0.933333,0.928571,0.923077,0.916667,0.909091,0.900000,0.888889,0.882353,0.875000,0.866667,0.857143,0.846154,0.833333,0.823529,0.818182,0.812500,0.800000,0.785714,0.777778,0.769231,0.764706,0.750000,0.733333,0.727273,0.722222,0.714286,0.705882,0.700000,0.692308,0.687500,0.666667,0.647059,0.642857,0.636364,0.625000,0.615385,0.611111,0.600000,0.588235,0.583333,0.571429,0.562500,0.555556,0.545455,0.538462,0.533333,0.529412,0.500000,0.470588,0.466667,0.461538,0.454545,0.444444,0.437500,0.428571,0.416667,0.411765,0.400000,0.388889,0.384615,0.375000,0.363636,0.357143,0.352941,0.333333,0.312500,0.307692,0.300000,0.294118,0.285714,0.277778,0.272727,0.266667,0.250000,0.235294,0.230769,0.222222,0.214286,0.200000,0.187500,0.181818,0.176471,0.166667,0.153846,0.142857,0.133333,0.125000,0.117647,0.111111,0.100000,0.090909,0.083333,0.076923,0.071429,0.066667,0.062500,0.058824,0.055556};
const double pos[105]={1.0,0.972222,0.942810,0.939338,0.935416,0.930952,0.925824,0.919872,0.912879,0.904546,0.894445,0.885621,0.878677,0.870834,0.861905,0.851649,0.839743,0.828431,0.820855,0.815341,0.806250,0.792857,0.781746,0.773505,0.766968,0.757353,0.741667,0.730303,0.724747,0.718254,0.710084,0.702941,0.696154,0.689904,0.677083,0.656863,0.644958,0.639611,0.630682,0.620192,0.613248,0.605555,0.594117,0.585784,0.577381,0.566964,0.559028,0.550506,0.541959,0.535897,0.531373,0.514706,0.485294,0.468627,0.464102,0.458041,0.449495,0.440972,0.433036,0.422619,0.414216,0.405883,0.394444,0.386752,0.379807,0.369318,0.360390,0.355042,0.343137,0.322916,0.310096,0.303846,0.297059,0.289916,0.281746,0.275253,0.269697,0.258333,0.242647,0.233032,0.226496,0.218254,0.207143,0.193750,0.184659,0.179144,0.171569,0.160257,0.148352,0.138095,0.129167,0.121324,0.114379,0.105555,0.095454,0.087121,0.080128,0.074176,0.069048,0.064584,0.060662,0.057190,0.027778};
int a[N],vis[N][N],ava[N][N],cnt[N];
bool viss[N]; 
ll CNT=0;
FILE *FI;
int QAQ=0;
int tt[3005];
char name[505];
int ccnntt[25];
int qwq1,qwq2; 
void dfs(int dep)
{
	if(dep==0)
	{
		for(int i=1;i<=51;i++) ava[1][i]=i;
		for(int i=1;i<=51;i++) ava[2][i]=i+51;
		cnt[1]=51;
		cnt[2]=51;
		for(int i=1;i<=51;i++)
		{
			if(i<qwq1) continue;
			for(int j=1;j<=51;j++)
			{
				if(i==qwq1&&j<qwq2) continue;
				a[1]=i;
				a[2]=j+51;
				memset(viss,0,sizeof(viss));
				dfs(2);
			}
		}
		viss[1]=viss[2]=1;
		return;
	}
	if(dep==2) 
	{
		printf("------[1]%d [2]%d-------\n",a[1],a[2]-51); 
		FI=fopen("record.txt","w");
		fprintf(FI,"%d %d %d %d",a[1],a[2]-51,ccnntt[17],ccnntt[18]);
		fclose(FI);
	} 
	if(dep>=18||!viss[dep])
	{
		viss[dep]=1;
		printf("dep=%d: ",dep);
		for(int i=1;i<=dep;i++) 
		{
			printf("%lf ",pos[a[i]]);
	//		vis[dep][i]=0;
		}	
		printf("\n");
		
		if(dep>=17)
		{
			sprintf(name,"a%d-%d.txt",dep,++ccnntt[dep]);
			FI=fopen(name,"w");
			for(int i=1;i<=dep;i++) fprintf(FI,"%lf ",pos[a[i]]);
			fclose(FI);
	memset(vis,0,sizeof(vis)); 
	for(int j=dep+1;j<=17;j++)
	{
		for(int i=1;i<=dep;i++)
		{
			if(vis[j+1][(int)ceil(pos[a[i]]*(double)(j+1))]) return; 
			vis[j+1][(int)ceil(pos[a[i]]*(double)(j+1))]=1;
		}	
	}
	for(int i=1;i<=dep;i++)
	{
		if(vis[dep+1][(int)ceil(pos[a[i]]*(double)(dep+1))]) return; 
		vis[dep+1][(int)ceil(pos[a[i]]*(double)(dep+1))]=1;
	}
	cnt[dep+1]=0;
	for(int i=1;i<=102;i++)
	{
		if(!vis[dep+1][(int)ceil(pos[i]*(double)(dep+1))]) 
		{
			ava[dep+1][++cnt[dep+1]]=i;
		}
	}
	random_shuffle(ava[dep+1]+1,ava[dep+1]+cnt[dep+1]+1);
	int qwq=cnt[dep+1];
	for(int i=1;i<=qwq;i++)
	{
		
		a[dep+1]=ava[dep+1][i];
		dfs(dep+1);
	}
	
} 
int main()
{
	srand(time(0));
	memset(viss,0,sizeof(viss));
	memset(ccnntt,0,sizeof(ccnntt));
	FI=fopen("record.txt","r");

	fscanf(FI,"%d%d%d%d",&qwq1,&qwq2,&ccnntt[17],&ccnntt[18]);
	fclose(FI);	
	dfs(0);
	return 0;
}

最后只用了五个小时就搜索完了全部的可能情况！

让我震惊的是，似乎没有 \(n=18\) 的解！

目前正在想数学方法证明。

最终结果

经过多方认证，确实不存在 \(n=18\) 的解，但均为计算机认证。