【洛谷11月月赛】赛后解题报告

题面

请戳这儿~~

T1

这个题第一眼看到觉得是巨大的斐波拉契的降级版

但是定睛一看发现说要推到m²，才能保证没有重复，心想只能得70的暴力

然后其实就过了。正确姿势是可以只保留三个数滚动递推的。

后来看了其他人的题解，为什么能过呢？

因为打表发现ans和m的倍数关系不超过7倍...

upd:来自出题人的评讲

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll M=10000000;
ll f[M];
ll m,ans;
int main()
{
    cin>>m;f[0]=0,f[1]=1;
    for(ll i=2;i<M;i++)
    {
        f[i]=(f[i-1]+f[i-2])%m;
        if(f[i]==1&&f[i-1]==0)
        {
            ans=i-1;
            break;
        }
    }    
    cout<<ans;
}

T2

很简单的贪心，但是洛谷上的题解也很少有人证明，其实证明也很简单，就是微扰法（邻项互换法）

降序排序后得到a₁ a₂...a_n

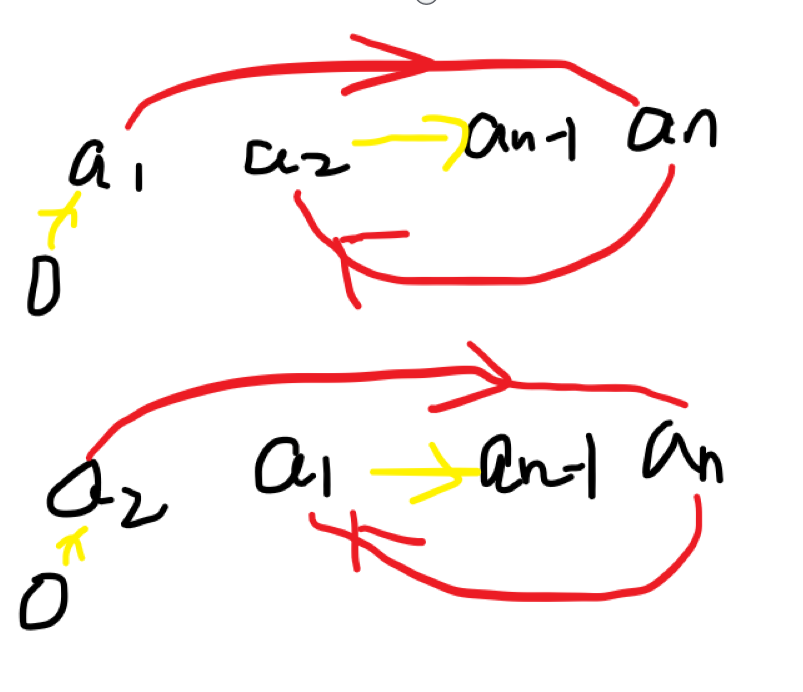
上面是最优的跳法，即选择离现在高度差最大的点跳

交换第一项第二项后，红线加起来是相同的价值，而黄线是不同的，因此只计算黄线的差异（首先从0跳到最大值点）。

上面的答案是a₁²+（a₂-a_n-1）²，下面的答案是a₂²+(a₁-a_n-1)²

全部展开，可得到第一个是a₁² +a₂²-2a₂a_n-1+a_n-1²，第二个是a₂²+a₁²-2a₁a_n-1+a_n-1²

平方项相加是相同的，不同的是-2a₂a_n-1和-2a₁a_n-1，因为a₂<a₁，所以前式<后式，减得更少，答案也就更大了。

因此交换计算顺序后一定不划算。

代码

#include<bits/stdc++.h>
using namespace std;
#define N 303
#define ll long long
ll n,ans,tmp;
ll a[N];
int main()
{
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++)scanf("%lld",&a[i]);
    a[n+1]=0;n++; 
    sort(a+1,a+n+1);
    for(ll i=1;i<=(n>>1);i++)
        ans+=(a[n-i+1]-a[i])*(a[n-i+1]-a[i])+(a[n-i+1]-a[i+1])*(a[n-i+1]-a[i+1]);    
    printf("%lld\n",ans);
    return 0;
}

T3

这里

T4

待填坑

太困难了

被我咕咕咕掉