【BZOJ4811】睡觉困难综合征
题面
给你一个有n个点的树,每个点的包括一个位运算opt和一个权值x,位运算有&,l,^三种,分别用1,2,3表示。每次询问包含三个数x,y,z,初始选定一个数v。然后v依次经过从x到y的所有节点,每经过一个点i,v就变成v optixi,所以他想问你,最后到y时,希望得到的值尽可能大,求最大值?给定的初始值v必须是在[0,z]之间。每次修改包含三个数x,y,z,意思是把x点的操作修改为y,数值改为z。
0 <= n , m <= 100000 , k <= 64
分析
应该先做起床困难综合征!!!
同理我们用p0和p1来表示全0和全1经过这个点过后的值。刚好unsigned long long就能开下。
考虑线段树上这么合并呢??
形象一点儿,合并其实就是再走过这一段。只不过从左往右走和从右往左走不同,要分别维护。
ans.p0=l.p0&r.p1 or (~l.p0&r.p0) 0出发的点的穿过l变成1再穿过r的结果 或者0出发的点穿过l变成0再穿过r的结果
1也同理,然后记得反着来一遍(先穿r再穿l)
然后坑点就是unsigned long long,最后那个类似起床困难综合征的贪心求答案的时候1一定要强制转成ull
代码
- #include<bits/stdc++.h>
- using namespace std;
- #define N 100010
- #define lc (p<<1)
- #define rc (p<<1|1)
- #define mid (t[p].l+t[p].r>>1)
- #define ull unsigned long long
- int n,m,k,P,idx,cnt;
- int d[N],f[N],id[N],rk[N],top[N],siz[N],son[N],first[N];
- ull op[N][2];
- struct email
- {
- int u,v;
- int nxt;
- }e[N*4];
- struct tree
- {
- int l,r;
- }t[N*4];
- struct px
- {
- ull p1,p0;
- }tl[N*4],tr[N*4];
- template<class T>
- void read(T &x)
- {
- x = 0;
- static char c = getchar();
- while(c < '0' || c > '9') c = getchar();
- while(c >= '0' && c <= '9')
- x = x * 10 + c - '0', c = getchar();
- }
- inline px pushup(px l, px r)
- {
- px ret;
- ret.p0=(l.p0&r.p1)|((~l.p0)&r.p0);
- ret.p1=(l.p1&r.p1)|((~l.p1)&r.p0);
- return ret;
- }
- inline px change(ull op,ull w)
- {
- px ans;
- if(op==1)ans.p0=0&w,ans.p1=(-1)&w;
- if(op==2)ans.p0=0|w,ans.p1=(-1)|w;
- if(op==3)ans.p0=0^w,ans.p1=(-1)^w;
- return ans;
- }
- inline void build(int p,int l,int r)
- {
- t[p].l=l,t[p].r=r;
- if(l==r)
- {
- tl[p]=tr[p]=change(op[rk[l]][0],op[rk[l]][1]);
- return ;
- }
- int bm=l+r>>1;
- build(lc,l,bm);build(rc,bm+1,r);
- tl[p]=pushup(tl[lc],tl[rc]);tr[p]=pushup(tr[rc],tr[lc]);
- }
- inline void update(int p,int x,ull op,ull w)
- {
- if(t[p].l==t[p].r){tl[p]=tr[p]=change(op,w);return;}
- if(x<=mid)update(lc,x,op,w);
- else update(rc,x,op,w);
- tl[p]=pushup(tl[lc],tl[rc]);tr[p]=pushup(tr[rc],tr[lc]);
- }
- px query(int p,int ql,int qr,int fg)
- {
- if (ql<=t[p].l&&qr>=t[p].r)
- if (fg) return tr[p];
- else return tl[p];
- if (qr<=mid) return query(lc,ql,qr,fg);
- else if (ql>mid) return query(rc,ql,qr,fg);
- else return pushup(query(lc+fg,ql,qr,fg),query(rc-fg,ql,qr,fg));
- }
- inline void add(int u,int v)
- {
- e[++cnt].nxt=first[u];first[u]=cnt;
- e[cnt].u=u;e[cnt].v=v;
- }
- inline void dfs1(int u,int fa,int dep)
- {
- siz[u]=1;f[u]=fa;d[u]=dep;
- for(int i=first[u];i;i=e[i].nxt)
- {
- int v=e[i].v;
- if(v==fa)continue;
- dfs1(v,u,dep+1);
- siz[u]+=siz[v];
- if(siz[v]>siz[son[u]]||son[u]==0)
- son[u]=v;
- }
- }
- inline void dfs2(int u,int t)
- {
- top[u]=t;id[u]=++idx;rk[idx]=u;
- if(son[u]==0)return ;
- dfs2(son[u],t);
- for(int i=first[u];i;i=e[i].nxt)
- {
- int v=e[i].v;
- if(v!=f[u]&&v!=son[u])
- dfs2(v,v);
- }
- }
- px asktree(int x,int y)
- {
- int fx=top[x],fy=top[y];
- px ans1=change(3,0),ans2=change(3,0);
- while(fx!=fy)
- {
- if(d[fx]>=d[fy])
- {
- ans1=pushup(ans1,query(1,id[fx],id[x],1));
- x=f[fx];fx=top[x];
- }
- else
- {
- ans2=pushup(query(1,id[fy],id[y],0),ans2);
- y=f[fy];fy=top[y];
- }
- }
- if(d[x]>=d[y])
- return pushup(pushup(ans1,query(1,id[y],id[x],1)),ans2);
- else
- return pushup(pushup(ans1,query(1,id[x],id[y],0)),ans2);
- }
- void find(int x,int y,ull z)
- {
- px ans=asktree(x,y);ull state=0,ret=0;
- for(int i=P;i;i--)
- if(ans.p0&((ull)1<<i-1))ret+=(ull)1<<i-1;
- else if((ans.p1&((ull)1<<i-1)&&((ull)1<<i-1)+state<=z))
- ret+=(ull)1<<i-1,state+=(ull)1<<i-1;
- printf("%llu\n",ret);
- }
- int main()
- {
- read(n);read(m);read(P);
- for(int i=1;i<=n;i++)read(op[i][0]),read(op[i][1]);
- for(int i=1;i<n;i++)
- {
- int u,v;
- read(u),read(v);
- add(u,v);add(v,u);
- }
- dfs1(1,1,1);dfs2(1,1);build(1,1,n);
- while(m--)
- {
- int flag,x,y;ull z;
- read(flag);read(x);read(y);read(z);
- if(flag==2)update(1,id[x],y,z);
- else find(x,y,z);
- }
- return 0;
- }
闲聊
此题调的时候出锅了,炸了一次
然后在debug下发现是query炸了 从头到尾看了query好几遍也不知道为啥炸了 好了重构了 query
重构了就没炸了 2333 所以有闲心的朋友可以找找不同 是哪里炸了TAT 反正最后看出来了。。其实很明显 【可能我瞎
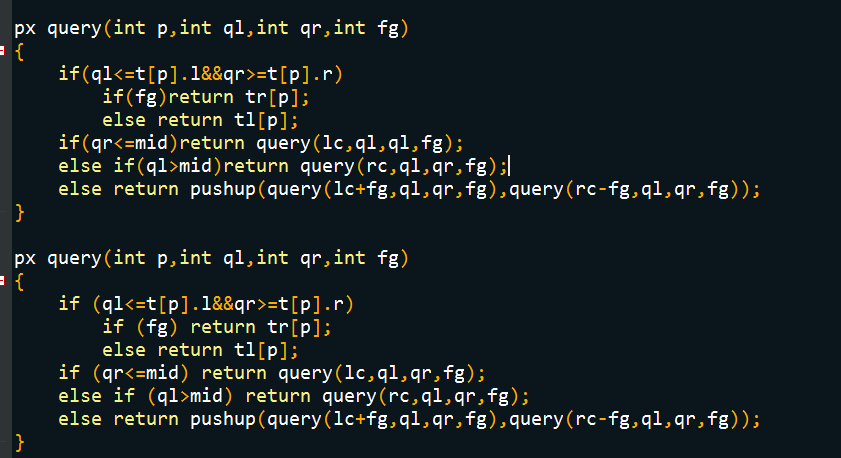
还有我强调那个unsinged long long 是因为被教做人了
有一组数据
答案是 18446744073709551615 然而我输出的 18446744073709551614
唉TAT
调这题单循T T 这首歌【没错颜文字歌名
放了27次。。还好调了不是太久 27*3.5=94.5 min

感谢收看我的闲聊(fei hua)
“Make my parents proud,and impress the girl I like.”


 浙公网安备 33010602011771号
浙公网安备 33010602011771号