【暑期实训】Week2
这一周比前一周的节奏更为固定吧,前一周就无脑刷题,一溜烟地扑在题上,这周因为能做的题基本上都做完了,老师一般只会提前一天给题,所以一般就是早上写一下第二天的题,下午晚上自学一下计组的网课,然后有时帮同学debug,基本上就是三点一线的生活。
这一周老师上课的内容流程是:树和图,dfs,bfs,搜索进阶,最短路和次短路,启发式搜索
基本上算是一点图论+暴搜教学。其实还是比较实用的,搜索能解决的问题实在是太多了,练好搜索真的非常有用。但是我个人感觉像图论给的那几个最短路过于模板了,一点脑子都不用转,而启发式搜索给的两道例题都不太经典。
一道是状压dp的裸板,不过我确实没想到A*怎么搜,用状压写过后看了一下网站给的题解,是贪心出最大值然后用来剪枝。我寻思,这是A而不是A*吧,A*的h(x)是不能比实际值大的才对。
第二题我也不知道怎么个A*法,就暴搜+剪枝,然后也过了,当然数据范围太小,打表也能过。总而言之这两题实在不适合拿来练启发式搜索,个人觉得k短路或者八数码这种典型一点的比较适合。
下面也是选一些题写一下简要的题解。
引爆炸弹
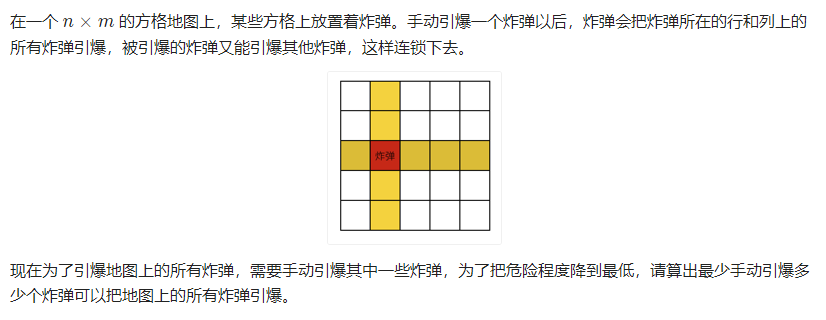

一句话题解:这题就是个染色问题,把一个炸弹所在行和列的炸弹全部染色,再dfs这些炸弹即可
#include<stdio.h> #include<string.h> #define N 660 int n,m,temp,tot,num; int a[N][N]; int xx[5]={0,0,0,1,-1}; int yy[5]={0,1,-1,0,0}; void dfs(int x,int y) { a[x][y]=0; temp++; for(int i=x+1;i<=n;i++) if(a[i][y]) dfs(i,y); for(int i=x-1;i>=0;i--) if(a[i][y]) dfs(i,y); for(int j=y+1;j<=m;j++) if(a[x][j]) dfs(x,j); for(int j=y-1;j>=0;j--) if(a[x][j]) dfs(x,j); } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { char s[N]; scanf("%s",s); for(int j=1;j<=m;j++) { if(s[j-1]=='1') { a[i][j]=1; tot++; } } } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { if(a[i][j]) { temp=0; dfs(i,j); tot-=temp; num++; if(tot==0) break; } } printf("%d",num); }
次短路
次短路的思路大概分为两种,一种是在更新最短路的同时更新次短路,一种是求出最短路后,枚举更换一条边找到次短路;
第一种做法,同时更新
d1[u]+w<d1[v] =>d1[v]=d1[u]+w
d2[v]+w>max(d1[u]+w,d1[v]) && d1[v]<max(d1[u]+w,d1[v]) =>d2[v]=max(d1[u]+w,d1[v])
第二种做法,删边法
正反各一次最短路求出d1[i]和dn[i]
在枚举边,求出d1[u]+w+dn[v]小于最短路的最大值。
蒜头君分玩具


这个数据范围以及状态数量很多但是选择很单一的情况,非常符合状压dp的特征
对于每个玩具的状态压成一个二进制数存入dp[i][j]中
dp[i][j]表示做到前i个小朋友时,状态为j的最大值
可知转移方程 dp[i][j|(1<<k)]=max(dp[i][j|(1<<k)],dp[i-1][j]+a[i][k]
即取这个玩具或不取这个玩具
#include<stdio.h> #define N 20 int n; int a[N][N],dp[N][1<<N]; int max(int a,int b){return a>b?a:b;} int main() { scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&a[i][j]); for(int i=1;i<=n;i++) for(int j=0;j<(1<<n);j++) for(int k=0;k<n;k++) if(!(j&(1<<k))) dp[i][j|(1<<k)]=max(dp[i][j|(1<<k)],dp[i-1][j]+a[i][k+1]); printf("%d\n",dp[n][(1<<n)-1]); }
Besty的旅行
dfs+剪枝
剪枝的方案两种
(1) 如果它上下访问了左右没访问或者左右访问了上下没访问,可以知道它一定被包起来了,出不去了,剪掉。
(2)如果一个格子的周围三个格子都被访问了,那就必须走这个格子,如果现在不走以后肯定是死路,如果同时出现两个这样的格子,这种情况就无解了,剪掉。
#include<stdio.h> #include<string.h> #define N 10 int n,ans=0; int xx[5]={0,0,0,1,-1}; int yy[5]={0,1,-1,0,0}; int vis[N][N]; int check1(int x,int y) { if(x==n&&y==1)return 0; int ok=0; if(vis[x-1][y]&&vis[x+1][y]&&!vis[x][y-1]&&!vis[x][y+1]) ok=1; if(!vis[x-1][y]&&!vis[x+1][y]&&vis[x][y-1]&&vis[x][y+1]) ok=1; return ok; } int check2(int x,int y) { if(x==n&&y==1)return 0; int tmp=0,ok=0; for(int i=1;i<=4;i++) { int dx=x+xx[i],dy=y+yy[i]; if(vis[dx][dy]) tmp++; } if(tmp==3) ok=1; return ok; } void dfs(int x,int y,int d) { if(x==n&&y==1) { if(d==n*n-1) ans++; return ; } if(d==n*n-1)return ; vis[x][y]=1; int cnt=0,cot=0; int tx[N*N],ty[N*N],lax[N*N],lay[N*N]; for(int i=1;i<=4;i++) { int dx=x+xx[i],dy=y+yy[i]; if(dx>n||dx<1||dy>n||dy<1)continue; if(vis[dx][dy])continue; if(check1(dx,dy))continue; if(check2(dx,dy)) { tx[++cnt]=dx; ty[cnt]=dy; } else { lax[++cot]=dx; lay[cot]=dy; } } if(cnt>1) { vis[x][y]=0; return ; } if(cnt==1) { int dx=tx[1],dy=ty[1]; dfs(dx,dy,d+1); } else { for(int i=1;i<=cot;i++) { int dx=lax[i],dy=lay[i]; dfs(dx,dy,d+1); } } vis[x][y]=0; } int main() { scanf("%d",&n); for(int i=0;i<=n+1;i++) { vis[0][i]=1; vis[i][0]=1; vis[n+1][i]=1; vis[i][n+1]=1; } vis[1][1]=1; dfs(1,1,0); printf("%d\n",ans); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号