XIN队算法

骗分导论

已同步到 \(cnblog\) 中

\(newly\;upd:2021.10.18\)

\(newly\;upd:2021.8.4\)

\(newly\;upd:2021.8.1\)

\(newly\;upd:2021.7.8\)

\(newly\;upd:2021.6.6\)

OI至高算法，只要XIN队算法打满，保证所有比赛 \(rk1\)，碾爆标程，让对手望尘莫及。

请慎用

注：名称由莫队算法改编而来

XIN队算法：

1.遇到不会做的题目不用慌，你要想到你还有XIN队算法，仔细读题，理解题目意义，然后开始准备写XIN队算法。

2.这时候，你可以潇洒地敲出：

void xin_team()

然后开始暴搜

XIN队算法框架：

    void xin_team(参数)
    {
        if(边界) return;
        for(register int i=1;i<=n;++i)
            if(条件1)
            {
                状态转移
                xin_team(参数);
                状态回溯
            }
    }

但是，对于不同的题目, void xin_team 并不能解决所有的题目，那该怎么办呢？？？

对于很多不能用XIN队\(1\)号算法的，大多数可以使用XIN队\(2\)号算法：
next_permutation(a+1,a+n+1); 大法

框架：


    void xin_team2
    {
        do
        {
            答案记录
        }while(next_permutation(a+1,a+n+1));
    }

非常完美

但是，由于XIN队算法时间复杂度只有 \(\mathcal O(2^n)\)或者是\(\mathcal O(n!)\)，所以我们提出优化：

优化XIN队算法：

非常不建议使用

框架：

        srand((unsigned)time(0));
        do
        {
            random_shuffle(a+1,a+n+1);
            答案记录
        }while(next_permutation(a+1,a+n+1));

复杂度:

\[\huge{\mathcal O(\lim_{time\to\infty})} \]

还附加超大常数

XIN队算法升级：二维XIN队

有很多很多的题目无法用普通的\(XIN\)队算法解决，这时候我们就需要\(XIN\)队算法升级版：\(\color{red}\huge_{\text{二维XIN队}}\)

二维\(XIN\)队对于代码能力的提升是显而易见的，~~然而对复杂度的提升更是显而易见的~~，二维\(XIN\)队算法框架：

比方说：

[SDOI2015]排序

使用此算法，轻松 \(30pts\)

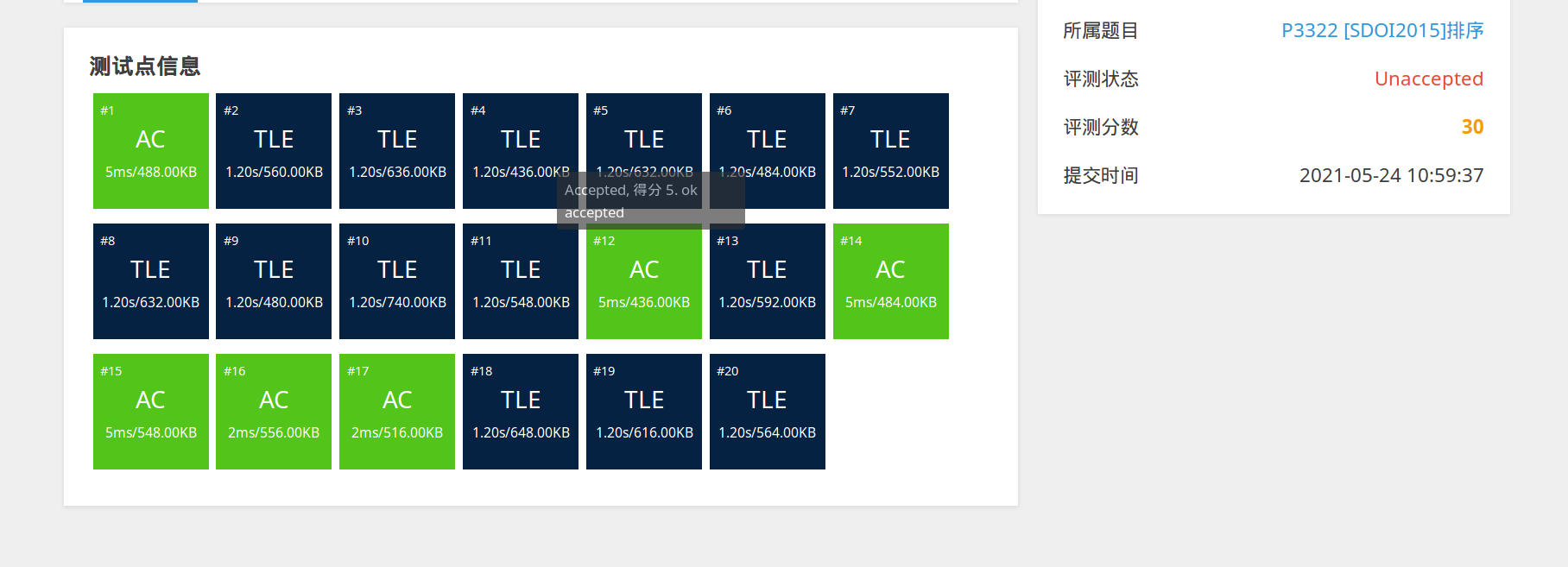
	void xin_team2(int x,int now)
	{
		if(边界) 
		{
			xin_team2(x,now);
			记录
			return ;
		}
		for(register int i=1;i<=n;++i)
		{
			记录状态
			xin_team(x,now+1);
			回溯状态
		}
	}
	void xin_team1(int x,int now)
	{
		if(边界) 
		{
			xin_team2(x,now);
			记录
			return ;
		}
		for(register int i=1;i<=n;++i)
		{
			记录状态
			xin_team(x,now+1);
			回溯状态
		}
	}

复杂度：

\[\huge{\mathcal O(n! * 2^n)} \]

~~并且只能说是大概~~

我们发现，对于一般的题目，大多是 \(dp\) 解决，然而纯粹运用上述方法只能拿到部分分数，甚至全部 \(TLE\) 所以，记忆化 \(XIN\) 队算法应运而生。

对于优秀的记忆化 \(XIN\) 算法，想要什么状态就去找什么状态，然后就可以实现飞一般的提升。。。

包准快

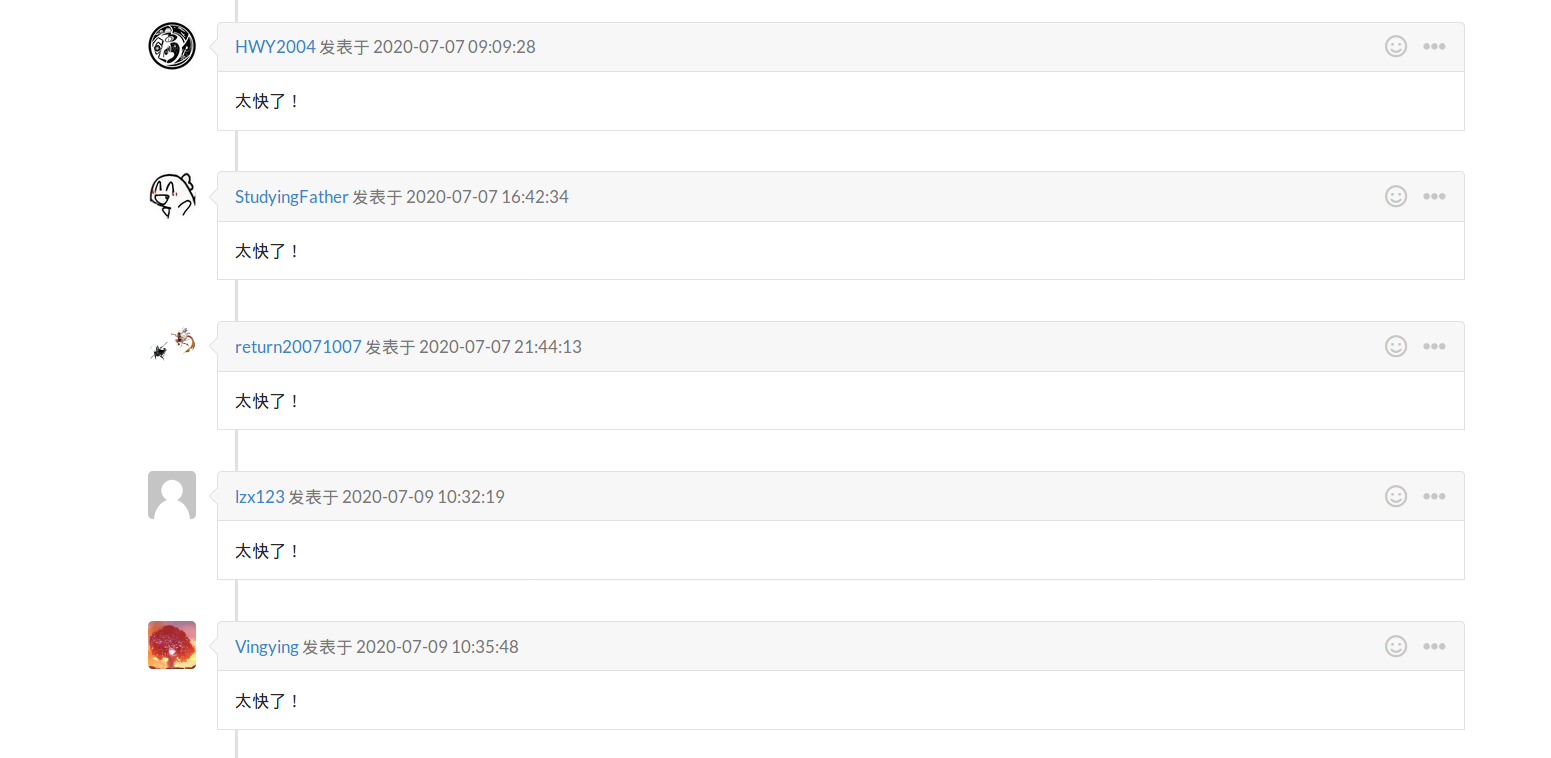
使用记忆化 \(XIN\) 队算法，\(NOI\)包准不打铁！

比方说这个题： \(NOI2020\)美食家

使用 \(XIN\) 队算法，轻轻松松 \(40pts\)

框架：

	void xin_team(int i,int j)
	{
		if(f[i][j]) return f[i][j];
		for(k ...)
			xin_team(k,~);
		return f[i][j];
	}

算法的时间复杂度就是:

\[\huge{\mathcal O (\prod_{i=1}^{n} state_{num_i})} \]

\(num\)为状态，复杂度总体海星。。。

然而：

\(\color{red} \huge{\text{方程推不出}}\)

\(\color{green} \huge{\text{亲人两行泪}}\)

\(XIN\) 优化分块预处理

~~一个月没更了，这次在刷题的时候发现了最新的 \(XIN\) 队算法应用~~

这是在写蒲公英的时候发现的。

做了好长时间，中途还跑去做树链去了。

时间相差的确实长了一些。。。

在用分块解决这个问题的时候。

发现狂 \(T\) 不止。

但是。

~~不知道为什么在其他的 \(OJ\) 上都可以过掉~~

只不过就是很慢。

但是在学校的 \(OJ\) 上最多只有 \(70pts\)。

~~好评测机~~

~~然而并不敢找老师去开大时限~~

所以我只能~~优化暴力~~。。。

然后。

我发现在预处理 \(p_{i,j}\) 的时候，时间差的很多很多。

然而如果用 \(query\) 函数而不是暴力去搞就会错。。。

因为有些需要的状态还没有附上值但是接下来处理需要用到。。。

所以我~~集中生智~~

发现了 \(XIN\) 队优化分块预处理法

~~我都没想到 \(XIN\) 队算法还有优化别的东西的一天~~

主要思想就是 缺啥找啥

然后状态就有了。。。

双指针突然不香了 \(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) --摇摆兵

然后飞快

	void xin_team(int x,int y)
	{
		if(p[x][y]) return;
		if(abs(y - x) <= 2) {p[y][x] = p[x][y] = query(l[x],r[y],0); return;}
		xin_team(x+1,y-1);
		p[x][y] = p[y][x] = query(l[x],r[y],0);
	}

\(\color{red}{\huge{\uparrow \text{精华}}}\)

\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\huge{record}\)

鉴于有童鞋想要学习 clock() 骗分优化方法，那就更新一下下

对于 \(clock()\) 函数的使用，其实还是非常简单的。

\(clock()\) 函数的返回值与 \(time(0)\) 有所不同，\(clock()\) 函数的返回值是从程序开始到你所调用 clock 函数的时间。 然而 \(time(0)\) 的返回值是 从历史上的某一天开始的。所以这两个函数的用法就有所不同。

clock() 直接使用就行
time(0)函数需要在程序开始的时候执行一次，之后在需要的时候再进行调用，之后作差就是程序运行时间。

但是， \(clock()\) 函数的返回值的单位并不是秒，所以我们需要将其进行处理。

CLOCKS_PER_SEC 是 \(C++\) 中的一个常数，在 \(Linux\) 系统下是 \(10^6\)，将 clock() / CLOCKS_PER_SEC 这样处理就是以秒为单位了。

所以我们来一个判断函数：

inline bool pan(){return ((double)clock() > 0.9 * CLOCKS_PER_SEC) ? false : true;}

然后就 \(okk\) 了。

打表骗分方法

关于打表的高级方法，一定要配合 \(XIN\) 队算法使用。

但是如果机子不行。。。。。

就会。。。。

但是没有什么关系，能骗到分就好。狗头.jpg

举个例子，一次模拟赛的时候，场均 \(T3\) 暴力 \(40pts\) ，而善于骗分的我搞到了 \(60pts\)，为什么呢？？？

看代码吧。。。

骗分代码

#include<bits/stdc++.h>
using std::cout; using std::endl;
#define try(i,a,b) for(register signed i=a;i<=b;++i)
#define throw(i,a,b) for(register signed i=a;i>=b;--i)
namespace xin_io
{
	#define scanf nb = scanf
	#define debug cout<<"debug"<<endl
	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<2,stdin),p1 == p2) ? EOF : *p1++
	char buf[1<<20],*p1 = buf,*p2 = buf,output[100]; FILE *xinnb;int nb;typedef long long ll; typedef unsigned long long ull;
	void openfile() {xinnb = freopen("t.txt","r",stdin);} void outfile() {xinnb = freopen("o.txt","w",stdout);}
	inline int get()
	{
		register int s = 0,f = 1; register char ch = gc();	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = gc();}
		while( isdigit(ch)) s = (s << 1) + (s << 3) + (ch xor 48),ch = gc();return s * f;
	}
	template<typename type>inline void write(type x)
	{
		if(!x) return putchar('0'),putchar('\n'),void(); if(x < 0) putchar('-'),x = -x;
		register int cnt = 0;while(x) output[++cnt] = x % 10,x /= 10; 
		throw(i,cnt,1) putchar(output[i] xor 48);return putchar('\n'),void();
	}
}
using namespace xin_io; static const int maxn = 1e7+10,inf = 1e9+7,mod = 123456789;
namespace xin
{
	class xin_edge{public:int ver,next;}edge[maxn];
	int head[maxn],zhi = 0;
	inline void add(int x,int y) {edge[++zhi].ver = y; edge[zhi].next = head[x]; head[x] = zhi;}
	int n,c[maxn],tot = 1;
	std::vector<int>wit;
	void dfs(int now,int col,int ms,int dep)
	{
		if(dep > ms) return ;
		c[now] = col; if(col) wit.push_back(now);
		if(col == 1) add(now,++tot),add(tot,now),dfs(tot,0,ms,dep+1);
		else
		{
			add(now,++tot),add(tot,now); dfs(tot,0,ms,dep+1);
			add(now,++tot),add(tot,now); dfs(tot,1,ms,dep+1);
		}
	}
	int top[maxn],hson[maxn],siz[maxn],d[maxn],fa[maxn];
	void dfs1(int x,int f)
	{
		d[x] = d[f] + 1; siz[x] = 1 ;fa[x] = f;
		for(register int i=head[x];i;i=edge[i].next)
		{
			register int y = edge[i].ver;
			if(y == f) continue;
			dfs1(y,x);
			siz[x] += siz[y];
			if(siz[y] > siz[hson[x]]) hson[x] = y;
		}
	}
	void dfs2(int x,int t)
	{
		top[x] = t;
		if(hson[x]) dfs2(hson[x],t);
		for(register int i=head[x];i;i=edge[i].next)
		{
			register int y = edge[i].ver;
			if(y == hson[x] or y == fa[x]) continue;
			dfs2(y,y);
		}
	}
	inline int lca(int x,int y)
	{
		while(top[x] xor top[y])
		{
			if(d[top[x]] < d[top[y]]) std::swap(x,y);
			x = fa[top[x]];
		}
		if(d[x] > d[y]) return y;return x;
	}
	ll ans[maxn];
	inline void pianfen(int x)
	{
		if(x == 20) cout<<"0 2584 5777 4557 7605 9022 11669 14829 18539 24232 29932 39068 48230 63004 77615 101103 124353 161124 198103 252565 307548 396301 478075 611861 728718 922724 1078302 1342082 1520084 1844655 1989813 2299701 2232598 2408279 1948339 1576239 0 0 0 0"<<endl;
		if(x == 21) cout<<"0 4181 9348 7374 12307 14601 18887 24005 30017 39245 48495 63330 78232 102307 126146 164738 202713 264511 323819 422659 510355 662171 804598 1037879 1251393 1602014 1907726 2415772 2822998 3513638 3979620 4829376 5209393 6020699 5845016 6304957 5100817 4126648 0 0 0 0"<<endl;
		if(x == 22) cout<<"0 6765 15126 11932 19915 23628 30566 38852 48589 63536 78532 102583 126786 165875 204738 267526 329961 430592 530384 689630 849133 1093162 1337647 1732639 2107038 2716853 3276413 4193986 4994574 6324524 7390738 9198802 10418792 12643464 13638373 15762391 15302452 16506591 13354113 10803704 0 0 0 0 "<<endl;
		if(x == 23) cout<<"0 10946 24475 19307 32225 38234 49463 62875 78639 102840 127132 166098 205342 268746 331861 433949 535569 700060 862665 1126695 1383953 1807734 2201400 2864363 3500485 4537055 5515724 7113163 8577537 10980139 13075882 16557868 19349170 24082798 27276740 33101025 35705719 41266479 40062338 43214817 34961521 28284465 0 0 0 0"<<endl;
		if(x == 24) cout<<"0 17711 39602 31240 52143 61867 80039 101745 127261 166435 205769 268866 332452 435185 537576 703160 868425 1135609 1401511 1830731 2257551 2942351 3626859 4697612 5767288 7496572 9165909 11877217 14440926 18622153 22456507 28746236 34233186 43349012 50656818 63049562 71411444 86659602 93478791 108037041 104884564 113137859 91530451 74049690 0 0 0 0"<<endl;
		if(x == 25) cout<<"0 28657 64078 50548 84371 100106 129512 164638 205933 269334 333006 435149 538118 704495 870414 1138794 1406889 1840626 2272638 2971832 3665969 4791540 5898360 7708953 9438484 12304948 15095008 19628708 23995141 31095905 37806262 48753779 58791675 75258764 89623562 113489236 9164449 41609129 63500787 103421001 121273858 35931071 27677774 49285183 116173042 70407817 0 0 0 0"<<endl;
		if(x == 26) cout<<"0 46368 103681 81789 136517 161978 209561 266401 333227 435828 538880 704200 870894 1140244 1408967 1843639 2278209 2981192 3682611 4816969 5947985 7775346 9595320 12524886 15451508 20090552 24720660 32208332 39523192 51386197 62821615 81409189 98978652 4181912 30462038 73573072 111180825 50205050 100293364 61777795 119090933 100146603 23429212 123212956 101605549 34717689 10075098 13716971 0 0 0 0 "<<endl;
		if(x == 27) cout<<"0 75025 167760 132338 220891 262089 339083 431057 539193 705221 871991 1139534 1409336 1845303 2280358 2984118 3687993 4826775 5963711 7803207 9638419 12608341 15563781 20352160 25089360 32805925 40304068 52614472 64709140 84328948 103469112 11076449 41010814 89676182 12215324 87249229 32594130 22003858 120462010 37125982 44802019 20267497 46858418 73562028 72470560 86794224 30225293 54867885 37509040 94199886 0 0 0 0"<<endl;
		if(x == 28) cout<<"0 121393 271442 214128 357411 424072 548654 697476 872453 1141108 1410976 1843919 2280554 2986111 3690302 4829442 5969097 7812924 9654784 12634582 15610869 20425142 25229202 32995367 40740236 53231877 65709546 85646604 105544532 14272963 45964327 97312823 23976022 105296584 60212928 64161259 61124901 10651714 67320661 115895096 3291741 61172828 34112739 122481455 21484337 120539472 70525686 13712922 112527121 6429176 102452023 21969108 0 0 0 0"<<endl;
	}
	inline short main()
	{
	#ifndef ONLINE_JUDGE
		openfile();
	#endif
		std::cin>>n;
		if(n > 19)
		{
			pianfen(n);
			return 0;
		}
		dfs(1,c[1]=1,n,1);
		dfs1(1,0); dfs2(1,1);
		try(i,0,wit.size()-1)
			try(j,i+1,wit.size()-1)
			{
				register int x = wit[i],y = wit[j];
				++ans[d[x] + d[y] - 2 * d[lca(x,y)]];
			}
		try(i,1,(n<<1))
			printf("%lld ",ans[i] % mod);
		return 0;
	}
}
signed main() {return xin::main();}

现在知道为啥

\(meet\;in\;middle\) 优化 XIN 算法

今天的一场考试让我痛定思痛，明明有 \(35pts\) 的二维XIN队板子却没有打对，挂成了可怜的 \(15pts\)，很是生气。

查看题解，发现全新思路！！！！

\(meet\;in\;middle\) 优化 XIN 算法

很是开心，然后发现可以解决 \(n \leq 40\) 范围的题目。

~~爆搜能力又增加了！！！~~

我们可以查看 P4799 [CEOI2015 Day2]世界冰球锦标赛这个题目。

我们发现似乎 \(XIN\) 算法似乎有一万分，然而。。。。

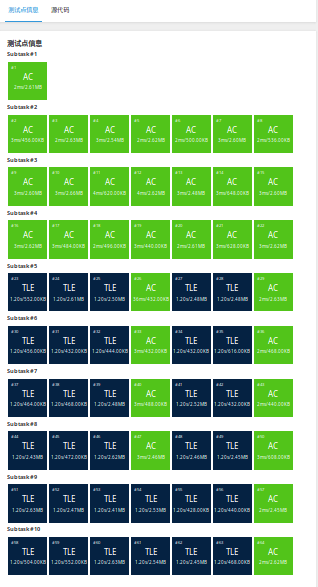
~~狂T不止~~

然而 \(meet\;in\;middle\) 之后：

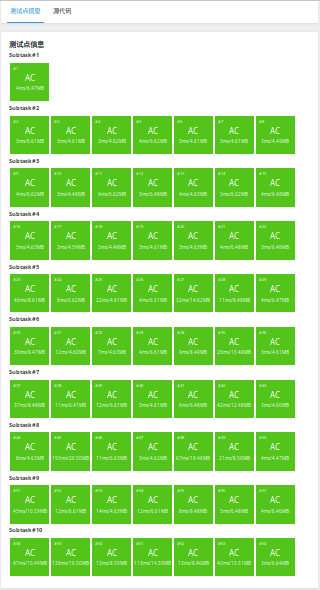
\(meet\;in\;middle\) 的思想就好比这两张图片：

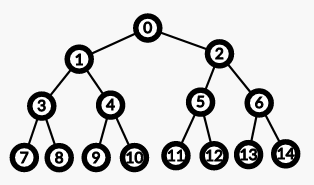
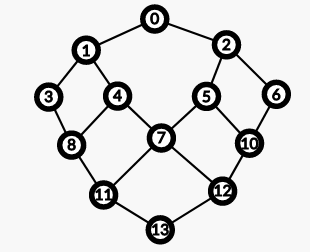
分开搜索，一定快，因为优化的是指数

复杂度：

\[\huge{\mathcal O(2^{\frac {n}{2}})} \]

好久好久没有写过这个玩意了。。。

然后昨天来了一个几乎很多人都不会打爆搜的题目。

然后我打了一个迭代加深，~~似乎就比 puts("-1")高 5 分~~

所以就来说一说迭代加深。

实际上其实就是一个普通的~~dfs~~XIN队。

根据昨天的题目:

我们要找到一个步数最小的方案。

但是我们的深度优先搜索会导致深度不断增大，也就是深度优先

这样如果我们刚开始就走错了。。。那就。。。

所以..

那么我们就开始限制步数。

while(!dfs(++dep));

这样就完了？？？

不，这是错的！！

为啥？？

应该这样

while(!xin_team(++dep));

\(\color{red}{perfect}\)

然后我们就限制了这个玩意的步数，只要 xin_team 的返回值为真，那么这个一定就是最优的答案。

所以，为啥不广搜呢？？

我不会告诉你这个题目迭代加深有15分，然后广搜有80的

完蛋的迭代加深

#include<bits/stdc++.h>
using std::cout; using std::endl;
#define try(i,a,b) for(register int i=a;i<=b;++i)
#define throw(i,a,b) for(register int i=a;i>=b;--i)
#define go(i,x) for(register signed i=head[x],y=edge[i].ver;i;i=edge[i].next,y = edge[i].ver)
namespace xin_io
{
    #define file(x) freopen(#x".in","r",stdin); freopen(#x".out","w",stdout);
	#define sb(x) std::cerr << #x" = "<<x<<' '
	#define jb(x) std::cerr << #x" = "<<x<<endl
	#define debug cout<<"debug"<<endl
	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1 ++
	#define scanf ak = scanf
	char buf[1<<20],*p1 = buf,*p2 = buf; using ll = long long; using ull = unsigned long long; int ak;
	class xin_stream{public:template<typename type>xin_stream operator >> (type &s)
	{
		s = 0; register bool f = 0; register char ch = gc();
		while(!isdigit(ch)) f |= ch == '-',ch = gc();
		while( isdigit(ch)) s = (s << 1) + (s << 3) + (ch xor 48),ch = gc(); return s = f ? -s : s,*this;
	}}io;
}
using namespace xin_io; static const int maxn = 1e6+10,two = 1e2+10,inf = 1e9+10;
#define int long long
namespace xin
{
	int n,m,qnum,cnt_w;
	bool hard[two][two];
	int goalx,goaly,nx,ny;
	const int dx[] = {1,-1,0,0},dy[] = {0,0,1,-1};
	bool dfs(int dep,int ex,int ey,int nowx,int nowy,int ms)
	{
//		sb(nowx); sb(nowy); sb(ex); sb(ey); jb(dep);
		if(nowx == ex and nowy == ey) return false;
		if(nowx == goalx and nowy == goaly) return true;
		else if(dep == ms) return false;
		if((nowx == ex and abs(nowy - ey) == 1) or (nowy == ey and abs(nowx - ex) == 1))
		{	
//			sb(nowx); sb(nowy); sb(ex); jb(ey);
			if(dfs(dep+1,nowx,nowy,ex,ey,ms)) return true;
		}
		try(i,0,3)
		{
//			sb(nowx); sb(nowy); sb(ex); jb(ey);
			nx = ex + dx[i]; ny = ey + dy[i];
			if(!hard[nx][ny] and nx <= n and nx >= 1 and ny <= m and ny >= 1)
				if(dfs(dep+1,nx,ny,nowx,nowy,ms)) return true;
		}
		return false;
	}
	int ex,ey,nowx,nowy;
	inline short main()
	{
		file(y);
		io >> n >> m >> qnum;
		try(i,1,n) try(j,1,m) io >> hard[i][j],hard[i][j] = !hard[i][j],cnt_w += !hard[i][j];
/*		try(i,1,n)
		{
			try(j,1,m)
				cout<<hard[i][j]<<' ';
			cout<<endl;
		}*/
		try(cse,1,qnum)
		{
			io >> ex >> ey >> nowx >> nowy >> goalx >> goaly;
//			sb(goalx); jb(goaly);
			if(hard[goalx][goaly]) {puts("-1"); continue;}
			int ans = 0;
			while(!dfs(0,ex,ey,nowx,nowy,++ans))
			{
//				cout<<endl;
//				if(ans == 2) break;
//				if(ans > cnt_w) {puts("-1"); break;}
//				jb(ans);
				if(clock() > 0.4* CLOCKS_PER_SEC) {ans = -1; break;}
			}
			cout<<ans<<endl;
		}
		return 0;
	}
}
signed main() {return xin::main();}

~~主要是这个玩意我不知道该如何判断无解的情况。。~~

niuma兵

手动 @niuma兵

XIN* 算法

这个玩意实在不是很简单。

所以只能口胡。

如果让我们人脑完成一个搜索，那么我们一定会自动排除一些垃圾的状态。

这样的计算量会减少很多很多。

所以我们应该使计算机也有这个功能才好。

然后我们就可以设置强大的估价函数

这个玩意就是我们按照这个值的大小来决定我们的选择顺序。

这个估价函数设置成什么就得看自己的造化了。

然后每次把新搜索到的状态扔到 priority_queue 里面就好了。

posted @ 2021-07-29 20:31 NP2Z 阅读(830) 评论(23) 编辑收藏举报

刷新页面返回顶部

XIN

XIN队算法

XIN队算法

\(newly\;upd:2021.10.18\)

\(newly\;upd:2021.8.4\)

\(newly\;upd:2021.8.1\)

\(newly\;upd:2021.7.8\)

\(newly\;upd:2021.6.6\)

OI至高算法，只要XIN队算法打满，保证所有比赛 \(rk1\)，碾爆标程，让对手望尘莫及。

请慎用

注：名称由莫队算法改编而来

XIN队算法：

优化XIN队算法：

非常不建议使用

复杂度:

还附加超大常数

XIN队算法升级：二维XIN队

我们发现，对于一般的题目，大多是 \(dp\) 解决，然而纯粹运用上述方法只能拿到部分分数，甚至全部 \(TLE\) 所以，记忆化 \(XIN\) 队算法应运而生。

\(XIN\) 优化分块预处理

鉴于有童鞋想要学习 clock() 骗分优化方法，那就更新一下下

打表骗分方法

\(meet\;in\;middle\) 优化 XIN 算法

\(meet\;in\;middle\) 优化 XIN 算法

所以，为啥不广搜呢？？

我不会告诉你这个题目迭代加深有15分，然后广搜有80的

XIN* 算法

公告