DS博客作业06--图

DS博客作业06--图

1.本周学习总结

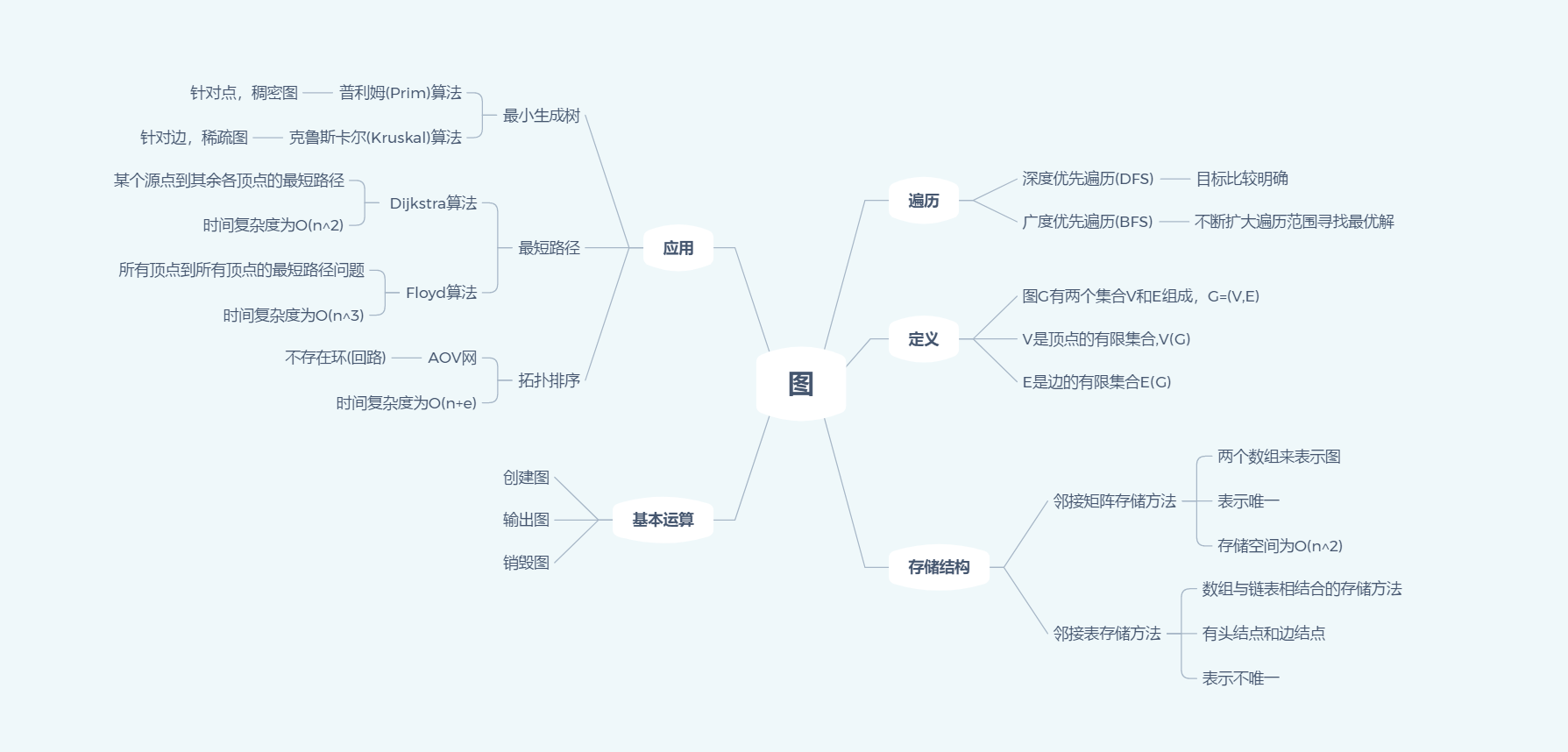
• 本周学习了有关图的知识，图和前面的树还是有很大的联系，图可以转化为对应的生成树，但图和树又有一些本质上的不同，在数的结构中元素之间有明显的层次关系，每一层上的数据元素能和下一层中多个元素相关，但只能和上一层中一个元素相关，而在图的结构中则不同，图中结点之间的关系可以是任意的，其中任意两个数据元素之间都可能相关；
• 图的深度优先遍历和广度遍历方式是图遍历的两种基本算法 ，也是用图来解决很多问题的优点所在，虽然两种遍历的代码量和时间复杂度的差不多，但深度优先遍历更适合目标比较明确，以找到目标为主要目的的情况，而广度优先遍历更适合在不断扩大遍历范围时找到相对最优解的情况；
• 图构造最小生成树是图的重要应用之一，其中Prim算法和Kruskal算法是寻找最小生成树最常用的两种算法，Prim算法从图中顶点的最短权值边入手，逐步生成最小生成树，所以在边数非常多如稠密图的情况下会更好一些。Kruskal算法克鲁斯卡尔算法主要是针对边来展开，所以在边数少如稀疏图时效率会非常高，所以对于稀疏图有很大的优势；
  

2.PTA实验作业

2.1.题目1： 图着色问题

void CreateAdj
定义i,j,k
创建新结点p
for k=1 to k<=n
then 将k置为顶点信息
给所有头结点的指针域置初值
end
for k=0 to k<e
输入i,j
创建新结点p
j存放邻结点
p指向邻接表的头指针
头指针移动
创建新结点p
i存放邻结点
p指向邻接表的头指针
头指针移动
end

void IsTure
创建新结点p
定义set容器
定义i,flag=0,初始化a[G->n]为0
for i=1 to i<=G->n
then 输入a[i]
s.insert(a[i])
end 
if s.size()≠k flag=1
else
for i=0 to i<=G->n
then p指向邻接表的头指针
while p≠NULL
if a[p->adjvex=a[i]
flag=1 break
end if
p指向下一个结点
end for
if flag=0
输出Yes

2.1.2代码截图

2.1.3本题PTA提交列表说明

Q1：开始不知道怎么去记录分配过的颜色的数目，试了很多方法都不可行
A1：在问了同学了，去学习了set容器的用法，问题就解决了。

2.2 题目2：六度空间

定义n,m
定义二维数组 a[10001][10001]
                     queue[10001]={0}
                     flag[10001]={0}
输入n,m
for int i=0 to i<m
then 定义x,y
输入x,y
a[x][y]=1,a[y][x]=1
end for
for i=1 to i<=n
定义计数器count=1
定义length记录长度
定义p指向一层的最后一个结点
定义 h=0,t=0
for int k=0 to k<10001
queue[k]=0
flag[k]=0
将i进队
标记以访问
while h≠t且length<6
遍历i长度小于6的子节点
遍历x的子节点
for int j=1 to j<=n
then if a[x][j]==1且flag[j]==0)
j进队
t++
标记访问
i的计数器加1
end for
if x是层尾节点
p=queue[(t-1)%10001];
长度+1
end
double ratio=count/n
输出结果

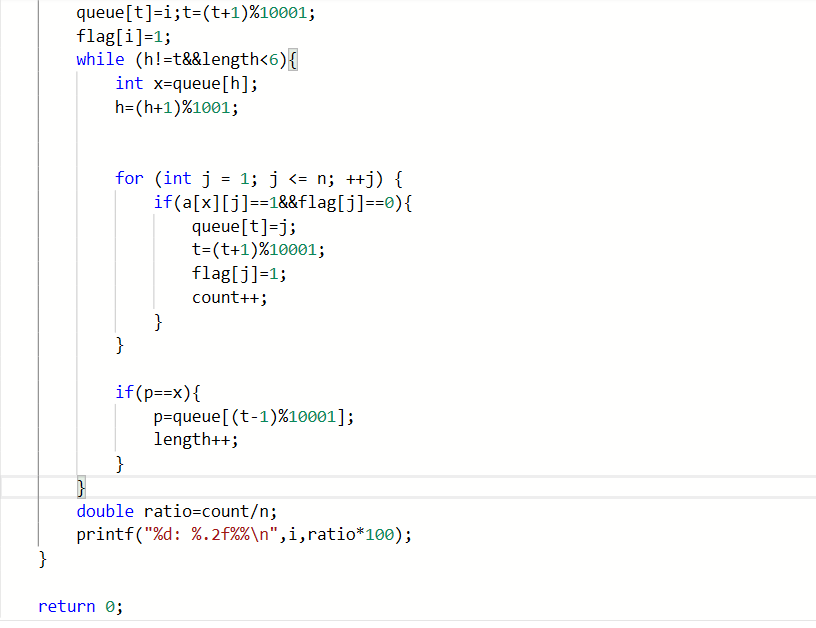
2.2.2代码截图

2.2.3本题PTA提交列表说明

Q1：定义的二维数组在结点个数过多时会直接崩溃，导致程序无法运行
A1：直接定义那么长的数组会导致运行错误，把数组拿出来定义为静态，这样分配到的存储空间会大很多。

2.3 题目3：公路村村通

2.3.1设计思路

int main
int num1,num2,price,road
输入n,road
调用memset函数为数组a置初值
while(road--)
then 输入 num1,num2,price
a[num1][num2]⬅price
a[num2][num1]⬅price
end
for int i=1 to i<=n
a[i][i]=0
end 
for i=1 to i<=n
调用memset函数为数组book置初值
book[i]=1
调用dfs函数
end
if(exs) 输出mini
else 输出-1

void dfs
if 输入数据不足以保证畅通 return 
if cnt=n-1
ext=1
mini⬅num
return
end
cnt+1
for i=1 to i<=n
if book[i]=0且a[c][i]>=1
then book[i]=1
调用函数dfs
book[i]=0
end 

2.3.2代码截图

2.3.3本题PTA提交列表说明

Q1：在深度遍历的中间出现错误
A1：在深度遍历的时候，num不能在调用函数之前更新，更应该在调用的时候直接传入更新后的num，改变num更新的位置就可以了。

3、上机考试错题及处理办法

3.1 错题代码截图

题目：拓扑排序
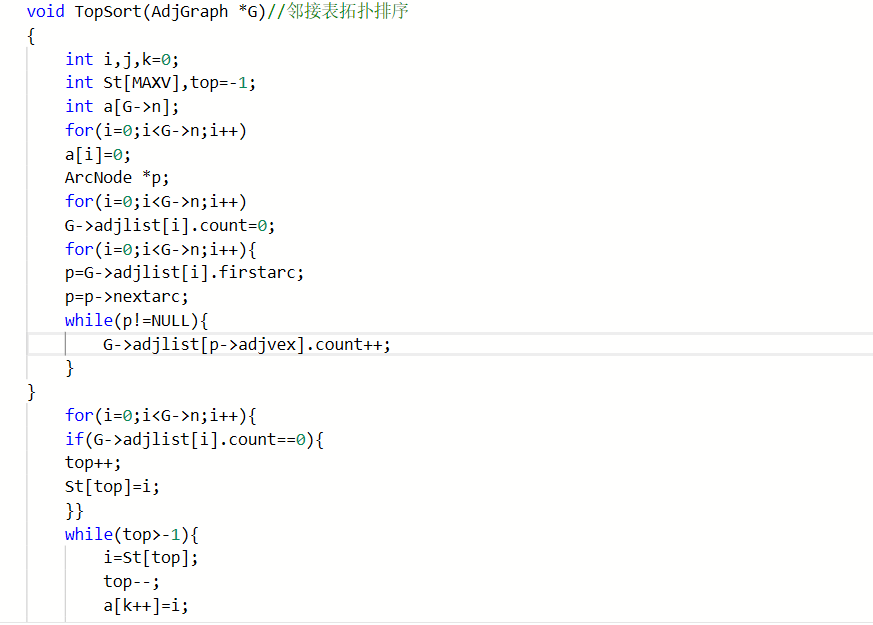
错误代码：

3.2 错的原因及处理方法

原因：在求所有顶点入度的时候，在保存了第一个邻接点以后，误将p指向了下一个结点，导致整个图的创建出现问题。
处理方式：在求所有顶点入度的循环中，p=G->adjlist[i].firstarc保存了图的第一个邻接点后，应该进行p是否为空的判断，在p不为空时,count+1,且这个时候p才指向下一个结点，将p=p->nextarc这条语句放到while(p!=NULL)里面以后就正确了。
正确代码截图：