C程序设计实验报告
姓名:陈中笑 实验地点:一教524 实验时间:2021.5.27
一、实验目的与要求
1、掌握函数的定义方法和调用规则。
2、掌握在c语言中主调函数和被调函数之间进行数据传递的规则。
3、了解函数的返回值及其类型,并正确使用。
4、了解局部变量和全局变量的作用域及它们与存储分类的关系,理解变量的存在性和可见性的概念。
5、练习递归函数的使用。
二、实验内容
1.实验练习:6.3.1.3
问题描述
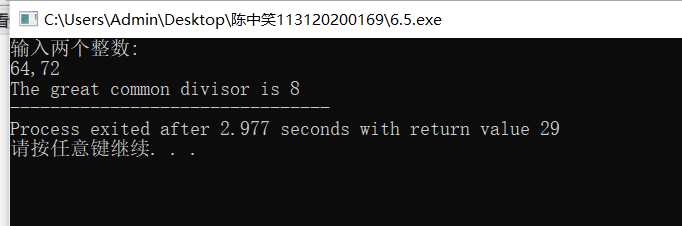
编写程序,从键盘输入两个整数,调用gcd()函数求它们的最大公约数,并输出结果。
实验代码:
#include <stdio.h>
int gcd(int a,int b)
{
int temp;
int remainder;
if(a<b)
{
temp=a;a=b;b=temp;
}
remainder=a%b;
while(remainder!=0)
{
a=b;
b=remainder;break;
}
return b;
}
int main()
{
int x,y;
int fac;
printf("输入两个整数:\n");
scanf("%d,%d",&x,&y);
fac=gcd(x,y);
printf("The great common divisor is %d",fac);
}
问题分析
- 跟着流程图走没有很大问题,但涉及到数据交换和辗转相除法,有点难理解
2.实验练习:6.3.2.1
问题描述
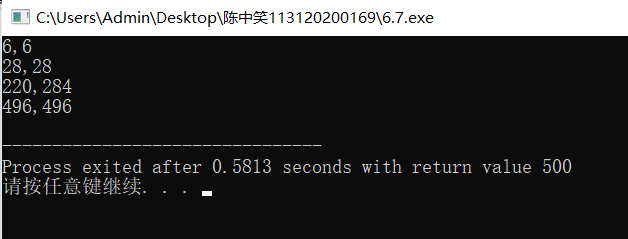
若正整数 A 的所有因子( 包括 1 但不包括自身,下同)之和为 B ,而 B 的因子之和为 A,则称 A 和 B 为一对亲密数。例如,6的因子之和为1+2+3=6,因此6与6为一对亲密数。求出500以内的所有亲密数对。
实验代码
#include <stdio.h>
int facsum(int m)
{
int sum=1,f=2;
while(f<=m/2)
{
if(m%f==0)
sum=sum+f;
f++;
}
return sum;
}
int main()
{
int m=3,n,k;
while(m<=500)
{
n=facsum(m);
k=facsum(n);
if(m==k&&m<=n)
printf("%d,%d\n",m,n);
m++;
}
}
问题分析
- 要先理解亲密数对的概念,然后再看流程图,再写代码。
3.实验练习:6.3.2.3
问题描述
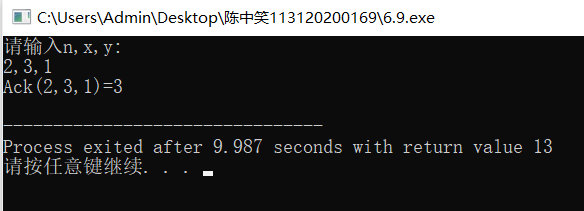
根据方法说明,计算Ackerman函数。
实验代码
#include<stdio.h>
int Ack(int n,int x,int y)
{
int a;
if(n==0)
a=x+1;
else if(n==1&&y==0)
a=x;
else if(n==2&&y==0)
a=0;
else if(n==3&&y==0)
a=1;
else if(n>=4&&y==0)
a=2;
else if(n!=0&&y!=0)
a=Ack(n-1,Ack(n,x,y-1),x);
return a;
}
main()
{
int n,x,y,result;
printf("请输入n,x,y:\n");
scanf("%d,%d,%d",&n,&x,&y);
if(n<0||x<0||y<0)
printf("error!");
else
result=Ack(n-1,Ack(n,x,y-1),x);
printf("Ack(%d,%d,%d)=%d\n",n,x,y,result);
}
问题分析
- 回归条件比较多,一开始在if的分支结构中,没有写else,导致结果错误,后经过同学提醒成功得到正确答案。
4.实验练习:6.3.3.1
问题描述
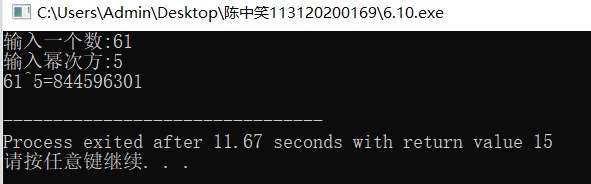
编写程序,分别从键盘输入数据x和y,计算x的y次幂并输出。
实验代码
#include<stdio.h>
long getpower(int x,int y)
{
if(y==1)
return x;
else if(y>=2)
return x*getpower(x,y-1);
}
int main()
{
int num,power;
long answer;
printf("输入一个数:");
scanf("%d",&num);
printf("输入幂次方:");
scanf("%d",&power);
answer=getpower(num,power);
printf("%d^%d=%ld\n",num,power,answer);
}
问题分析
- 只有能写出递归算法的数学模型,才能编写出递归函数。
三、什么是辗转相除法
(答案摘自百度知道)
辗转相除法, 又名欧几里德算法(Euclidean algorithm),是求最大公约数的一种方法。它的具体做法是:用较大数除以较小数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。
如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。另一种求两数的最大公约数的方法是更相减损法。
四、实验小结
1、通过自己上手实验对函数的定义和调用有了进一步的认识。
2、更加清楚的明白了自己的不足,有些题虽然对着流程图能打出代码但不懂代码的意义以及代码如何运行。
五、近期个人学习小结
通过学习这门课程了解了许多内容,但逻辑思维能力还是有些不足。
我的复习计划主要是从书本出发,看题、写代码,搞懂每一个知识点。
希望老师讲解一些比较重要的习题。





