《算法图解》——第九章 动态规划
第九章 动态规划
1 动态规划——背包问题
公式：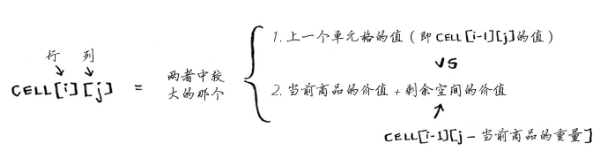
练习
9.1 假设你还可偷另外一件商品——MP3播放器，它重1磅，价值1000美元。你要偷吗？
要。在这种情况下，你可偷来MP3播放器和iPhone和吉他，总价值为4500美元
行的排列顺序发生变化时结果如何？答案没有变化。也就是说，各行的排列顺序无关紧要。
可以逐行而不是逐列填充网格吗？就这个问题而言，这没有任何影响，但对于其他问题，可能有影响。
增加一件更小的商品将如何呢？你需要考虑的粒度更细，因此必须调整网格。
可以偷走商品的一部分吗？答案是没法处理。使用动态规划时，要么考虑拿走整件商品，要么考虑不拿，而没法判断该不该拿走商品的一部分。但是贪婪算法可以轻松处理！
2 旅行行程最大化
根据清单画动态规划网格：
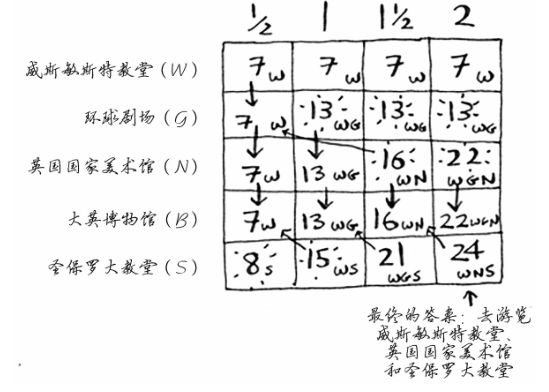
如何处理相互依赖的情况？
动态规划功能强大，它能够解决子问题并使用这些答案来解决大问题。但仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。
计算最终的解时会涉及两个以上的子背包吗？
为获得前述背包问题的最优解，可能需要偷两件以上的商品。但根据动态规划算法的设计，最多只需合并两个子背包，即根本不会涉及两个以上的子背包。不过这些子背包可能又包含子背包。
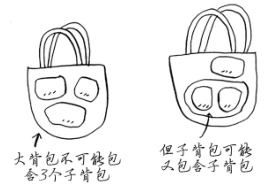
最优解可能导致背包没装满吗？of course
练习
9.2 假设你要去野营。你有一个容量为6磅的背包，需要决定该携带下面的哪些东西。其中每样东西都有相应的价值，价值越大意味着越重要：
水（重3磅，价值10）；
书（重1磅，价值3）
食物（重2磅，价值9）；
夹克（重2磅，价值5）；
相机（重1磅，价值6）。
请问携带哪些东西时价值最高？用动态规划做呗，水，食物，相机
3 最长公共子串
动态规划的启示：
①动态规划可帮助你在给定约束条件下找到最优解。
②在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。
③每种动态规划解决方案都涉及网格。
④单元格中的值通常就是你要优化的值。
⑤每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网格的坐标轴。
举个🌰：Alex输入了hish，那他原本要输入的是fish还是vista呢？
3.1 绘制网格
解决上面问题的网格应该怎么构建，要考虑下面几点：
①单元格中的值是什么？在这个例子中，你要找出两个单词的最长公共子串，这就是你要计算的值。
②如何将这个问题划分为子问题?你可能需要比较子串：不是比较hish和fish，而是先比较his和fis。
③网格的坐标轴是什么？每个单元格都将包含这两个子串的最长公共子串的长度。这也给你提供了线索，让你觉坐标轴很可能是这两个单词。
因此，网格可能类似于下面这样：
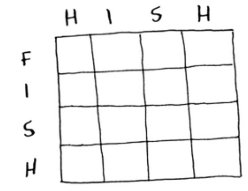
3.2 填充网格
填充时用什么公式呢？费曼算法（Feynman algorithm）步骤如下：（这怕不是再说废话= =！废慢算法？）
①将问题写下来
②好好思考
③将答案写下来
3.3 揭晓答案
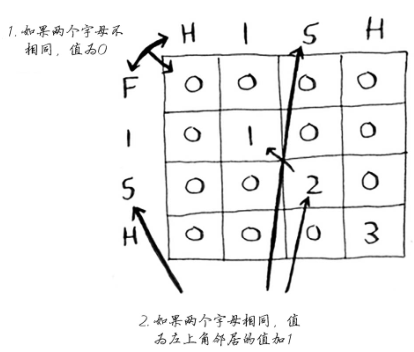
查找单词hish和vista的最长公共子串时，网格如下：
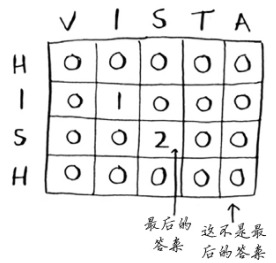
对于背包问题，最终答案总在最后的单元格中；但对于最长公共子串而言，答案是网格中最大的数字——不一定在最后的单元格中。
那么问题的答案出来了，hish和fish的最长公共子串包含三个字母，而hish和vista的最长公共子串包含两个字母。因此Alex很可能原本要输入的是fish。
3.4 最长公共子序列
假设Alex不小心输入了fosh，他原本想输入的是fish还是fort呢？我们使用最长公共子串公式来比较它们：
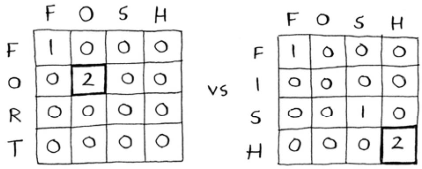
所以都为2，长度相同，但是fosh和fish更像。
这里应该比较最长公共子序列：两个单词中都有的序列包含的字母数。
3.5 最长公共子序列之解决方案
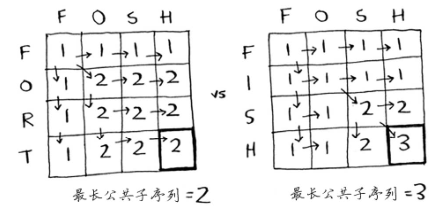
上图的公式：
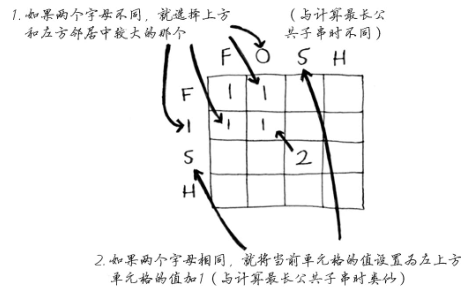
动态规划的实际应用：
①生物学家根据最长公共序列来确定DNA链的相似性，进而判断度两种动物或疾病有多相似。最长公共序列还被用来寻找多发性硬化症治疗方案。
②你使用过诸如 git diff 等命令吗？它们指出两个文件的差异，也是使用动态规划实现的。
③前面讨论了字符串的相似程度。编辑距离（levenshtein distance）指出了两个字符串的相似程度，也是使用动态规划计算得到的。编辑距离算法的用途很多，从拼写检查到判断用户上传的资料是否是盗版，都在其中。
④你使用过诸如Microsoft Word等具有断字功能的应用程序吗？它们如何确定在什么地方断字以确保行长一致呢？使用动态规划！
练习
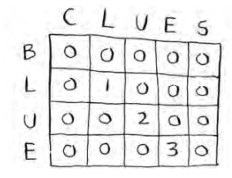
9.3 请绘制并填充用来计算blue和clues最长公共子串的网格。
4 小结
①需要在给定约束条件下优化某种指标时，动态规划很有用。
②问题可分解为离散子问题时，可使用动态规划来解决。
③每种动态规划解决方案都涉及网格。
④单元格中的值通常就是你要优化的值。
⑤每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。
⑥没有放之四海皆准的计算动态规划解决方案的公式。
