2023-07-07 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(三).md
2023-07-07 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(三)
1. 牛顿法
书接上回,对于一维最优化问题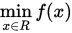 , 牛顿法是在迭代点处进行二次泰勒展开来近似原函数,然后求泰勒展开式的极小点,具体如下
, 牛顿法是在迭代点处进行二次泰勒展开来近似原函数,然后求泰勒展开式的极小点,具体如下
设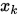 为当前迭代点,
为当前迭代点,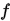 在
在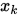 处的二阶泰勒展开式为
处的二阶泰勒展开式为
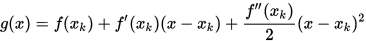
为了求近似函数
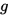 的最小值,考虑最优性条件
的最小值,考虑最优性条件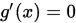 , 得到
, 得到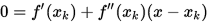
令
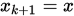 , 整理可得
, 整理可得
牛顿法要求目标函数二阶可导,且根据上述推导可知牛顿法收敛到
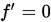 的点,即可能是极小点也可能是极大点, 只有当初始点和极小点比较接近(至少比到极大点更接近),才能收敛到极小点.
的点,即可能是极小点也可能是极大点, 只有当初始点和极小点比较接近(至少比到极大点更接近),才能收敛到极小点.
- % 一维最优化问题的牛顿法
- % fun 目标函数, 可以是符号函数或函数句柄
- % epsil 指定终止条件(精度)
- % maxIt 最大迭代次数
- function [xk xlog] = OneNewton(f, x0, epsil, maxIt)
- k = 0;
- if isa(f,'function_handle')
- syms x;
- fun(x) = f(x);
- else
- fun = f;
- end
- diff_fun1 = diff(fun);
- diff_fun2 = diff(diff_fun1);
- diff_fun1_h = matlabFunction(diff_fun1);
- diff_fun2_h = matlabFunction(diff_fun2);
- while k <= maxIt
- xk = x0 - diff_fun1_h(x0) / diff_fun2_h(x0);
- if abs(xk- x0) <= epsil
- break;
- end
- k = k + 1;
- x0 = xk;
- xlog(k) = xk;
- end
- end
测试代码
- f = @(x) sin(x);
- epsil = 1e-6;
- maxIt = 1e3;
- plot((-10):0.01:10, f((-10):0.01:10))
- x0 = 1;
- [xk xlog] = OneNewton(f, x0, epsil, maxIt)
- x0 = 0.5;
- [xk xlog] = OneNewton(f, x0, epsil, maxIt)
- x0 = -0.5;
- [xk xlog] = OneNewton(f, x0, epsil, maxIt)
2. 抛物线法
牛顿法要求目标函数二次可导,而抛物线法则没有此要求,其主要思想是插值一个二次多项式来近似代替目标函数.
给定第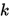 次的搜索区间
次的搜索区间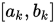 , 任意选取
, 任意选取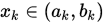 , 然后在
, 然后在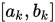 上取二次插值多项式
上取二次插值多项式
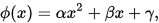
其满足
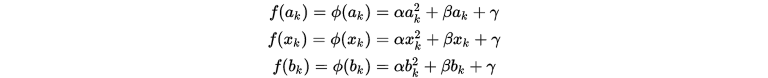
根据上述方程可以确定近似函数
 :
: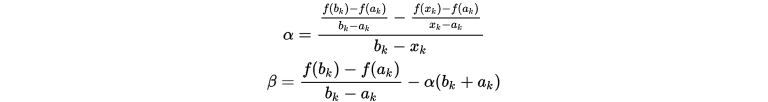
由于只需要知道二次函数的最值所在点,因此不需要知道
 的具体取值,令
的具体取值,令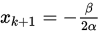 .
.
抛物线法有如下缺点
1. 可能不收敛. 如果新的迭代点和当前迭代点充分接近,但是新迭代点并不是目标函数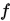 的极小点,则算法不收敛.
的极小点,则算法不收敛.
2. 选择的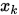 需要满足
需要满足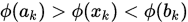 , 但是没有提供一种满足此条件的方法.
, 但是没有提供一种满足此条件的方法.
抛物线法的原理导致其不能简单改进到适用于所有情况的一维搜索中.
抛物线法
Step 1. 给定初始区间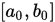 , 选取
, 选取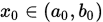 , 给出误差
, 给出误差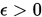 , 置
, 置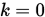 .
.
Step 2. 按照上面的公式计算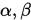 , 然后计算
, 然后计算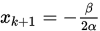 . 若
. 若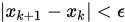 , 停止算法,输出
, 停止算法,输出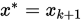 ; 否则转下步.
; 否则转下步.
Step 3. 若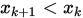 , 令
, 令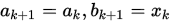 ; 若
; 若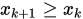 , 令
, 令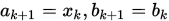 .
.
抛物线法的实现只需要带入公式即可,没有特殊之处,这里不给出程序。考虑抛物线法和其他方法的结合或许更有意义.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号