dp题单-背包问题

1、Cut Ribbon

思路一:数据范围很小，考虑直接枚举。

#include<bits/stdc++.h>
#define int long long
using namespace std;

int n, p, q, r;

signed main(){
    cin >> n >> p >> q >> r;
    int ans = 0;
    for(int i = 0; p * i <= n; i ++){
        for(int j = 0; p * i + q * j <= n; j++){//第二层for循环枚举的时候，要包含i的范围
            if((n - i * p - j * q) % r == 0){
                ans = max(ans, i + j + (n - i * p - j * q) / r);
            }
        }
    }
    cout << ans << endl;
    return 0;
}

思路二、考虑背包
完全背包（物品件数没有上限）。物品件数表示价值，长度表示体积。正常完全背包就可以。

2、Marvolo Gaunt's Ring

思路：每个位置上的数有两种状态，选或者不选，选了作为第几个数，作为第一个数？作为第二个数？作为第三个数？当前状态会与前一位的状态有关，考虑 $dp$ 。
$dp[i][j]$ ：前 $i$ 个数，选择 $j$ 个时的最优解。当 $j = 0$ 时， $dp[i][0]$ 表示 $ai \times p$ 的最优解。 $j = 1，j = 2$ 与之类似。

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N = 1e5 + 10;
int dp[N][3], a[N], n, p, q, r;

signed main(){
    cin >> n >> p >> q >> r;
    memset(dp, -0x3f, sizeof dp);
    for(int i = 1; i <= n; i++){
        cin >> a[i];
    }
    for(int i = 1; i <= n; i++){
        dp[i][0] = max(dp[i - 1][0], p * a[i]);
        dp[i][1] = max(dp[i][0] + a[i] * q, dp[i - 1][1]);//当j = 1时，要从dp[i][0]选
        dp[i][2] = max(dp[i][1] + a[i] * r, dp[i - 1][2]);
    }
    cout << dp[n][2] << endl;
    return 0;
}

3、Dima and Salad

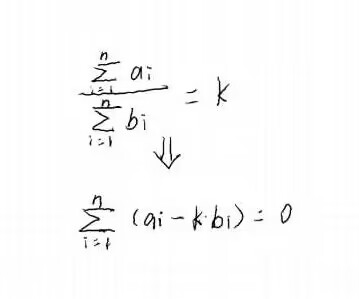
小总结：遇到公式的时候，先对公式进行化简。
思路：把 $a_i - k \times b_i$ 作为体积，价值为 $a_i$ 。但是题目中的每个i对应的体积可能有正有负，这时候分别处理正负两种情况。我觉得这个地方是整道题思路最妙的地方。值得学习。
题解：https://www.luogu.com.cn/problem/solution/CF366C