2018-2019-20172321 《Java软件结构与数据结构》第八周学习总结
2018-2019-20172321 《Java软件结构与数据结构》第八周学习总结
教材学习内容总结
第12章 优先队列与堆
一、概述
- 堆
- 堆的前提就是他首先是一个完全二叉树,其次就是满足要约束元素之间的关系。(对于堆中的每一个结点,该结点都小于或等于(大于或等于)它的左右孩子。)
- 优先队列
- 在前几周的学习中我们了解了队列的知识点,最主要的就是FIFO原则,但是优先队列就与我们原先学习的队列相比就多了一个规则,就是优先级高的就算后入对也要比优先级低的元素先出队,只有在优先级相同的时候才会遵循FIFO的原则;

二、堆的操作
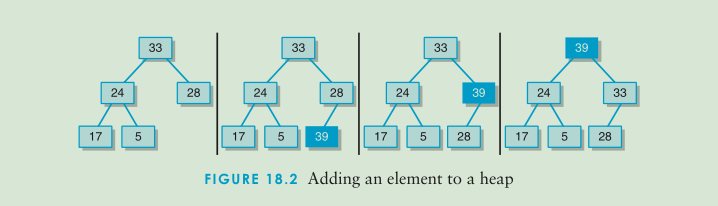
- addElement操作
将给定的元素添加到堆中的恰当位置,维持该堆的完全性属性和有序属性。
如果元素不是Comparable类型的,则会抛出异常。这是为了让元素可比较,可以维持堆的有序属性。
public void addElement(T obj) {
if (count == tree.length)
expandCapacity();
tree[count] = obj;
count++;
modCount++;
if (count > 1)
heapifyAdd();
}
private void heapifyAdd() {
T temp;
int next = count - 1;
temp = tree[next];
while ((next != 0) &&
(((Comparable) temp).compareTo(tree[(next - 1) / 2]) < 0)) {
tree[next] = tree[(next - 1) / 2];
next = (next - 1) / 2;
}
tree[next] = temp;
}
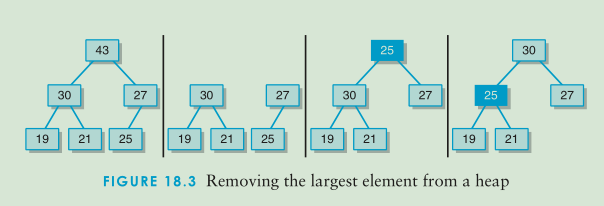
- removeMin操作
删除堆的最小元素:删除堆的最小元素并且返回。
最小元素位于根结点,删除掉根结点,为了维持树的完全性,要找一个元素来替代它,那么只有一个能替换根的合法元素,且它是存储在树中最末一片叶子上的元素。最末的叶子是h层上最右边的叶子。
public T removeMin() throws EmptyCollectionException {
if (isEmpty())
throw new EmptyCollectionException("ArrayHeap");
T minElement = tree[0];
tree[0] = tree[count - 1];
heapifyRemove();
count--;
modCount--;
return minElement;
}
/**
* Reorders this heap to maintain the ordering property
* after the minimum element has been removed.
*/
private void heapifyRemove() {
T temp;
int node = 0;
int left = 1;
int right = 2;
int next;
if ((tree[left] == null) && (tree[right] == null))
next = count;
else if (tree[right] == null)
next = left;
else if (((Comparable) tree[left]).compareTo(tree[right]) < 0)
next = left;
else
next = right;
temp = tree[node];
while ((next < count) &&
(((Comparable) tree[next]).compareTo(temp) < 0)) {
tree[node] = tree[next];
node = next;
left = 2 * node + 1;
right = 2 * (node + 1);
if ((tree[left] == null) && (tree[right] == null))
next = count;
else if (tree[right] == null)
next = left;
else if (((Comparable) tree[left]).compareTo(tree[right]) < 0)
next = left;
else
next = right;
}
tree[node] = temp;
}
- findMin操作
直接的返回根中的元素就可以
public T findMin() throws EmptyCollectionException {
if (isEmpty())
throw new EmptyCollectionException("ArrayHeap");
return tree[0];
}·
三、优先级队列
- 遵循两个排序规则:
- 具有更高优先级的项目在先。
- 具有相同优先级的项目使用先进先出方法来确定顺序。
- 虽然最小堆根本就不是一个队列,但是它却提供了一个高效的优先级队列实现。
四、用链表实现堆
- addElement操作
- 达到3个目的:在恰当位置处添加一个新的元素;对堆进行重排序以维持排序属性;将lastNode指针重新设定为指向新的最末结点
- 其使用了两个私有方法
- getNextParentAdd:它返回一个指向某结点的引用,该结点为插入结点的双亲
- heapifyAdd:完成对堆的任何重排序,从那片新叶子开始向上处理至根处
添加元素对于复杂度(复杂度为:2*logn + 1 +logn,即o(logn)):
- removeMin 操作
- 达到3个目的:用存储在最末结点处的元素替换存储在根处的元素;对堆重排序;返回初始的根元素。
- 其使用了两个私有方法
- getNewLastNode:它返回一个指向某一结点的引用,该结点是新的最末结点
- heapifyRemove:进行重排序(从根向下)
删除根元素对于复杂度(复杂度为:2*logn + logn + 1,即o(logn))
- findMin操作
- 该元素在堆根处,只需返回根处即可
复杂度为o(1)
五、用数组实现堆
- addElement操作:
- 在恰当位置处添加新结点。
- 对堆进行重排序以维持其排序属性。
- 将count值递增1。
时间复杂度为 1 + log ,为 O(logn)。
- removeMin操作
- 用存储在最末元素处的元素替换存储在根处的元素。
- 对堆进行重排序。
- 返回初始的根元素,并将count值减1。
时间复杂度为 1 + log ,为 O(logn)。
- findMin操作
- 指向索引为0
时间复杂度为O(1)。
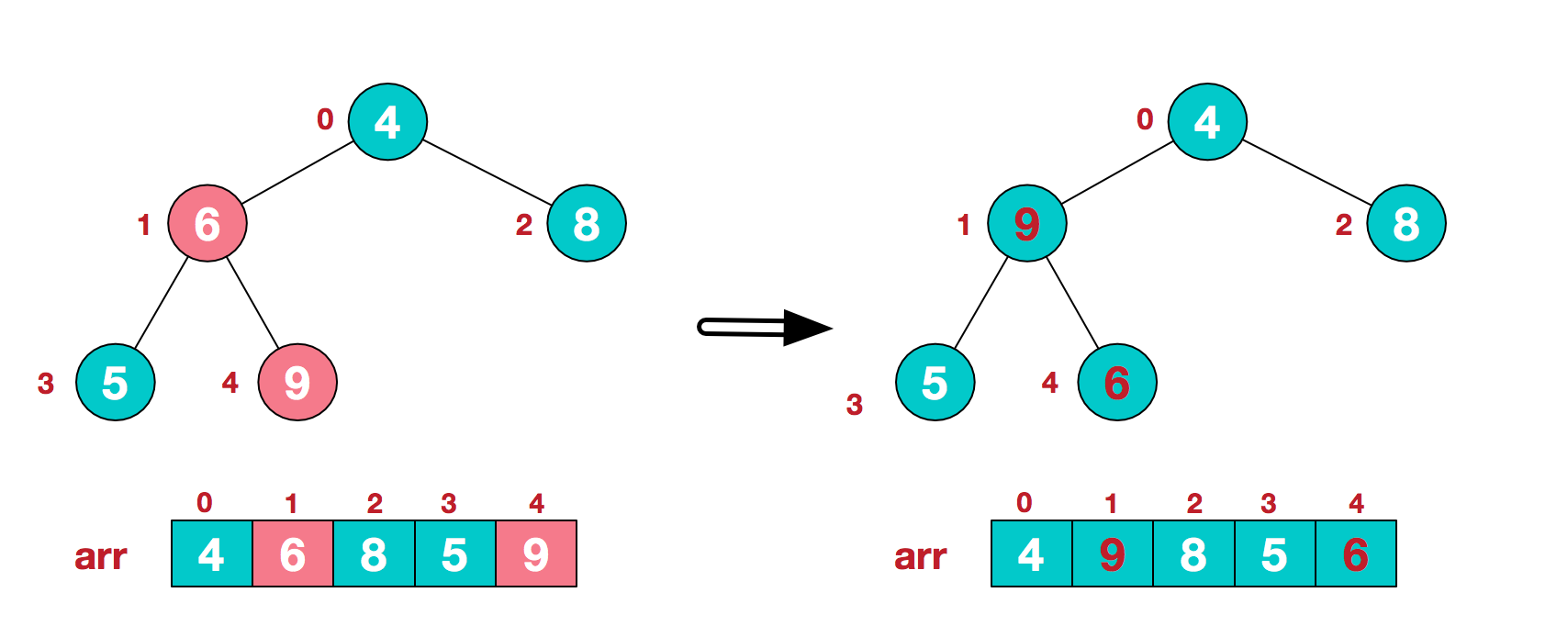
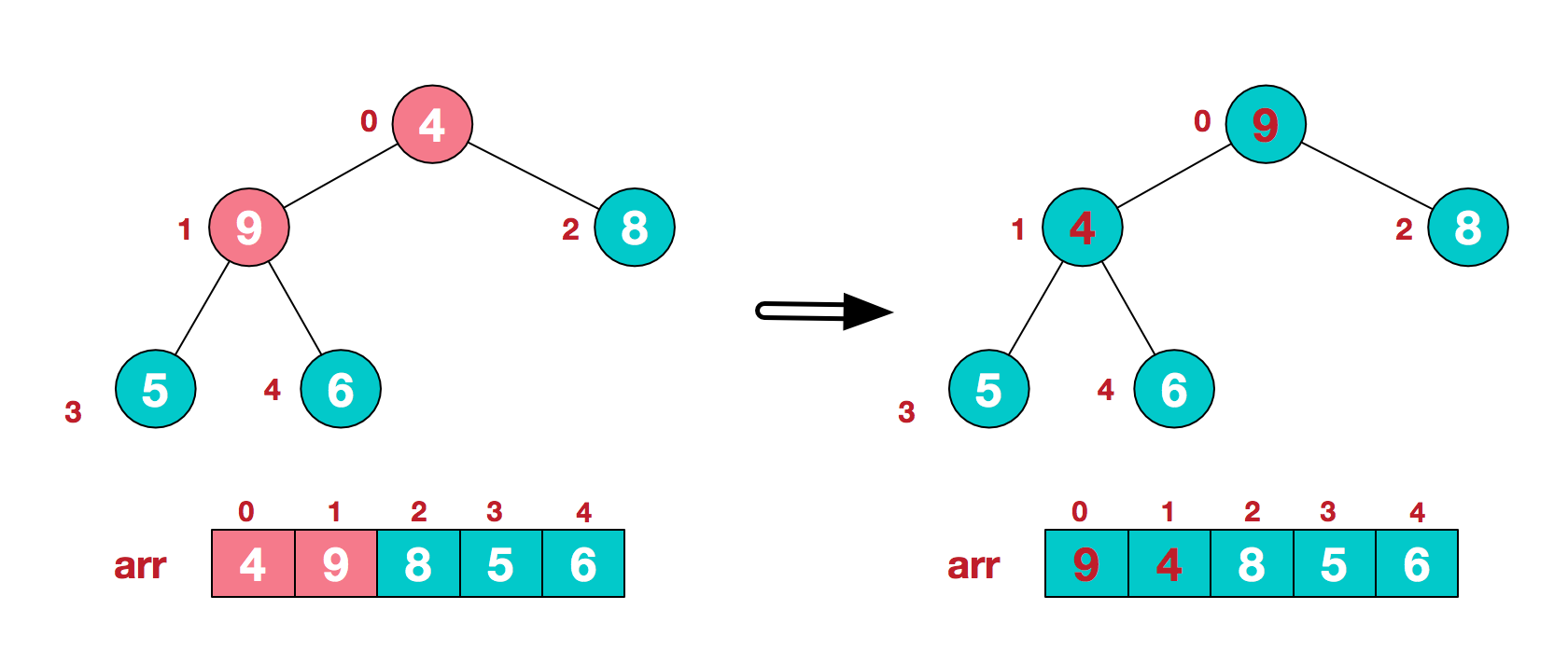
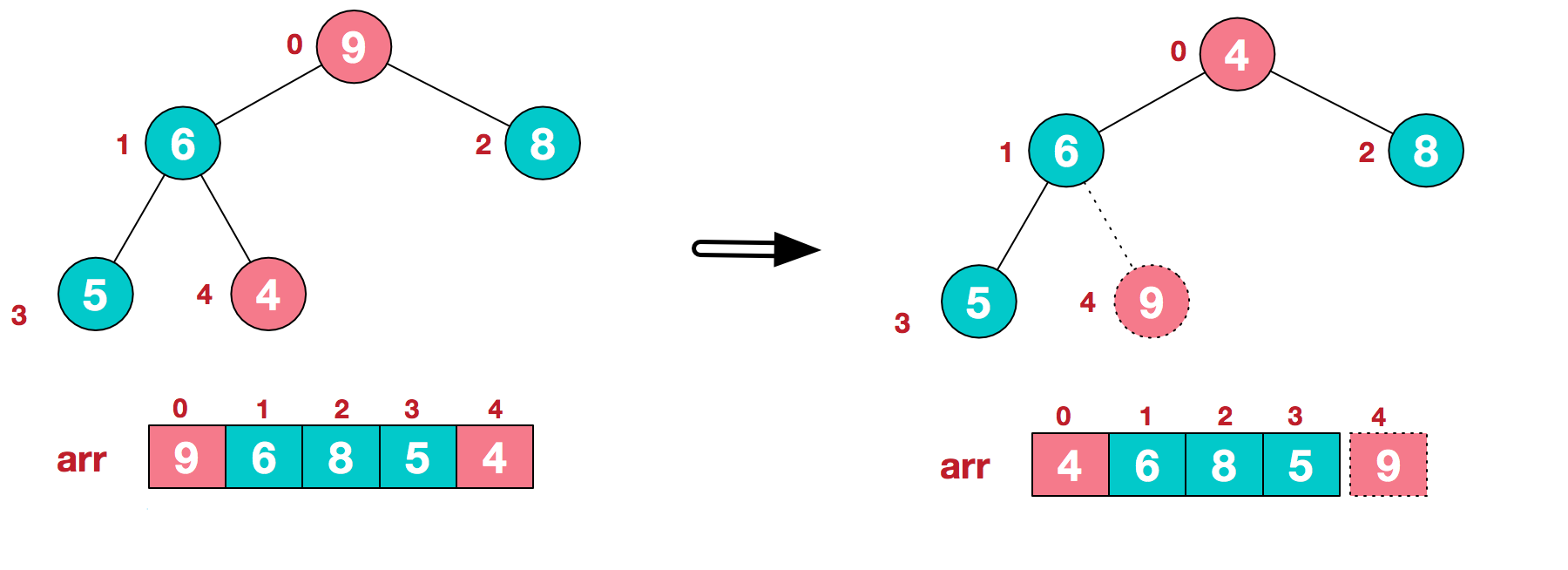
六、使用堆:堆排序
- a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
- b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
- c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
- 例如

教材学习中的问题和解决过程
- 问题1:对于优先队列的定义不太理解
- 问题1解决方案:
- 书中定义:
优先队列是一个服从两个有序规则的集合。首先,具有更高优先级的项排在前面。其次,具有相同优先级的项按先进先出的规则排列。
-
个人对于优先队列定义的理解:
- 优先队列,顾名思义,首先它是一个队列,但是它强调了“优先”二字,所以,已经不能算是一般意义上的队列了,它的“优先”意指取队首元素时,有一定的选择性,即根据元素的属性选择某一项值最优的出队。在生活中,优先队列的例子挺常见的,比如在排队乘电梯时,老师优先上电梯,同学们按照排队的顺序乘梯。
-
问题2:优先队列与堆有什么关系?
-
问题2解决方案:
- 优先队列的实现可以用多个队列来实现,具有相同优先级的项保存在一个队列中。但是,由于堆的“每个元素都要大于或小于它的所有孩子”的特性,并且堆排序是“先将一组元素一项一项插入到堆中,然后一次删除一个”,因此可以利用堆来实现优先队列。
代码调试中的问题和解决过程
- 问题1:在单步跟踪LinkedMaxHeap的过程中,有个add方法:
public void addElement(T obj) {
HeapNode<T> node = new HeapNode<T>(obj);
if (root == null)
root = node;
else {
HeapNode<T> nextParent = getNextParentAdd();
if (nextParent.getLeft() == null)
nextParent.setLeft(node);
else
nextParent.setRight(node);
node.setParent(nextParent);
}
lastNode = node;
modCount++;
if (size() > 1)
heapifyAdd();
}
其中有段代码: node.setParent(nextParent); 在add方法中已经明确表明nextParent.setLeft(node);
那设置node结点的父节点是newParent有什么意义?
- 问题1解决方案:解决这个问题要结合HeapNode的代码。在HeapNode的代码中有个HeapNode的变量parent,在里面的很多方法里面,都有用到这个变量,书上也有说:“有到父节点的引用,这样就可以沿树中的路径移动。”因此setParent方法是在堆中必要的
代码托管
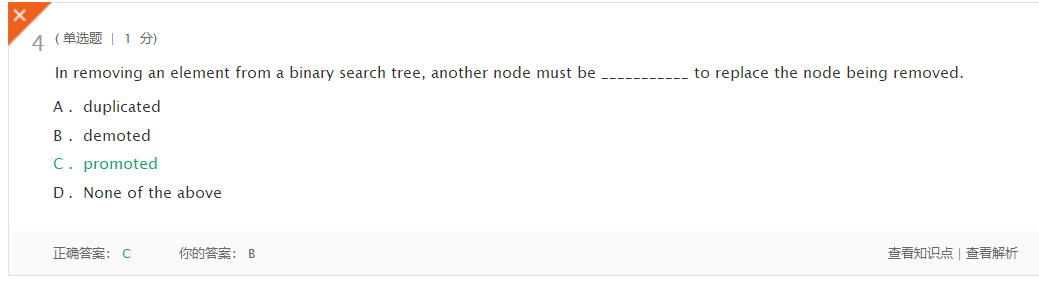
上周考试错题总结
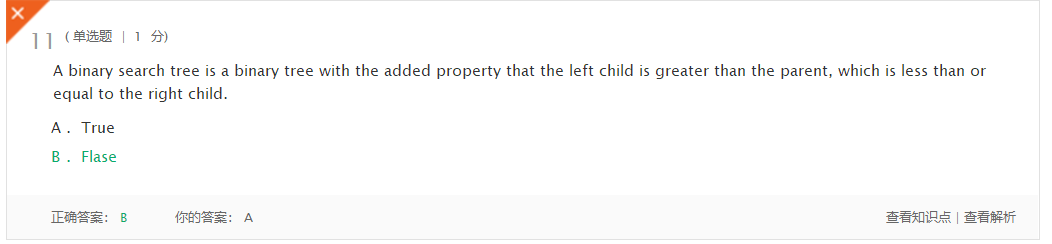
- 当时看书没认真看,不知道怎么想的就选错了
- 记错了,隐约记得一个选项见过,结果记混了

- 看题不认真,没注意到题写的左孩子小于
结对及互评
- 本周结对学习情况
- 结对学习内容
- 认真学习了十二章的内容
- 讨论了堆的添加和删除等操作
- 研究了蓝墨云作业
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | |
|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 |
| 第一周 | 0/0 | 1/1 | 8/8 |
| 第二周 | 671/671 | 1/2 | 17/25 |
| 第三周 | 345/1016 | 1/3 | 15/40 |
| 第四周 | 405/1421 | 2/5 | 23/63 |
| 第五周 | 1202/2623 | 1/5 | 20/83 |
| 第六周 | 1741/4364 | 1/6 | 20/103 |
| 第七周 | 400/4764 | 1/7 | 20/123 |
| 第八周 | 521/5285 | 2/9 | 24/147 |


