20172321 《程序设计与数据结构》第一周学习总结

20172321 《程序设计与数据结构》第一周学习总结

教材学习内容总结

第一章 概述

1.1 软件质量

• 软件工程是一门关于高质量软件开发的技术和理论的学科。
• 高质量软件的特征

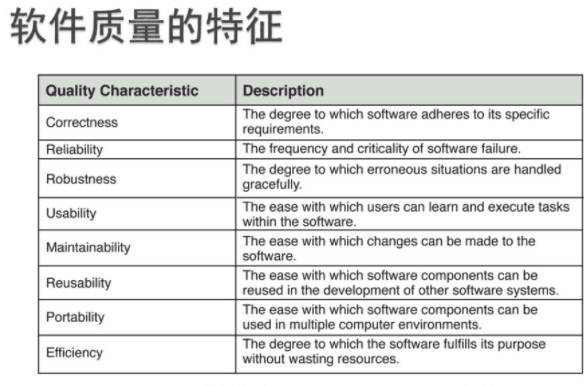
1.2 数据结构

• 数据结构是计算机存储、组织数据的方式。
• 数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。
• 常用结构

第二章

2.1 算法效率分析

• 算法效率通常用CPU的使用时间表示
• 算法分析是从效率的角度对算法进行分类

2.2 增长函数与大O记法

• 增长函数表示与该问题大小相对应的时间或者空间的使用。该函数表示了该算法的事件复杂度或空间复杂度。
• 渐进复杂度称为算法的阶次。主要关注随着问题大小的增加时增长函数的一般性质，这一性质取决于该表达式的主项，即n增加时表达式中增长最快的那一项。
• 大O记法

2.3 增长函数的比较

• 处理器提速10倍后能处理的问题大小的增加倍速

• n相对较小时

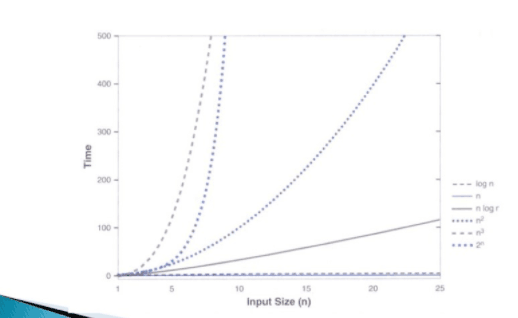
• n很大时

2.4 时间复杂度分析

• 循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数

for (int count = 0; count < n; count++)
{
  // 复杂度为O(1)的步骤系列
}     

• 分析嵌套循环的复杂度时，必须将内层循环和外层循环都考虑进来

for (int count = 0; count < n; count++)
    for (int count2 = 0; count2 < n; count2++)
    {
        //复杂度为O(1)步骤系列
    }

教材学习中的问题和解决过程

问题：书上第15页说，在算法复杂度中使用对数时，基本上是指以2为底的对数，那么特殊情况一般出现在什么时候呢。
解答：其实我主要是想知道特殊情况之后剩下的都是基本情况了。

教材习题作答

• EX2.1 下列增长函数的阶次是多少？

  • a.10n^2+100n+1000
  • 解：O(n^2)
  • b.10n^3-7
  • 解：O(n^3)
  • c.2ⁿ⁺¹⁰⁰ⁿ3
  • 解：O(2^n)
  • d.n^2 ·logn
  • 解：O(n^2 ·logn)
  • 这道题和书上图2.2的例题基本一样。

• EX2.4 请确定下面代码段的增长函数和阶次：

  for(int count = 0 ; count < n ; count++)
      for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
      {
          System.out.println(count,count2);
      }
  }
  

  • 解：这段代码可以看出是嵌套循环，内层循环的循环次数是n/2，外层循环的循环次数是n，所以增长函数为：F(n)=(n^{2)/2，所以阶次为O(n}2)。

• EX 2.5：请确定下面代码段的增长函数和阶次:

  for(int count = 0 ; count < n ; count++)
      for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
      {
          System.out.println(count,count2);
      }
  }
  

  • 解：这段代码可以看出是嵌套循环，内层循环的循环次数是logn，外层循环的循环次数是n，所以增长函数为：F(n)=nlogn，所以阶次为O(nlogn)。

结对及互评

其他（感悟、思考等，可选）

按照这么多年以来的惯例，每到学期之初，我就应该在此立下誓言：这个学期开始我要好好学习、天天向上，多读书，多看报，少吃零食，多睡觉。

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	0/0	1/1	8/8

参考资料

• [Java软件结构与数据结构]（第四版）
• java中的各个数据结构区别