计算方法 | 方程组求解的三角分解

有两种方法，一个是通过高斯消去法的方式去求一个下三角矩阵，还有一个是直接分解。

显然直接分解好啊233。

然后这是个啥杜尔利特分解公式。

是由矩阵乘法的原理弄出来的。

书上P99页俩公式(5.34 5.35)。

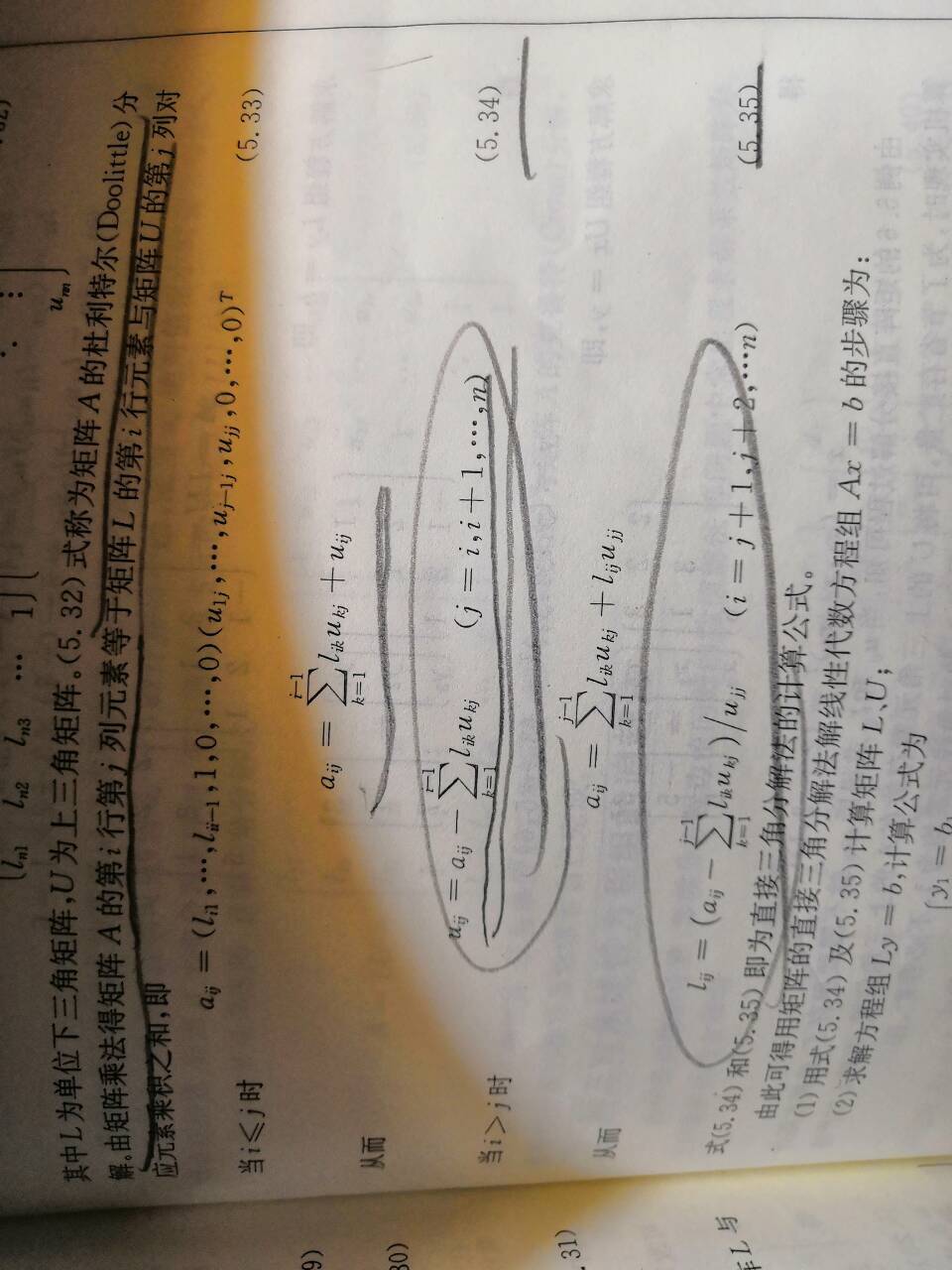
轮流求u和l

三角分解部分的代码：

 1 import numpy as np
 2 
 3 mat = [[2,2,3],[4,7,7],[-2,4,5]]
 4 
 5 height = len(mat)
 6 width = len(mat[0])
 7 
 8 # 1 直接分解矩阵
 9 # 初始化LU
10 U = [[0 for i in range(width)] for j in range(height)]
11 L = [[0 if i!=j else 1 for i in range(width) ] for j in range(height)]
12 
13 print(L,U)
14 
15 # 从U第一行开始，对于L来说是从第一列开始
16 for i in range(height):
17     # 依次计算LU的行、列
18     for j in range(i, width):
19         _sum = 0
20         for k in range(i):
21             _sum += L[i][k] * U[k][j]
22             print("U{}{}_sum += L[{}][{}] * U[{}][{}] = {} * {} = {}".format(i,j,i,k,k,j,L[i][k],U[k][j],L[i][k] * U[k][j]))
23         U[i][j] = mat[i][j] - _sum
24     # L的i.j是反着的
25     for j in range(i, width):
26         _sum = 0
27         if j > i:
28             for k in range(i):
29                 _sum += L[j][k] * U[k][i]
30                 print("L{}{}_sum += L[{}][{}] * U[{}][{}] = {} * {} = {}".format(j,i,j,k,k,i,L[j][k],U[k][i],L[j][k] * U[k][i]))
31             L[j][i] = (mat[j][i] - _sum) / U[i][i]
32     print("L = \n{}".format(np.array(L)))
33     print("U = \n{}".format(np.array(U)))
34     
35 # 分解完毕

解Ly =b, 回带求解，再解Ux=y, 直接丢完整代码了：

 1 import numpy as np
 2 # mat = eval(input("请输入系数矩阵："))
 3 # 测试数据[[2,2,3],[4,7,7],[-2,4,5]]
 4 mat = [[2,2,3],[4,7,7],[-2,4,5]]
 5 # b = eval(input("请输入结果矩阵:"))
 6 # 测试数据[[3],[1],[-7]]
 7 b = [[3],[1],[-7]]
 8 height = len(mat)
 9 width = len(mat[0])
10 
11 # 1 直接分解矩阵
12 # 初始化LU
13 U = [[0 for i in range(width)] for j in range(height)]
14 L = [[0 if i!=j else 1 for i in range(width) ] for j in range(height)]
15 
16 print(L,U)
17 
18 # 从U第一行开始，对于L来说是从第一列开始
19 for i in range(height):
20     # 依次计算LU的行、列
21     for j in range(i, width):
22         _sum = 0
23         for k in range(i):
24             _sum += L[i][k] * U[k][j]
25             print("U{}{}_sum += L[{}][{}] * U[{}][{}] = {} * {} = {}".format(i,j,i,k,k,j,L[i][k],U[k][j],L[i][k] * U[k][j]))
26         U[i][j] = mat[i][j] - _sum
27     # L的i.j是反着的
28     for j in range(i, width):
29         _sum = 0
30         if j > i:
31             for k in range(i):
32                 _sum += L[j][k] * U[k][i]
33                 print("L{}{}_sum += L[{}][{}] * U[{}][{}] = {} * {} = {}".format(j,i,j,k,k,i,L[j][k],U[k][i],L[j][k] * U[k][i]))
34             L[j][i] = (mat[j][i] - _sum) / U[i][i]
35     print("L = \n{}".format(np.array(L)))
36     print("U = \n{}".format(np.array(U)))
37     
38 print("分解完毕，开始计算Ly=b")
39 # 分解完毕 解Ly =b
40 y = [[0] for i in range(height)]
41 # print(y)
42 for i in range(height):
43     _sum = 0
44     for k in range(i):
45         _sum += L[i][k] * y[k][0]
46     y[i][0] = (b[i][0] - _sum)          # 这里不用除以系数因为对角线为1
47     print(y)
48 print("计算完毕，开始计算Ux=y")
49 x = [[0] for i in range(height)]
50 for i in range(height-1,-1,-1):
51     _sum = 0
52     for k in range(height-1,i,-1):
53         _sum += U[i][k] * x[k][0]
54     x[i][0] = (y[i][0] - _sum) / U[i][i]
55     print(x)
56 print("最终结果x: \n{}".format(np.array(x)))

over。

 

posted @ 2020-10-21 15:34  Mz1  阅读(176)  评论(0)  编辑  收藏  举报