CF1102(*^▽^*)
A.Integer Sequence Dividing
题目大意：
给出\(n\)，要求把序列\(1,2,…,n\)分成两个集合，输出两个集合的和的最小差值。\((1\leqslant n\leqslant 2\times 10^{9})\)
解题思路：
我们坚信它是可以分成我们想要的两个差值最小的集合的 差值一定和\(\Sigma_{i=1}^{n}i\)有关。若\(\Sigma_{i=1}^{n}i\)是偶数，那么差值为零，否则必为一。
详细一点：为了抵消差值，分集合时一定是\(1,n\)一组、\(2,n-1\)一组……以此类推。那么有以下几种情况：
- 全部抵消完，差值一定为零。
- 剩下一个数，我们将 \(1\) 提出来，将剩下的 \(n-1\) 个数按照以上方式匹配，最开始的 \(1\) 即是差值。
- 剩下两个数，将 \(1,2\) 提出来，剩下的继续分，最后差值即为 \(2-1\) 也就是 \(1\) 。
- 剩下三个数，将 \(1,2,3\) 提出来，剩下的继续分，最后差值即为 \(1+2-3\) 也就是 \(0\) 。
- 剩下四个数？是不会剩下四个数的
综上，差值不是 \(0\) 就是 \(1\) 。那么显然，答案就和\(\Sigma ^{n}_{i=1}i\)的奇偶有关了。
真·小代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
int n;
signed main()
{
scanf("%lld",&n);
int sum=(n+1)*n/2;
printf("%lld",sum%2);
return 0;
}
B.Array K-Coloring
题目大意：
给出一个长度为\(n\)的序列\(a\)，用\(k\)种颜色染色，要求：
- 每种颜色必须用到
- 每个元素必须被染色
- 序列中相同的数字不能染上相同的颜色，即对于\(a_{i}=a_{j},i\neq j\)，满足\(col_{i}\neq col_{j}\)
若可行，则输出染色方案。\((1\leqslant k\leqslant n\leqslant 5000)\)
解题思路：
满足第一个要求，只需要从 \(1\)~\(k\) 反复给序列染色，每次++，超过\(k\)就归一；满足第三个要求，那么先给序列\(a\)排序，使相同的\(a_{i}\)在同一区间内被染色（根据染色方法，相邻两个元素不会染同样的色）。根据鸽巢原理，若元素\(a_{i}\)的数量超过\(k\)，那么一定无法染色
不好的代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=5005;
int n,k;
struct node{
int x,d,col;
}a[N];
int p;
bool cmp1(node x,node y) { return x.x<y.x; }
bool cmp2(node x,node y) { return x.d<y.d; }
signed main()
{
scanf("%lld%lld",&n,&k);
for (int i=1;i<=n;i++)
{
scanf("%lld",&a[i].x);
a[i].d=i;
}
sort(a+1,a+1+n,cmp1);
p=1;//颜色指针
int cnt=1;//记录相同元素的个数
for (int i=1;i<=n;i++)
{
if (a[i].x==a[i-1].x) cnt++;
else cnt=1;
if (cnt>k) { printf("NO"); return 0; }
a[i].col=p++;
if (p>k) p=1;
}
sort(a+1,a+1+n,cmp2);
printf("YES\n");
for (int i=1;i<=n;i++) printf("%lld ",a[i].col);
return 0;
}
C.Doors Break and Repairing
题目大意：
给定一个长度为\(n\)的数列\(a\)，以下两个操作交替进行：
- 选择一个\(a_{i}\neq0\)，使得\(a_{i}=max(a_{i}-x\ ,\ 0\ )\)
- 选择一个\(a_{i}\neq0\)，使得\(a_{i}=a_{i}+y\)。
执行操作一的一方想要尽可能地使更多地\(a_{i}\)变成 \(0\)，执行操作二的一方想要尽可能地让更少的\(a_{i}\)变成 \(0\)。求双方都采取最优策略时，最多有多少个\(a_{i}\)为 \(0\)。\((1\leqslant n\leqslant 100,1\leqslant x,y,a_{i}\leqslant 10^{5})\)
解题思路：
对\(x,y\)的关系进行分类讨论。
- 若\(x>y\)，由于没有操作次数的限制，所以最后序列中所有数一定会归零（感性理解为入不敷出迟早要没）
- 若\(x\leqslant y\)，那么只有\(a_{i}\leqslant x\)才有可能被清零（感性理解为一次pass掉）；又因操作二采取最优策略，每次一定会选择\(a_{i}\leqslant x\)进行操作，而操作完毕后\(a_{i}\)一定无法被一次清零；所以记\(cnt\)为原序列中\(a_{i}\leqslant x\)的个数，最后序列中会有\(\lceil \frac{cnt}{2}\rceil\)个数归零。
小代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=110;
int n,x,y;
int a[N];
int cnt;
signed main()
{
scanf("%lld%lld%lld",&n,&x,&y);
for (int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
if (a[i]<=x) cnt++;
}
if (x>y) printf("%lld",n);
else printf("%lld",(cnt+1)/2);
return 0;
}
D.Balanced Ternary String
题目大意：
给出一个长度为\(n\)、仅由'\(0\)','\(1\)','\(2\)'组成的字符串\(s\)，要求改动最少的位置，使得\(s\)中\(0,1,2\)的个数相同；若有多种方案，输出字典序最小的一个。\((\)保证\(n\)是\(3\)的倍数，\(3\leqslant n\leqslant 3\times 10^{5})\)
解题思路：
显然贪心。若需要改动，一定要让\(0\)尽量靠前，\(2\)尽量靠后，\(1\)最后考虑。
然后直接模拟就行了？
！代码很史，谨慎查看！
！代码很史，谨慎查看！
！代码很史，谨慎查看！
很史的代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+5;
const int inf=0x3f3f3f3f3f3f3f3f;
int n;
char s[N];
int num;
int bx[3];//每个字符出现的个数
vector <int> d[3];
int l[3],r[3];//指针，指向改动的最前、最后位置
signed main()
{
scanf("%lld%s",&n,s);
num=n/3;
for (int i=0;i<n;i++)
{
bx[(int)(s[i]-'0')]++;
d[(int)(s[i]-'0')].push_back(i);
}
r[0]=bx[0]-1,r[1]=bx[1]-1,r[2]=bx[2]-1;
while (bx[0]<num)
{
int mn=inf;//0尽量靠前
if (bx[1]>num) mn=min(mn,d[1][l[1]]);
if (bx[2]>num) mn=min(mn,d[2][l[2]]);
bx[0]++;
s[mn]='0';
if (bx[1]>num&&mn==d[1][l[1]]) l[1]++,bx[1]--;
else l[2]++,bx[2]--;
}
while (bx[2]<num)
{
int mx=0;//2尽量靠后
if (bx[1]>num) mx=max(mx,d[1][r[1]]);
if (bx[0]>num) mx=max(mx,d[0][r[0]]);
bx[2]++;
s[mx]='2';
if (bx[1]>num&&mx==d[1][r[1]]) r[1]--,bx[1]--;
else r[0]--,bx[0]--;
}
while (bx[1]<num)
{
int dd;
if (bx[0]>num) dd=d[0][r[0]];//1最后看情况
else dd=d[2][l[2]];
bx[1]++;
s[dd]='1';
if (bx[0]>num) r[0]--,bx[0]--;
else l[2]++,bx[2]--;
}
printf("%s",s);
return 0;
//都看到这了，为蒟蒻的代码提提建议吧，总感觉这样写太废太冗杂了……
}
E.Monotonic Renumeration
题目大意：
给出一个长度为\(n\)的序列\(a\)，需构造一个单调不降的序列\(b\)，满足：
- \(b_{1}=0\)
- 对于\(i\in [2,n]\)，\(b_{i}=b_{i-1}\)或\(b_{i}=b_{i-1}+1\)
- 对于任意一组\(i,j\)，若满足\(a_{i}=a_{j}\)，那么必须\(b_{i}=b_{j}\)
要求输出构造\(b\)序列的方案数，对\(998244353\)取模\((2\leqslant n\leqslant 2\times10^{5},1\leqslant a_{i}\leqslant 10^{9})\)
解题思路：
小清新计数题。
注意到条件三的限制，我们手模后发现对于满足\(a_{i}=a_{j}\)的区间\([i,j]\)，应也满足\(b_{i}=b_{i+1}=…=b_{j}\)，不然无法保证\(b\)序列单调不降。序列\(a\)中会形成若干个以上描述的区间，若几个区间内有交，那么可以看作一个大区间（虽然大区间的两个端点\(i,j\)可能不满足\(a_{i}=a_{j}\)，但仍需满足大区间内\(b\)中元素相等）。
对于大区间\([i,j]\)，必然满足\(b_{i}=b_{i+1}=…=b_{j}\)。对于每个大区间\(i\)，它有两种取值；于是统计大区间的个数\(cnt\)，方案数就是\(2^{cnt-1}\)。（因为第一个区间，也就是\(b_{1}\)所在的区间取值是确定的）
可结合图片食用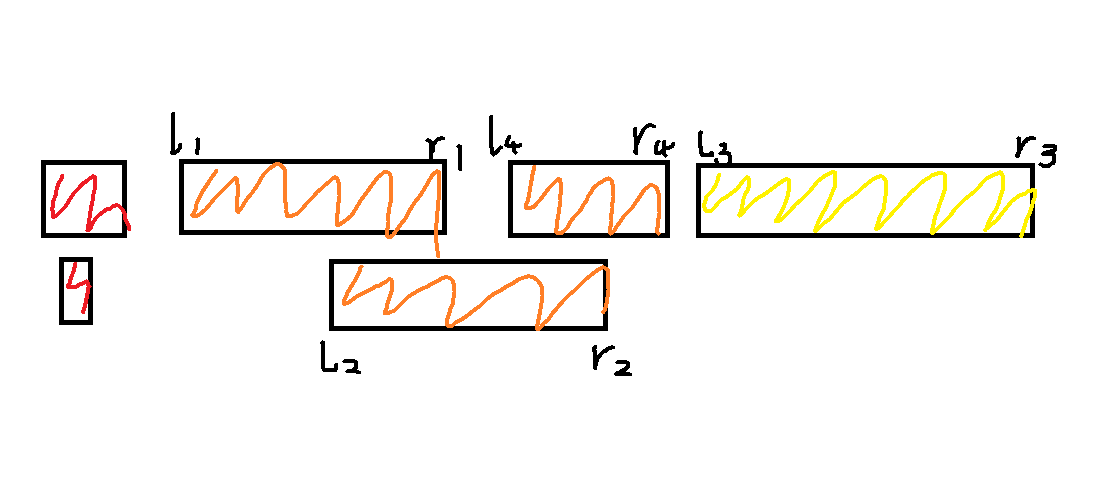
um有点难评……那么，结合代码食用
可爱的小代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
const int MOD=998244353;
int n;
int a[N];
map <int,int> mx,mn;//可恶的数据范围 不能用数组存
int tol;
struct node{
int l,r;//记录对于相同元素a[i]所形成的最大区间
}st[N];
bool cmp(node x,node y) { return x.l<y.l; }
int qsm(int a,int b)//注意到数据范围，选择快速幂
{
int res=1;
while (b)
{
if (b&1) res=(res*a)%MOD;
a=(a*a)%MOD;
b>>=1;
}
return res;
}
signed main()
{
scanf("%lld",&n);
for (int i=1;i<=n;i++) scanf("%lld",&a[i]);
for (int i=1;i<=n;i++) mx[a[i]]=i;//统计每个数出现的最初、最后位置
for (int i=n;i>=1;i--) mn[a[i]]=i;
for (int i=1;i<=n;i++) st[i]={mn[a[i]],mx[a[i]]};//记录a[i]所在的第一种区间
sort(st+1,st+1+n,cmp);
int r=st[1].r;
for (int i=2;i<=n;i++)//统计不交区间个数
{
if (st[i].l>r) tol++;
r=max(r,st[i].r);
}
printf("%lld",qsm(2,tol));
return 0;
}
F.Elongated Matrix
题目大意：
给定一个\(n\)行\(m\)列的矩阵\(a_{i,j}\)，你可以改变每一行的顺序，但不能改变行内元素的位置。
确定矩形后，你可以通过以下顺序遍历整个矩阵：首先从顶部到底部遍历矩阵第一列，然后对第二列进行相同操作，以此类推。在遍历期间，按照遍历顺序记录序列\(s\)，记为\(s_{1},s_{2},s_{3},…,s_{nm}\)
我们称一个\(k\)是合法的，当且仅当对于\(\forall i\in [2,nm]\)，满足\(|s_{i}-s_{i-1}|\geqslant k\)。
要求对于给出矩阵，合法的\(k\)值最大。\((1\leqslant n\leqslant 16,1\leqslant m\leqslant 10^{4},2\leqslant nm)\)
解题思路：
看到数据范围，果断想到状压dp 但是我还是不会QwQ
注意到时限为4s。嗯4s。4s？4s！
设状态\(f_{i,j}\)表示已选了\(i\)集合的行、以\(j\)行结尾的最大\(k\)值。状态转移方程即
其中\(g_{i,j}\)表示第\(i,j\)行相邻时的最小差值，暂时不考虑第一行与最后一行的差值
那么统计答案时，因为最后一行不确定，所以枚举最后一行的位置统计，即
其中\(h_{k,i}\)表示第\(k\)行作为第一行、第\(i\)行作为最后一行时两行的最小差值。
复杂度\(O(2^{n}n^{3})\)
不做评价的代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=20;
const int M=1e4+5;
const int inf=0x3f3f3f3f3f3f3f3f;
int n,m;
int a[N][M];
int f[1<<N][N],g[N][N],h[N][N];
int ans;
signed main()
{
scanf("%lld%lld",&n,&m);
for (int i=0;i<n;i++)
{
for (int j=1;j<=m;j++) scanf("%lld",&a[i][j]);
}
//预处理
for (int i=0;i<n;i++)//i,j分别枚举行
{
for (int j=0;j<n;j++)
{
g[i][j]=h[i][j]=inf;
for (int k=1;k<=m;k++) g[i][j]=min(g[i][j],abs(a[i][k]-a[j][k]));//枚举第二维坐标
for (int k=2;k<=m;k++) h[i][j]=min(h[i][j],abs(a[i][k-1]-a[j][k]));
}
}
for (int k=0;k<n;k++)//枚举第一行
{
memset(f,0,sizeof f);
f[1<<k][k]=inf;
for (int s=0;s<(1<<n);s++)//枚举行的集合
{
for (int i=0;i<n;i++)
{
if (!(s&(1<<i))) continue;
for (int j=0;j<n;j++)
{
if (!(s&(1<<j))) f[s|(1<<j)][j]=max(f[s|(1<<j)][j],min(f[s][i],g[i][j]));
}
}
}
for (int i=0;i<n;i++) ans=max(ans,min(f[(1<<n)-1][i],h[k][i]));//枚举最后一行并统计答案
}
printf("%lld",ans);
return 0;
}
完结撒花
