BZOJ3672 [Noi2014]购票 【点分治 + 斜率优化】

题目链接

BZOJ3672

题解

如果暂时不管\(l[i]\)的限制，并假使这是一条链
设\(f[i]\)表示\(i\)节点的最优答案，我们容易得到\(dp\)方程

\[f[i] = min\{f[j] + (d[i] - d[j])p[i] + q[i]\} \]

显而易见可以斜率优化
化为

\[f[j] = p[i]d[j] + f[i] \]

那么决策点就是\((d[j],f[j])\)，决策就是用斜率为\(p[i]\)的直线截得最小截距
显然维护下凸包即可，而且\(d[j]\)单调，可以逐点加入

好了以上就是直线上不带\(l[i]\)限制的口胡
如果强行搬到树上来，可以使用可持久化数组维护
但是加上\(l[i]\)的限制，仍然强行截出\(l[i]\)之后的点，是不对的
如图：

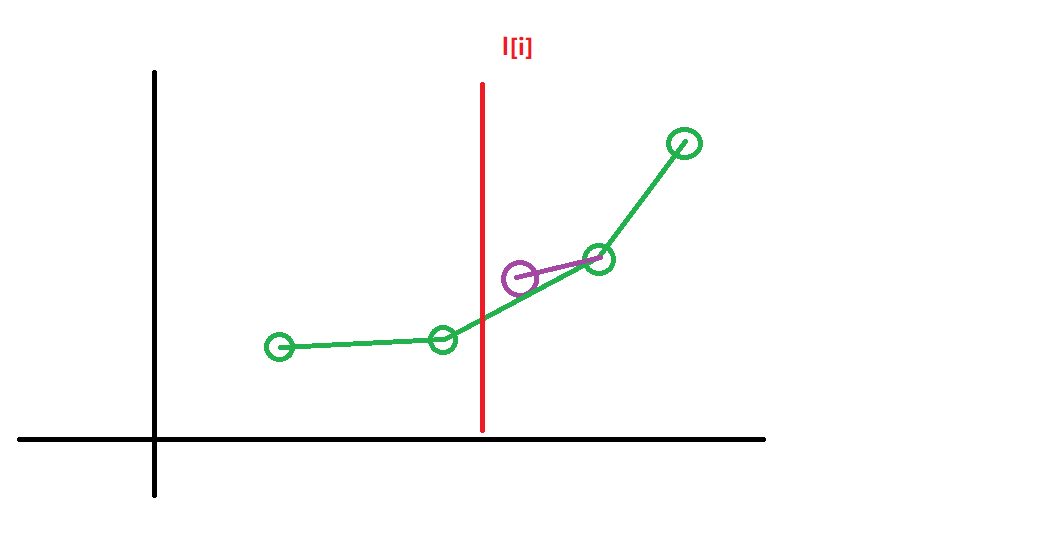
图中紫色点在过程中被出栈了，截掉\(l[i]\)之前的点之后，并不会在凸包中，而实际应被考虑进来

所以就要使用点分治 + 斜率优化的黑科技了OvO
1、我们先分治一棵以\(u\)为根子树，如果子树大小为\(1\)直接返回
2、寻找到这棵树的重心，先将重心\(rt\)的儿子打个标记堵上
3、然后再分治以\(u\)为根的子树
4、分治完后，显然\(rt\)节点及以上的节点的\(f[i]\)都更新完毕，我们使用\(u\)到\(rt\)路径上所有点来更新子树内的\(f[i]\)
5、将\(rt\)子树内的点拿出来，按\(d[i] - l[i]\)——即最高能对其进行更新的位置——降序排序
6、将\(rt\)及以上节点逐一在可以进行更新时加入凸包，子树内的点在凸包上二分更新答案
7、分治各个子树

树分治是\(O(nlogn)\)的，分治过程中子树内每一个节点都要进行一次二分，所以总复杂度是\(O(nlog^2n)\)

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define mp(a,b) make_pair<int,int>(a,b)
#define cls(s) memset(s,0,sizeof(s))
#define cp pair<int,int>
#define LL long long int
using namespace std;
const int maxn = 200005,maxm = 10000005,oo = 1000000000;
const LL INF = 1000000000ll * 1000000001ll;
inline LL read(){
	LL out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
int n,fa[maxn],Ls[maxn],Rb[maxn];
LL p[maxn],q[maxn],f[maxn],L[maxn],d[maxn],s[maxn];
int F[maxn],sz[maxn],rt,vis[maxn];
void getrt(int u,int Siz){
	sz[u] = 1; F[u] = 0;
	for (int k = Ls[u]; k; k = Rb[k])
		if (!vis[k]){
			getrt(k,Siz); sz[u] += sz[k]; F[u] = max(F[u],sz[k]);
		}
	F[u] = max(F[u],Siz - sz[u]);
	if (F[u] <= F[rt]) rt = u;
}
int c[maxn],ci;
void dfs(int u){
	c[++ci] = u;
	for (int k = Ls[u]; k; k = Rb[k]) if (!vis[k]) dfs(k);
}
inline bool cmp(const int& a,const int& b){
	return d[a] - L[a] > d[b] - L[b];
}
int st[maxn],top;
double sl[maxn];
double slope(int u,int v){
	return (double)(f[u] - f[v]) / (double)(d[u] - d[v]);
}
void ins(int u){
	while (top > 1 && slope(u,st[top]) >= sl[top - 1])
		top--;		
	st[++top] = u;
	if (top > 1) sl[top - 1] = slope(st[top],st[top - 1]);
	sl[top] = -INF;
}
LL query(int u){
	int l = 1,r = top,mid;
	while (l < r){
		mid = l + r>> 1;
		if (sl[mid] <= p[u]) r = mid;
		else l = mid + 1;
	}
	return f[st[l]] + (d[u] - d[st[l]]) * p[u] + q[u];
}
void solve(int u,int Siz){
	if (Siz == 1) return;
	F[rt = 0] = oo; getrt(u,Siz); int x = rt;
	for (int k = Ls[x]; k; k = Rb[k]) vis[k] = true,Siz -= sz[k];
	solve(u,Siz);
	ci = 0; for (int k = Ls[x]; k; k = Rb[k]) dfs(k);
	sort(c + 1,c + 1 + ci,cmp);
	int now = x; top = 0;
	for (int i = 1; i <= ci; i++){
		int v = c[i];
		while (now != fa[u] && d[v] - L[v] <= d[now]) ins(now),now = fa[now];
		if (top) f[v] = min(f[v],query(v));
	}
	for (int k = Ls[x]; k; k = Rb[k]) solve(k,sz[k]);
}
int main(){
	n = read(); read();
	for (int i = 2; i <= n; i++){
		fa[i] = read(); s[i] = read(); d[i] = d[fa[i]] + s[i];
		p[i] = read(); q[i] = read(); L[i] = read();
		Rb[i] = Ls[fa[i]]; Ls[fa[i]] = i;
		f[i] = INF;
	}
	solve(1,n);
	for (int i = 2; i <= n; i++) printf("%lld\n",f[i]);
	return 0;
}