BZOJ3884 上帝与集合的正确用法 【欧拉定理】

题目

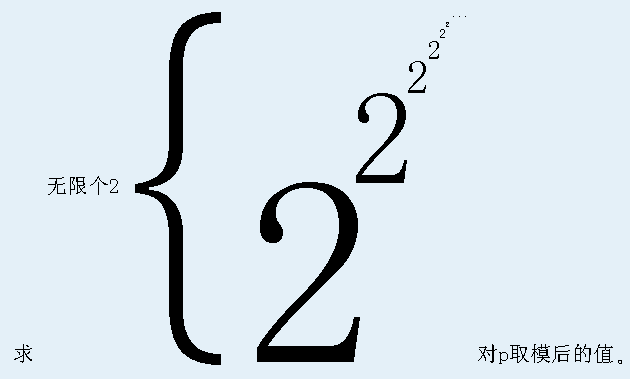
对于100%的数据，T<=1000,p<=10^7

题解

来捉这道神题

欧拉定理的一般形式：

\[a^{m} \equiv a^{m \mod \varphi(p) + [m \ge \varphi(p)]\varphi(p)} \pmod p \]

我们令

\[ans(p) = 2^{2^{2^{...}}} \mod p \]

那么有

\[ans(p) = 2^{ans(\varphi(p)) + \varphi(p)} \mod p \]

\(O(\log p)\)递归即可

#include<iostream>
#include<cstdio>
#include<cmath>
#include<bitset>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");
using namespace std;
const int maxn = 10000005,maxm = 100005,INF = 1000000000;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
bitset<maxn> isn;
int p[maxn],phi[maxn],pi;
void init(){
	phi[1] = 1;
	for (int i = 2; i <= 10000000; i++){
		if (!isn[i]) p[++pi] = i,phi[i] = i - 1;
		for (int j = 1; j <= pi && i * p[j] <= 10000000; j++){
			isn[i * p[j]] = true;
			if (i % p[j] == 0){
				phi[i * p[j]] = phi[i] * p[j];
				break;
			}
			phi[i * p[j]] = phi[i] * (p[j] - 1);
		}
	}
}
int qpow(int a,int b,int p){
	int ans = 1;
	for (; b; b >>= 1,a = 1ll * a * a % p)
		if (b & 1) ans = 1ll * ans * a % p;
	return ans;
}
int Ans(int p){
	if (p == 1) return 0;
	return qpow(2,Ans(phi[p]) + phi[p],p);
}
int main(){
	init();
	int T = read(),p;
	while (T--){
		p = read();
		printf("%d\n",Ans(p));
	}
	return 0;
}