NOI2015 荷马史诗 【k-哈夫曼树】
题目
追逐影子的人,自己就是影子 ——荷马
Allison 最近迷上了文学。她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》 组成的鸿篇巨制《荷马史诗》实在是太长了,Allison 想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有n种不同的单词,从1到n进行编号。其中第i种单 词出现的总次数为wi。Allison 想要用k进制串si来替换第i种单词,使得其满足如下要求:
对于任意的 1 ≤ i, j ≤ n , i ≠ j ,都有:si不是sj的前缀。
现在 Allison 想要知道,如何选择si,才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下,Allison 还想知道最长的si的最短长度是多少?
一个字符串被称为k进制字符串,当且仅当它的每个字符是 0 到 k − 1 之间(包括 0 和 k − 1 )的整数。
字符串 str1 被称为字符串 str2 的前缀,当且仅当:存在 1 ≤ t ≤ m ,使得str1 = str2[1..t]。其中,m是字符串str2的长度,str2[1..t] 表示str2的前t个字符组成的字符串。
输入格式
输入的第 1 行包含 2 个正整数 n, k ,中间用单个空格隔开,表示共有 n种单词,需要使用k进制字符串进行替换。
接下来n行,第 i + 1 行包含 1 个非负整数wi ,表示第 i 种单词的出现次数。
输出格式
输出包括 2 行。
第 1 行输出 1 个整数,为《荷马史诗》经过重新编码以后的最短长度。
第 2 行输出 1 个整数,为保证最短总长度的情况下,最长字符串 si 的最短长度。
输入样例
4 2
1
1
2
2
输出样例
12
2
提示
【样例说明 1】
用 X(k) 表示 X 是以 k 进制表示的字符串。
一种最优方案:令 00(2) 替换第 1 种单词, 01(2) 替换第 2 种单词, 10(2) 替换第 3 种单词,11(2) 替换第 4 种单词。在这种方案下,编码以后的最短长度为:
1 × 2 + 1 × 2 + 2 × 2 + 2 × 2 = 12
最长字符串si的长度为 2 。
一种非最优方案:令 000(2) 替换第 1 种单词,001(2) 替换第 2 种单词,01(2)替换第 3 种单词,1(2) 替换第 4 种单词。在这种方案下,编码以后的最短长度为:
1 × 3 + 1 × 3 + 2 × 2 + 2 × 1 = 12
最长字符串 si 的长度为 3 。与最优方案相比,文章的长度相同,但是最长字符串的长度更长一些。
【样例说明 2】
一种最优方案:令 000(3) 替换第 1 种单词,001(3) 替换第 2 种单词,01(3) 替换第 3 种单词, 02(3) 替换第 4 种单词, 1(3) 替换第 5 种单词, 2(3) 替换第 6 种单词。
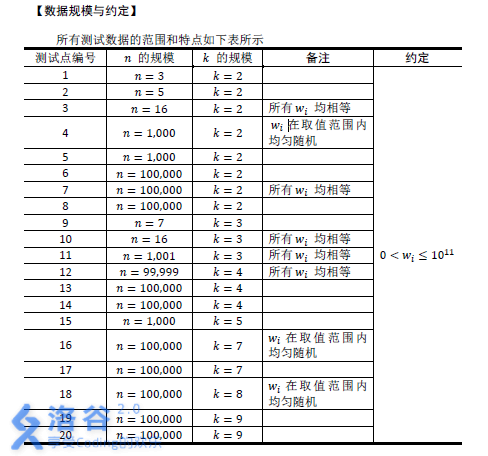
【提示】
选手请注意使用 64 位整数进行输入输出、存储和计算。
【时限1s,内存512M】
题解
当k=2时,就等同于合并果子,每次合并权值最小的两堆
将每次合并的一堆作为父亲,被合并的两堆作为儿子,就会形成一棵树,叫做哈夫曼树
哈夫曼树中所有点到根的距离乘以权值之和最小
通常用于编码,给各种需要的信息附上不同的01串,使得文章最短,当然是出现次数越多的信息赋的01串越短
如果是K进制,就要用上K哈夫曼树,实际上就是每次合并K堆
合并到最后不足K堆怎么办?
每一次合并会减少K - 1堆,所以只要n - 1是k - 1的倍数就可以了,用0补齐
题目还要求最大深度最小,权值相同时深度小的优先即可
#include<iostream>
#include<cstdio>
#include<cmath>
#include<queue>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");
using namespace std;
const int maxn = 100005,maxm = 100005,INF = 1000000000;
inline LL read(){
LL out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
struct node{LL w,d;};
inline bool operator <(const node& a,const node& b){
return a.w == b.w ? a.d > b.d : a.w > b.w;
}
priority_queue<node> q;
int n,k;
int main(){
n = read(); k = read();
REP(i,n) q.push((node){read(),0});
while ((n - 1) % (k - 1) != 0) q.push((node){0,0}),n++;
LL ans = 0,sum,d;
while (n > 1){
sum = 0; d = 0;
for (int i = 1; i <= k; i++) sum += q.top().w,d = max(d,q.top().d),q.pop();
ans += sum;
q.push((node){sum,d + 1});
n -= k - 1;
}
printf("%lld\n%lld\n",ans,q.top().d);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号