BZOJ2555 SubString 【后缀自动机 + LCT】
题目
懒得写背景了，给你一个字符串init，要求你支持两个操作
(1):在当前字符串的后面插入一个字符串
(2):询问字符串s在当前字符串中出现了几次？(作为连续子串)
你必须在线支持这些操作。
输入格式
第一行一个数Q表示操作个数
第二行一个字符串表示初始字符串init
接下来Q行，每行2个字符串Type,Str
Type是ADD的话表示在后面插入字符串。
Type是QUERY的话表示询问某字符串在当前字符串中出现了几次。
为了体现在线操作，你需要维护一个变量mask，初始值为0
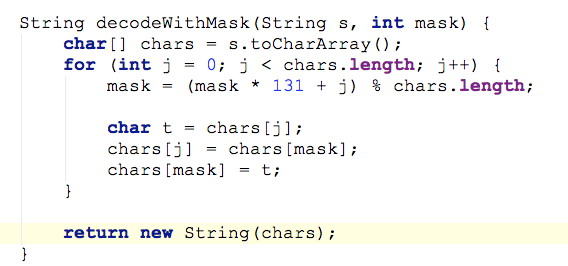
读入串Str之后，使用这个过程将之解码成真正询问的串TrueStr。
询问的时候，对TrueStr询问后输出一行答案Result
然后mask = mask xor Result
插入的时候，将TrueStr插到当前字符串后面即可。
HINT:ADD和QUERY操作的字符串都需要解压
输出格式
输入样例
2
A
QUERY B
ADD BBABBBBAAB
输出样例
0
提示
40 % 的数据字符串最终长度 <= 20000，询问次数<= 1000，询问总长度<= 10000
100 % 的数据字符串最终长度 <= 600000，询问次数<= 10000,询问总长度<= 3000000
新加数据一组--2015.05.20
题解
大码题。。我就知道我会WA【到头来是解压错了= =，注意解压时的mask不是你维护的mask，你维护的mask值在解压前后不应改变】
由后缀自动机的性质，我们给SAM上的点赋值，在主链上的点权为1【即插入的不包括拓展的点】，其它点为0
权值为1的点在parent树上都是叶子节点，而一个节点所形成相同的串的数量就是该节点在parent树中的子树的叶子节点数
那这就好办了，我们用LCT维护parent树，每次加点就将ta到根节点加上ta的权值
由于树根始终不变而且树边有向，我们可以把LCT写得简单一点
【orz hzwer】
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define isr(u) (ch[fa[u]][1] == u)
#define isrt(u) (!fa[u] || (ch[fa[u]][0] != u && ch[fa[u]][1] != u))
#define ls ch[u][0]
#define rs ch[u][1]
using namespace std;
const int maxn = 1200005,maxm = 3000005,INF = 1000000000;
int fa[maxn],tag[maxn],val[maxn],ch[maxn][2];
int pre[maxn],son[maxn][26],step[maxn],cnt,last,n;
char s[maxm];
void add(int u,int v){if (u) val[u] += v,tag[u] += v;}
void pd(int u){
if (tag[u]) add(ls,tag[u]),add(rs,tag[u]),tag[u] = 0;
}
void push_down(int u){
if (!isrt(u)) push_down(fa[u]); pd(u);
}
void spin(int u){
int s = isr(u),f = fa[u];
fa[u] = fa[f]; if (!isrt(f)) ch[fa[f]][isr(f)] = u;
ch[f][s] = ch[u][s ^ 1]; if (ch[u][s ^ 1]) fa[ch[u][s ^ 1]] = f;
fa[f] = u; ch[u][s ^ 1] = f;
}
void splay(int u){
for (push_down(u); !isrt(u); spin(u))
if (!isrt(fa[u])) spin((isr(u) ^ isr(fa[u])) ? u : fa[u]);
}
void Access(int u){
for (int v = 0; u; u = fa[v = u]) splay(u),rs = v;
}
void Cut(int u){
Access(u); splay(u); add(ls,-val[u]);
fa[ls] = 0; ls = 0;
}
void Link(int u,int f){
fa[u] = f; Access(f); splay(f); add(f,val[u]);
}
void ins(int x){
int p = last,np = ++cnt;
last = np; val[np] = 1; step[np] = step[p] + 1;
while (p && !son[p][x]) son[p][x] = np,p = pre[p];
if (!p) pre[np] = 1,Link(np,1);
else {
int q = son[p][x];
if (step[q] == step[p] + 1) pre[np] = q,Link(np,q);
else {
int nq = ++cnt; step[nq] = step[p] + 1;
memcpy(son[nq],son[q],sizeof(son[q]));
pre[nq] = pre[q]; Link(nq,pre[q]);
pre[np] = nq; Link(np,nq);
Cut(q); pre[q] = nq; Link(q,nq);
while (son[p][x] == q) son[p][x] = nq,p = pre[p];
}
}
}
int MASK;
void Mask(int mask){
n = strlen(s);
for (int j = 0; j < n; j++){
mask = (mask * 131 + j) % n;
swap(s[j],s[mask]);
}
}
int solve(){
int u = 1; scanf("%s",s); Mask(MASK);
for (int i = 0; i < n; i++)
if (!(u = son[u][s[i] - 'A'])) return 0;
splay(u);
return val[u];
}
int main(){
int Q,ans; scanf("%d",&Q);
scanf("%s",s);
n = strlen(s); cnt = last = 1;
for (int i = 0; i < n; i++) ins(s[i] - 'A');
while (Q--){
scanf("%s",s);
if (s[0] == 'A'){
scanf("%s",s); Mask(MASK);
for (int i = 0; i < n; i++) ins(s[i] - 'A');
}
else printf("%d\n",ans = solve()),MASK ^= ans;
}
return 0;
}
