K:Treap(堆树)
Treap=Tree+Heap。Treap是一棵二叉排序树,它的左子树和右子树分别是一个Treap,和一般的二叉排序树不同的是, Treap记录一个额外的数据, 就是优先级。Treap在以关键码构成二叉排序树的同时,还满足堆的性质(在这里我们假设节点的优先级大于该节点的孩子的优先级)。但是这里要注意的是Treap和二叉堆有一点不同,就是 二叉堆必须是完全二叉树,而Treap不一定是完全二叉树。 该博文主要讲解了Treap树相关的知识点及其实现。
Treap
我们都知道,在二叉查找树中,当插入的数据为随机的时候,其有较好的性能使得孩子节点大体上左右均匀分布。但是,当插入的数据为有序的时候,其会退化为一个链表的状态,从而达不到效果。一般,我们有AVL或者红黑树以及Splay等平衡二叉树结构。但是,其在实现上难度较高。为此,引入了Treap,treap采用了二叉堆的性质来保持二叉树的平衡性。因为对于一个堆而言,其需要满足如下的性质:一个节点的两个孩子节点的值都小于节点的本身的值。但是,对于一棵二叉查找树而言,其需要满足一棵树的左孩子节点的值小于根节点的值并且右孩子节点的值大于根节点的值。这显然出现了冲突。为此,我们需要增加一个变量,用于满足这样的性质。我们将用于满足二叉搜索树的性质的值称之为key,用于满足堆的性质的值称之为priority(优先级)。
每个节点的key我们是无法改变的,必须要按照要求来,但是为了保持treap的平衡性,我们只能从priority上做文章。其实也并没有复杂之处,就是让每个节点的priority都取一个随机值,这样我们就可以保证这棵树“基本平衡”。
treap的基本操作
为了要满足二叉堆和平衡树的性质,treap中有两种操作用于将不满足二叉堆的性质的二叉查找树进行相应的调整,使其满足相应的性质。这两个操作分别为左旋和右旋:
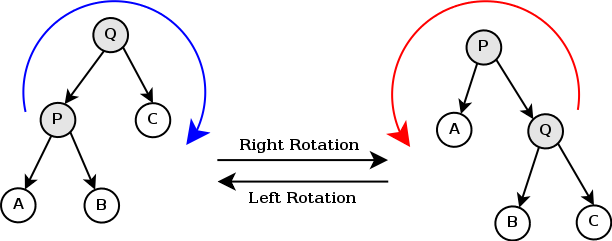
旋转操作的目的是使得不满足堆序的两个节点通过调整位置,使其重新满足堆序。且不改变二叉查找树的性质。
ps:我们知道,堆有两种形式,一种是大顶堆,一种是小顶堆,以下讨论的,我们采用小顶堆的方式对其进行操作
treap的相关操作
在对treap树进行相关的操作之前,我们先定义treap的节点类:
class Node{
/**
* 元素的关键字值
*/
T key;
/**
* 节点的优先级,用于满足堆的性质
*/
int priority;
/**
* 该节点的左右孩子节点
*/
Node left;
Node right;
/**
* 一个随机数生成器,用于随机生成节点的元素的优先级
*/
Random random=new Random();
public Node(T key){
this(key,null,null);
}
public Node(T key,Node left,Node right){
this.key=key;
this.left=left;
this.right=right;
this.priority=random();
}
treap相关的操作有插入、删除、查找。
查找:
treap的查找操作并不影响treap树相关的性质,其只需要按照普通的二叉查找树的检索方式进行查找即可。
具体代码如下:
/**
* 用于treap树的查找操作
* @param key 需要进行查找的关键字
* @return 查找的相应的节点,当没有找到对应的节点时,其返回null
*/
public Node search(T key){
Node temp=this.root;
while(temp!=null){
int cmp=key.compareTo(temp.key);
if(cmp<0){
temp=temp.left;
}
else if(cmp>0){
temp=temp.right;
}
else{
break;
}
}
return temp;
}
插入:
在Treap中插入元素,与在BST中插入方法相似。首先找到合适的插入位置,然后建立新的节点,存储元素。但是要注意建立新的节点的过程中,会随机地生成一个修正值,这个值可能会破坏堆序,因此我们要根据需要进行恰当的旋转。具体方法如下:
-
从根节点开始插入;
-
如果要插入的值小于等于当前节点的值,在当前节点的左子树中插入,插入后如果左子节点的修正值小于当前节点的修正值,对当前节点进行右旋;
-
如果要插入的值大于当前节点的值,在当前节点的右子树中插入,插入后如果右子节点的修正值小于当前节点的修正值,对当前节点进行左旋;
-
如果当前节点为空节点,在此建立新的节点,该节点的值为要插入的值,左右子树为空,插入成功。
其过程如下例:
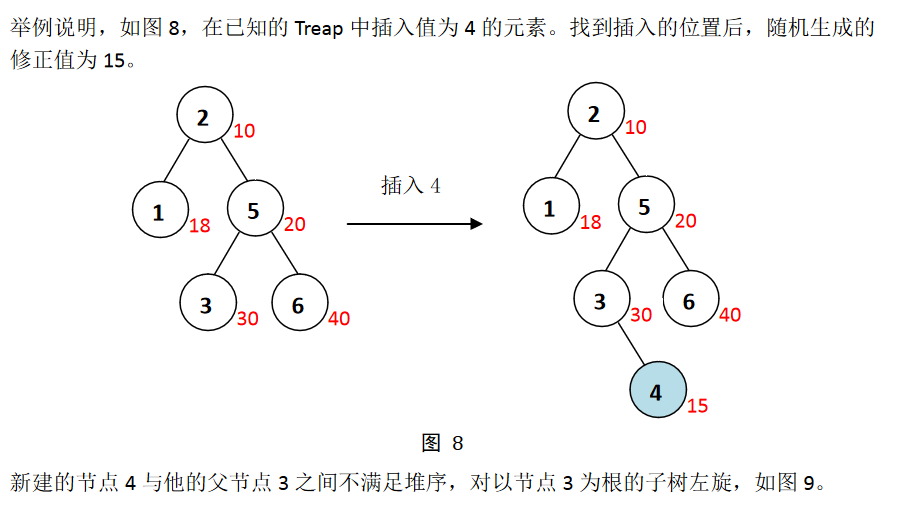
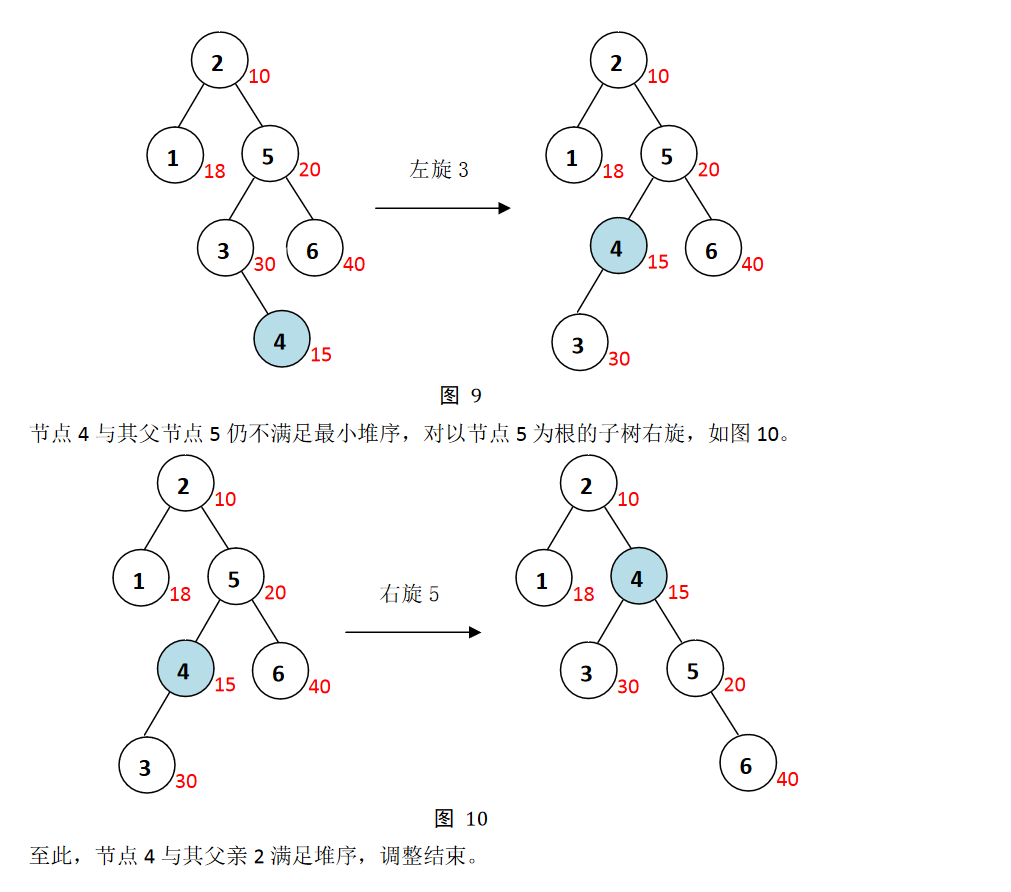
具体代码如下:
/**
* 用于往treap树中插入相应的节点
* @param key 节点元素的值
*/
public void insert(T key){
//当节点元素存在的时候
if(key==null||search(key)!=null){
return;
}
this.root=insert(this.root,key);
}
/**
* 用于插入元素相应的节点值
* @param node 需要进行比较的节点
* @param key 需要进行插入的键值
* @return 树对应的根节点
*/
private Node insert(Node node,T key){
if(node==null){
node=new Node(key);
}
else if(key.compareTo(node.key)<0){
node.left=insert(node.left,key);
//当满足情况的时候,对其进行旋转操作
if(node.left.priority<node.priority){
node=rotateRight(node);
}
}
else{
node.right=insert(node.right,key);
//当满足情况的时候,对其进行旋转操作
if(node.right.priority<node.priority){
node=rotateLeft(node);
}
}
return node;
}
删除:
与BST一样,在Treap中删除元素要考虑多种情况。我们可以按照在BST中删除元素同样的方法来删除Treap中的元素,即用它的后继(或前驱)节点的值代替它,然后删除它的后继(或前驱)节点并对其进行相应的旋转调整操作使其符合Treap中堆性质的要求。为了不使Treap向一边偏沉,我们需要随机地选取是用后继还是前驱代替它,并保证两种选择的概率均等。上述方法期望时间复杂度为O(logN),但是这种方法并没有充分利用Treap已有的随机性质,而是重新得随机选取代替节点。我们给出一种更为通用的删除方法,这种方法是基于旋转调整的。首先要在Treap树中找到待删除节点的位置,然后分情况讨论:
情况一, 该节点为叶节点或链节点(即只有一个孩子节点的节点),则该节点是可以直接删除的节点。若该节点有非空子节点,用非空子节点代替该节点的,否则用空节点代替该节点,然后删除该节点。
情况二, 该节点有两个非空子节点。我们的策略是通过旋转,使该节点变为可以直接删除的节点。如果该节点的左子节点的修正值小于右子节点的修正值,右旋该节点,使该节点降为右子树的根节点,然后访问右子树的根节点,继续讨论;反之,左旋该节点,使该节点降为左子树的根节点,然后访问左子树的根节点,继续讨论,直到变成可以直接删除的节点。(也就是让该节点的左右孩子节点中的最小优先级的节点称为该节点)
其过程如下例:
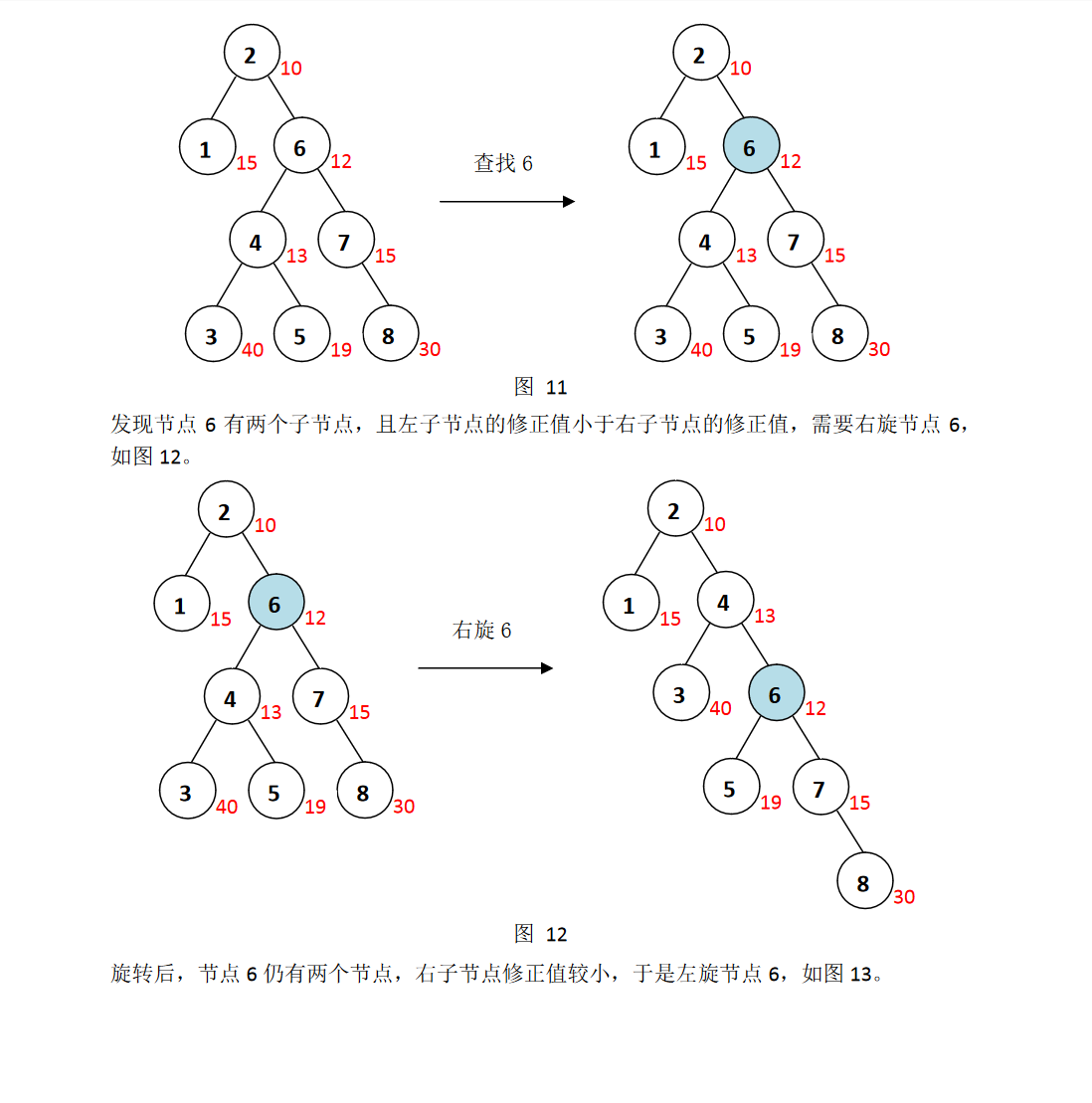
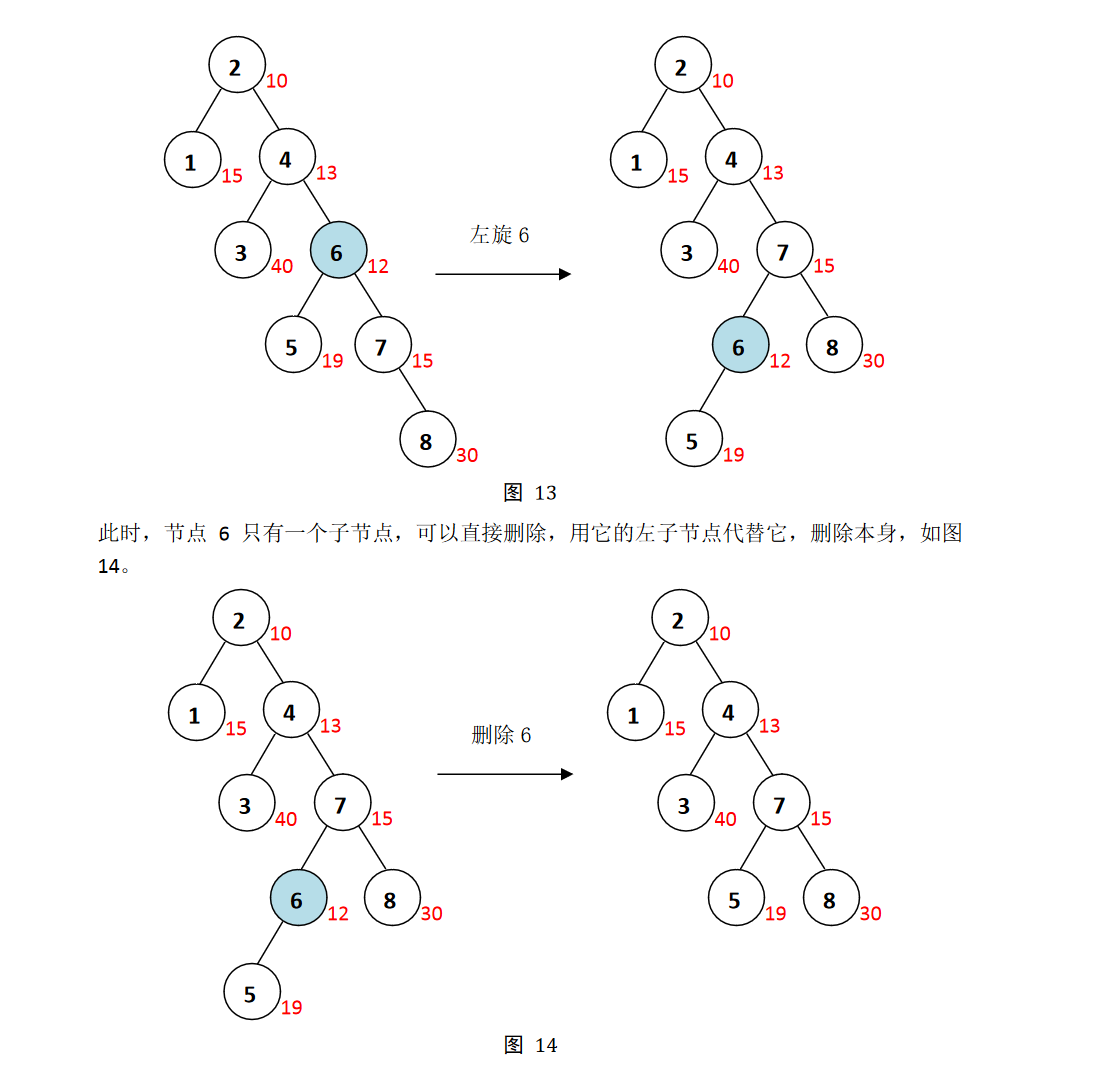
具体代码如下:
/**
* 节点的删除操作
* @param key 需要进行删除的节点的键值
*/
public void remove(T key){
//用于判空操作
if(key==null||search(key)==null){
return;
}
this.root=remove(this.root,key);
}
/**
* 删除对应的节点
* @param node 开始进行比较的节点
* @param key 进行删除的节点的关键字
* @return 其子树的根节点
*/
private Node remove(Node node,T key){
if(node==null){
return null;
}
//左子树
if (key.compareTo(node.key)<0){
node.left=remove(node.left,key);
}
//右子树
if(key.compareTo(node.key)>0){
node.right=remove(node.right,key);
}
//相等的情况,即删除的节点为该节点时
if(key.compareTo(node.key)==0){
//当存在左右孩子节点的时候
if(node.left!=null&&node.right!=null){
//如果左孩子优先级低就右旋
if(node.left.priority<node.right.priority){
node=rotateRight(node);
}
else{
node=rotateLeft(node);
}
//旋转后继续进行删除操作
node=remove(node,key);
}
else{
//当其为根节点的时候
if(node.left==null&&node.right==null){
return null;
}
//当其为单分支树的时候
node=node.left==null?node.right:node.left;
}
}
return node;
}
完整代码如下:
import java.util.Random;
/**
* @author 学徒
*用于实现Treap
*/
public class Treap<T extends Comparable<T>>{
/**
* 树的根节点
*/
private Node root;
/**
* 树的节点类
*/
private class Node{
/**
* 元素的关键字值
*/
T key;
/**
* 节点的优先级,用于满足堆的性质
*/
int priority;
/**
* 该节点的左右孩子节点
*/
Node left;
Node right;
/**
* 一个随机数生成器,用于随机生成节点的元素的优先级
*/
Random random=new Random();
public Node(T key){
this(key,null,null);
}
public Node(T key,Node left,Node right){
this.key=key;
this.left=left;
this.right=right;
this.priority=random();
}
/**
* 用于随机获取节点的优先级的随机数生成函数
* @return 随机数值
* 参考自:https://blog.csdn.net/chen_tr/article/details/50924073 随机数的生成。这样做,据说可以使得随机数的值
* 可以不发生重复
*/
private int random(){
int seed=random.nextInt();
return (int)(seed*48271L%Integer.MAX_VALUE);
}
}
/**
* 用于其相应的左旋操作
* @param node 进行旋转的节点
* @return 旋转后的根节点
*/
private Node rotateLeft(Node node){
Node temp=node.right;
node.right=temp.left;
temp.left=node;
return temp;
}
/**
* 用于其相应的右旋操作
* @param node 进行旋转的节点
* @return 旋转后的根节点
*/
private Node rotateRight(Node node){
Node temp=node.left;
node.left=temp.right;
temp.right=node;
return temp;
}
/**
* 用于treap树的查找操作
* @param key 需要进行查找的关键字
* @return 查找的相应的节点,当没有找到对应的节点时,其返回null
*/
public Node search(T key){
Node temp=this.root;
while(temp!=null){
int cmp=key.compareTo(temp.key);
if(cmp<0){
temp=temp.left;
}
else if(cmp>0){
temp=temp.right;
}
else{
break;
}
}
return temp;
}
/**
* 用于往treap树中插入相应的节点
* @param key 节点元素的值
*/
public void insert(T key){
//当节点元素存在的时候
if(key==null||search(key)!=null){
return;
}
this.root=insert(this.root,key);
}
/**
* 用于插入元素相应的节点值
* @param node 需要进行比较的节点
* @param key 需要进行插入的键值
* @return 树对应的根节点
*/
private Node insert(Node node,T key){
if(node==null){
node=new Node(key);
}
else if(key.compareTo(node.key)<0){
node.left=insert(node.left,key);
//当满足情况的时候,对其进行旋转操作
if(node.left.priority<node.priority){
node=rotateRight(node);
}
}
else{
node.right=insert(node.right,key);
//当满足情况的时候,对其进行旋转操作
if(node.right.priority<node.priority){
node=rotateLeft(node);
}
}
return node;
}
/**
* 节点的删除操作
* @param key 需要进行删除的节点的键值
*/
public void remove(T key){
//用于判空操作
if(key==null||search(key)==null){
return;
}
this.root=remove(this.root,key);
}
/**
* 删除对应的节点
* @param node 开始进行比较的节点
* @param key 进行删除的节点的关键字
* @return 其子树的根节点
*/
private Node remove(Node node,T key){
if(node==null){
return null;
}
//左子树
if (key.compareTo(node.key)<0){
node.left=remove(node.left,key);
}
//右子树
if(key.compareTo(node.key)>0){
node.right=remove(node.right,key);
}
//相等的情况,即删除的节点为该节点时
if(key.compareTo(node.key)==0){
//当存在左右孩子节点的时候
if(node.left!=null&&node.right!=null){
//如果左孩子优先级低就右旋
if(node.left.priority<node.right.priority){
node=rotateRight(node);
}
else{
node=rotateLeft(node);
}
//旋转后继续进行删除操作
node=remove(node,key);
}
else{
//当其为根节点的时候
if(node.left==null&&node.right==null){
return null;
}
//当其为单分支树的时候
node=node.left==null?node.right:node.left;
}
}
return node;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号