插入排序，希尔排序原理，代码及复杂度分析

插入排序算法

算法原理：
* 插入排序原理很简单，讲一组数据分成两组，
* 我分别将其称为有序组与待插入组。
* 每次从待插入组中取出一个元素，与有序组的元素进行比较，并找到合适的位置，
* 将该元素插到有序组当中。就这样，每次插入一个元素，有序组增加，待插入组减少。
* 直到待插入组元素个数为0。
* 当然，插入过程中涉及到了元素的移动。
*/

例如：45 80 48 40 22 78 
第一轮：45 80 48 40 22 78 ---> 45 80 48 40 22 78 i=1

第二轮：45 80 48 40 22 78 ---> 45 48 80 40 22 78 i=2

第三轮：45 48 80 40 22 78 ---> 40 45 48 80 22 78 i=3
第四轮：40 45 48 80 22 78 ---> 22 40 45 48 80 78 i=4
第五轮：22 40 45 48 80 78 ---> 22 40 45 48 78 80 i=5

图解：（图片来自网络  侵权删除）

实现代码如下：

 

public void InsertSort(int arr[]){
		int i,j,temp;
		for(i=1;i<arr.length;i++){//从第二个元素开始，第一个默认为有序的
			temp=arr[i];//准备排序的那个元素
			j=i-1;//排好序的数列的最后一个元素
			while(j>=0&&temp<arr[j]){//j>=0表示插入的边界，
				arr[j+1]=arr[j];//排序数列后移一个序列
				j--;
			}
			arr[j+1]=temp;
		}
		
	}

　时间复杂度：

最好情况（原本就是有序的）
比较次数：Cmin=n-1
移动次数：Mmin=0

最差情况（逆序）

比较次数：Cmax=2+3+4+……+n=(n+2)n/2
移动次数：Mmax=1+2+3+……+n-1=n*n/2

故时间复杂度为o(n^2)

 

希尔排序

算法原理：

先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量 =1(  <  …<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

图解（图片来自网络，侵权删除）

 

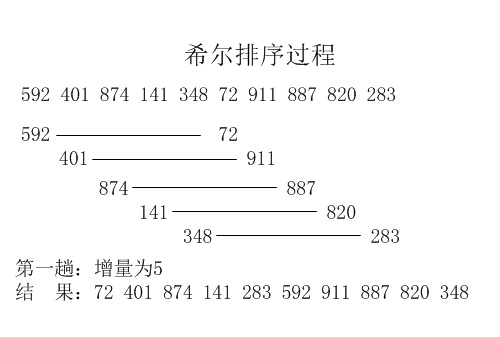
实现代码：

public  void  shellSort(int arr[]){
		int i,j,temp,len;
		len=arr.length;
		for(int step=len/2;step>0;step=step/2){//最外外层循环，根据步长分组
			//   for (step = len / 2; step > 0; step /= 2)  
			for(i=0;i<step;i++){//用直接插入法对每一组进行排序
				for(j=i+step;j<len;j=j+step){
					
					if(arr[j]<arr[j-step]){
						temp=arr[j];
						int k=j-step;//已经排序的最后一个元素的下标
						while(k>=0&&arr[k]>temp){
							arr[k+step]=arr[k];//排序序列右移步长个序列
							k=k-step;//找前一个元素
						}
						arr[k+step]=temp;//找到合适的位置 则直接插入
					}
				}
			}
		}
	}

　希尔排序的时间复杂度：

平均时间复杂度：希尔排序的时间复杂度和其增量序列有关系，这涉及到数学上尚未解决的难题；不过在某些序列中复杂度可以为O(n1.3);

 

排序方法	时间复杂度（平均）	时间复杂度（最坏)	时间复杂度（最好)	空间复杂度	稳定性	复杂性
直接插入排序	n2 O(n2)	O(n2)	O(n)	O(1)	稳定	简单
希尔排序	O(nlog2n)	n2 O(n2)	O(n)	O(1)	不稳定	较复杂

总结：

尔排序是基于插入排序的以下两点性质而提出改进方法的：

1. 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率。
2. 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位。