吴恩达机器学习第二课 Advanced Learning Algorithms
Advanced Learning Algorithms
week1
1.1 神经元和大脑

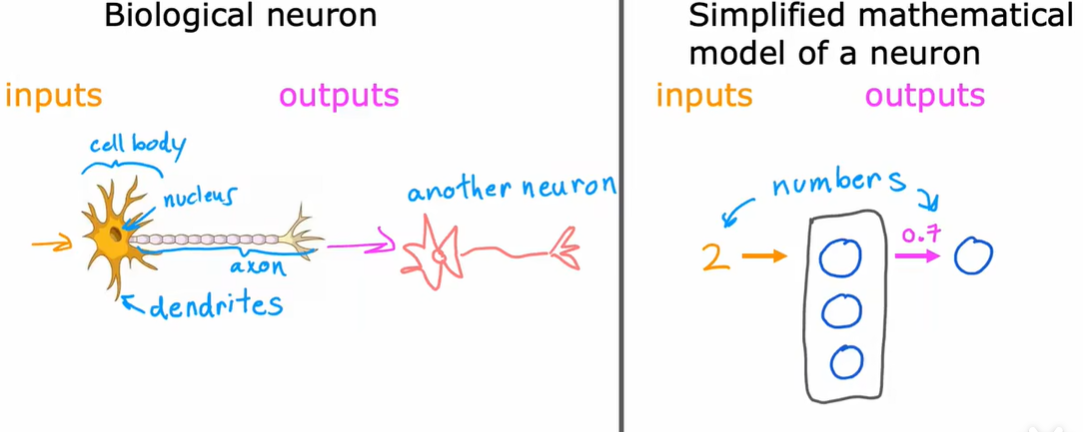
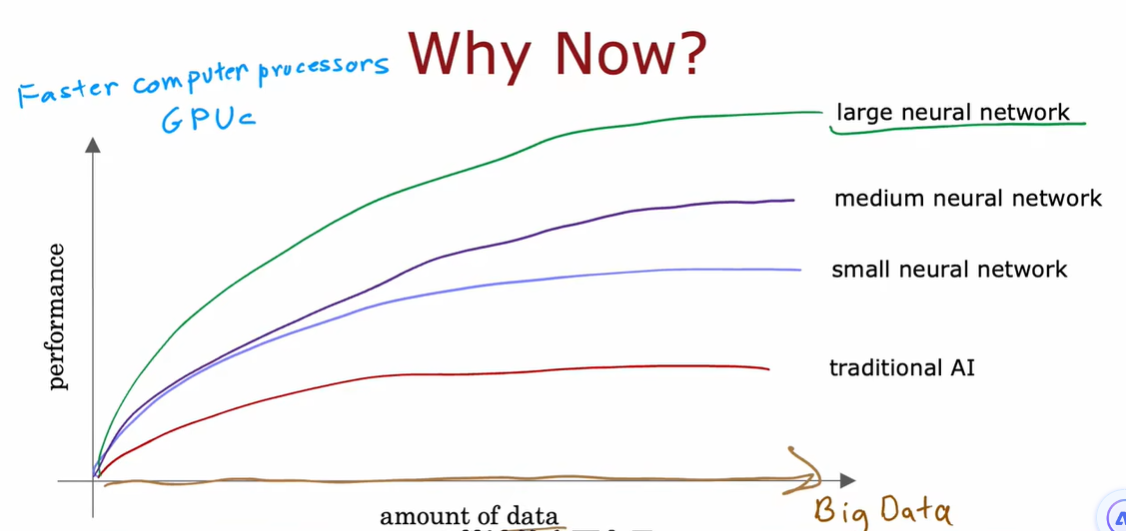
1.2 需求预测
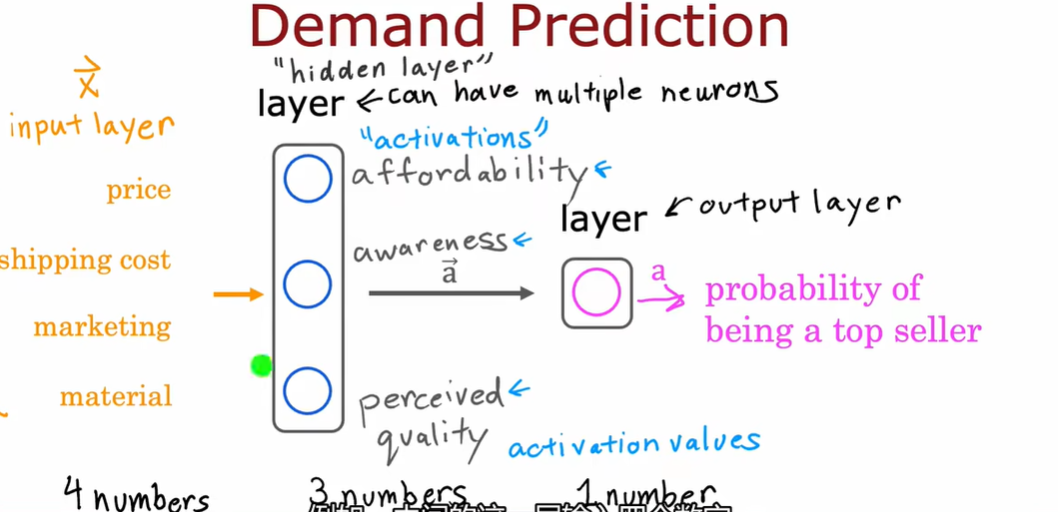
构建自己神经网络的时候:需要决定隐藏层的个数和每个隐藏层的神经元个数
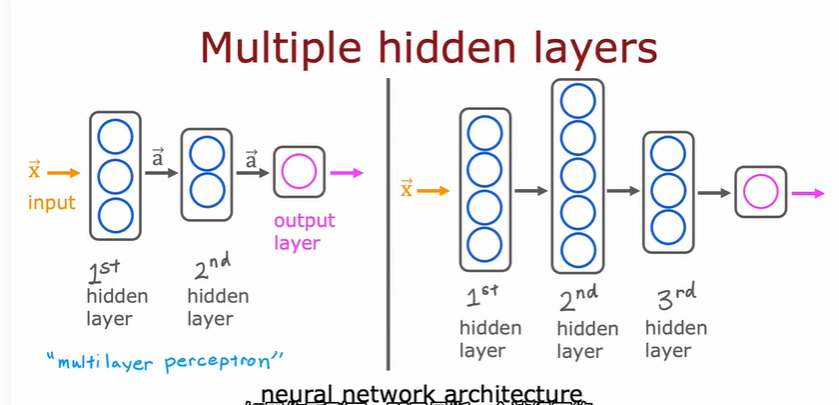
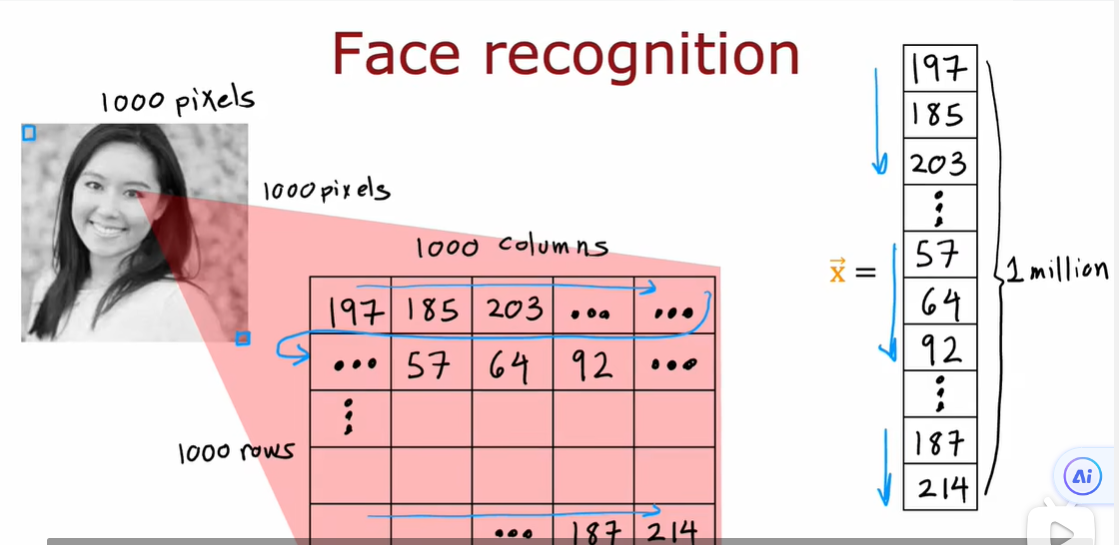
1.3 图像感知
像素的亮度值从0~255变化
人脸识别:训练一个神经网络,以一个特征向量作为输入,输出图片中人的身份
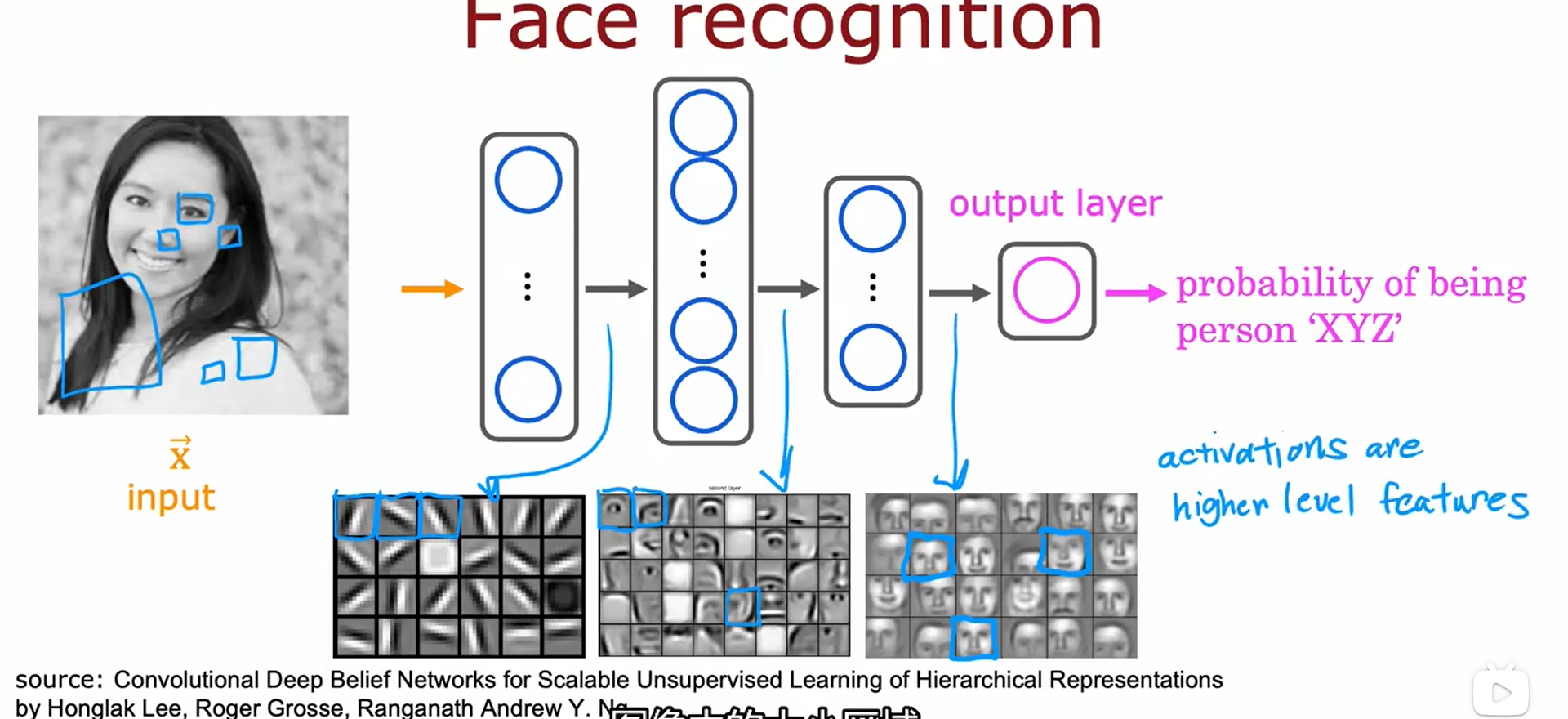
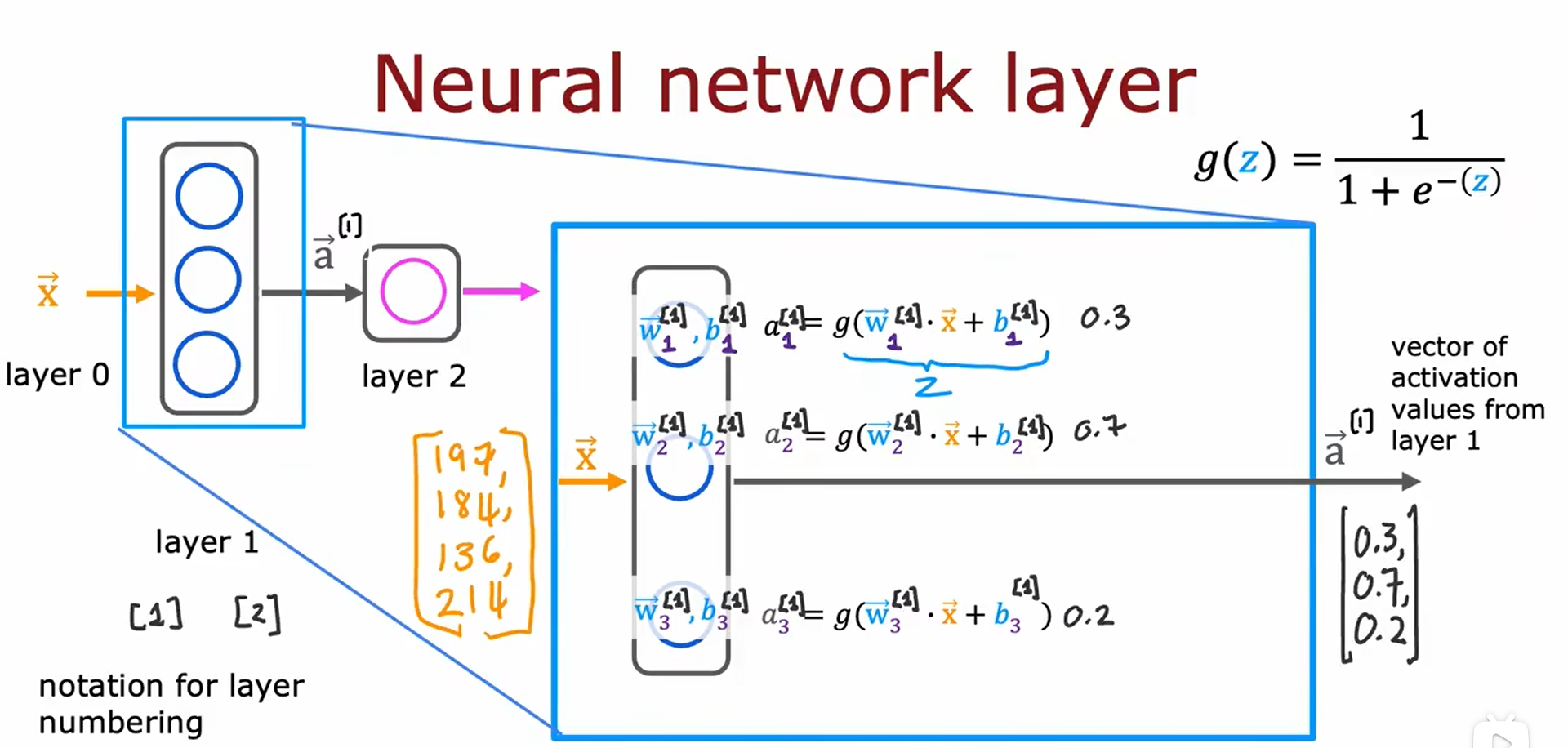
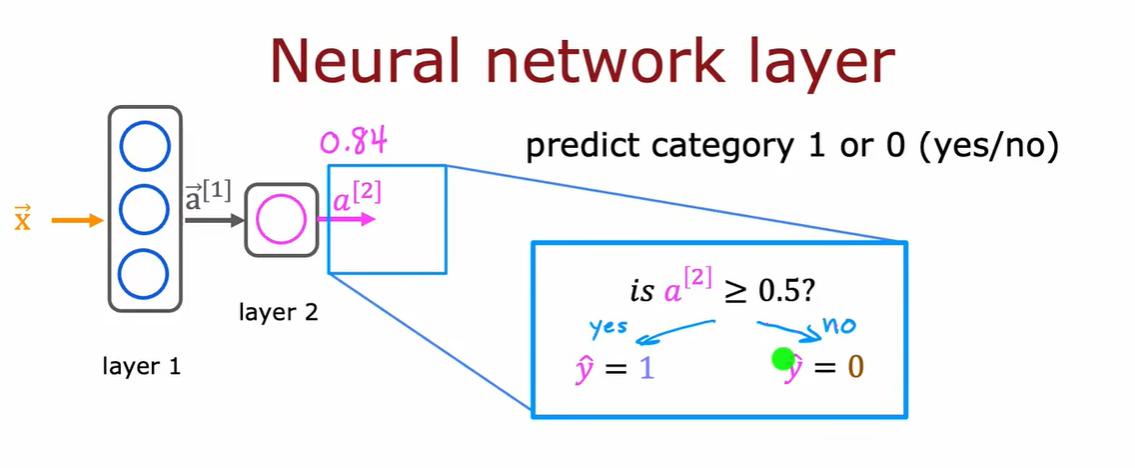
2.1 神经网络中的网络层
如何构建神经元层
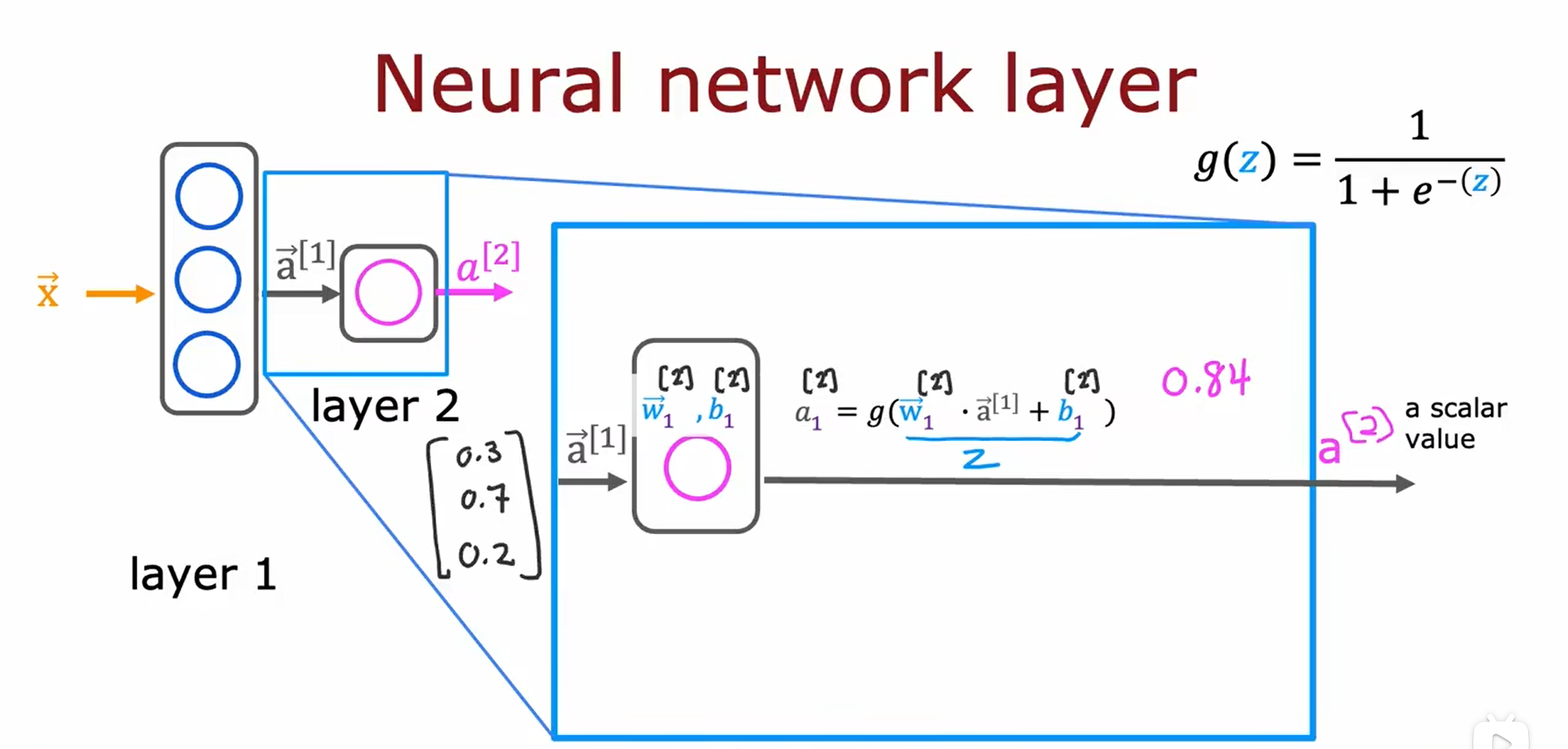
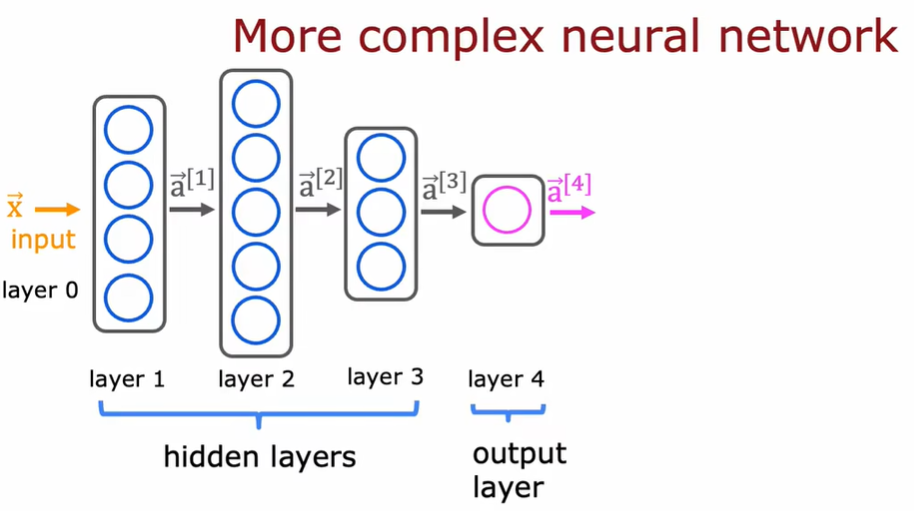
2.2 更复杂的神经网络
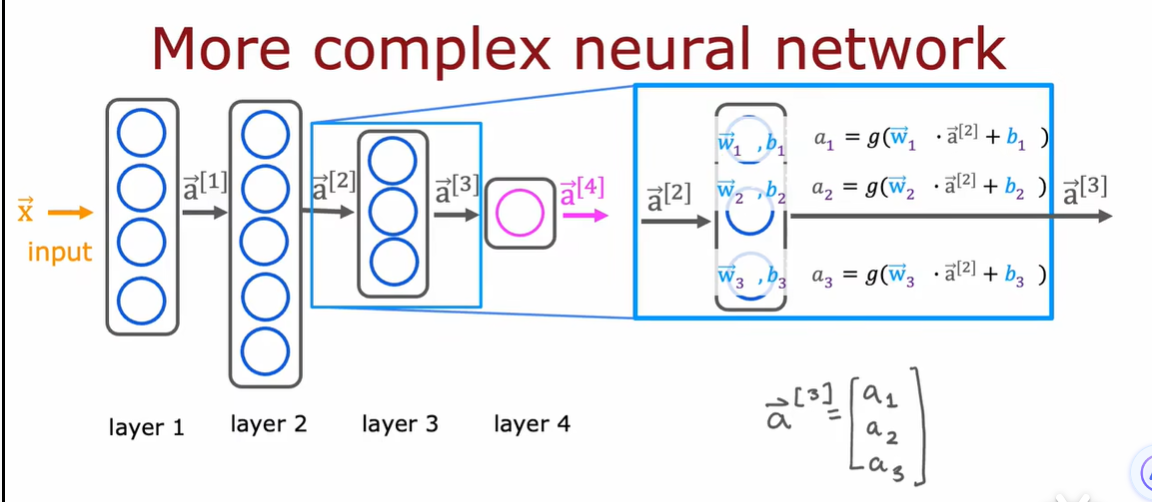

2.3 神经网络前向传播
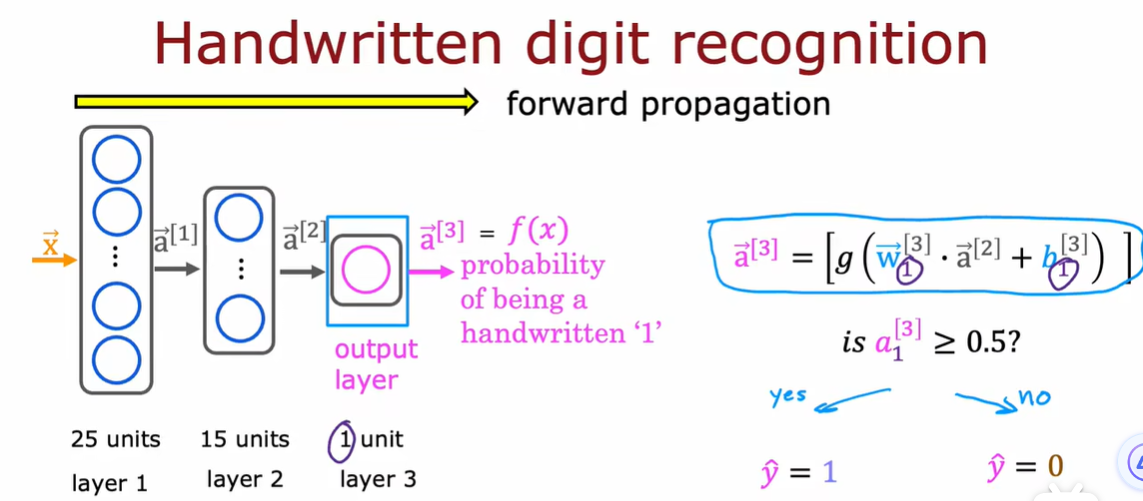
举例:手写数字识别
只区分手写数字0和1,二进制分类问题
8*8矩阵,255表示明亮的白色像素,0表示黑色像素
64个输入特征,使用两个隐藏层的神经网络
第一个隐藏层有25个神经元
第二个隐藏层有15个神经元
输出层是数字1的概率
第一次计算:\(\vec{x}\)(\(\vec{a}^{[0]}\))到\(\vec{a}^{[1]}\)
第二次计算:\(\vec{a}^{[1]}\)到\(\vec{a}^{[2]}\),这里\(\vec{a}^{[2]}\)是\(\vec{a}^{[1]}\)的一个函数
...
3.1 使用代码实现推理 tensorflow
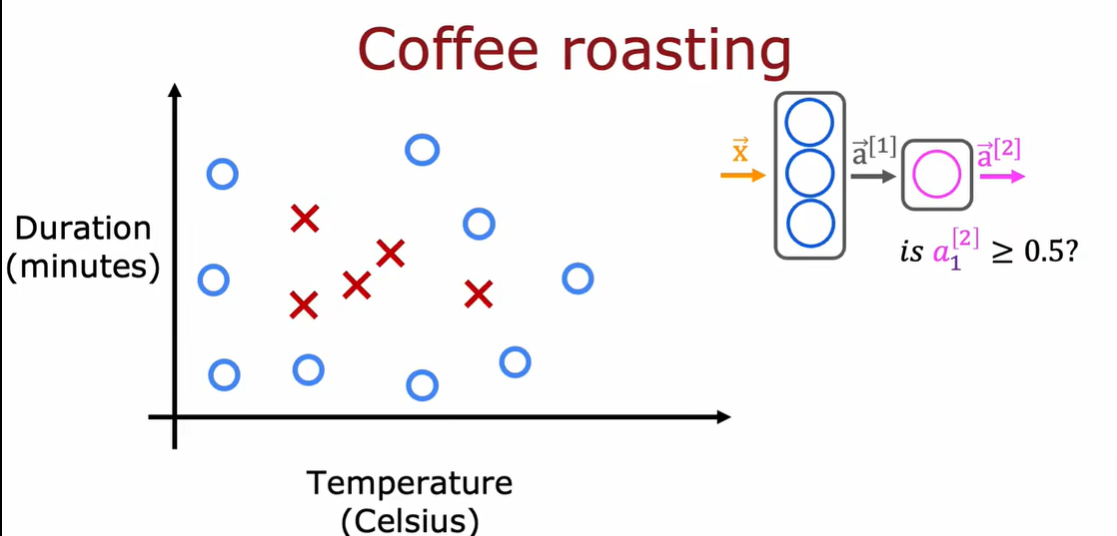
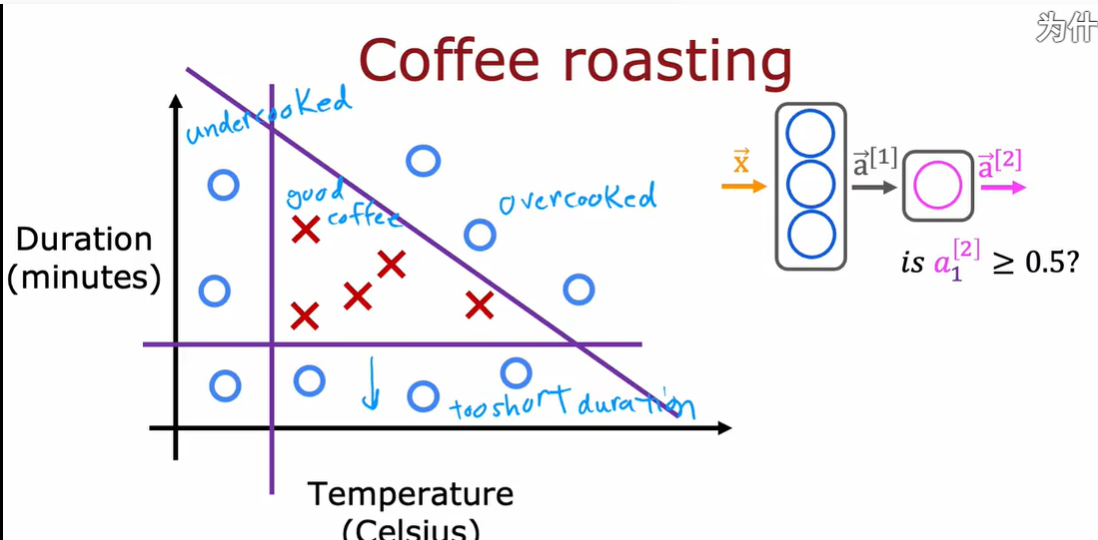
特征向量x:温度和持续时间
输出:是否是好咖啡
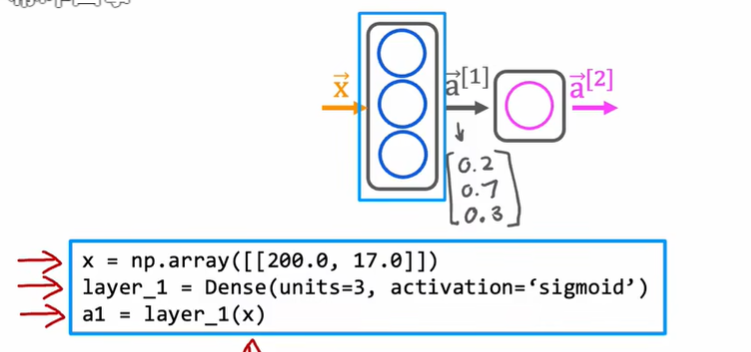

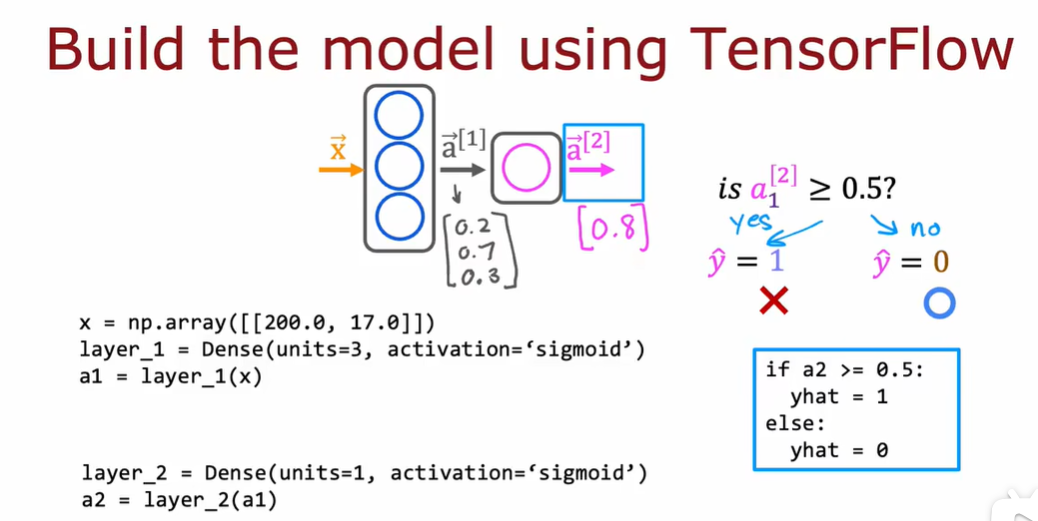
3.2 tensorflow的数据形式
在处理线性回归和逻辑回归的课程里,我们使用一维向量来表示输入特征x,对于tensorflow使用矩阵来表示数据
tensorflow处理数据集较大,使用矩阵可以让计算效率高一些

tensor是tensorflow团队为了更加有效的存储和执行矩阵计算创建的一种数据类型
从技术上来说,tensor比矩阵更通用,但是本课程会将tensor视为矩阵的一种表示方式
- 表示矩阵的tensorflow形式
- 表示矩阵的numpy形式

[!TIP]
如果想要获取张量a1并将其转换回numpy数组可以使用函数a1.numpy来实现
3.3 搭建一个神经网络

这里并没有对第一层和第二层的变量进行显式分配,通过sequential函数中。

下载tensorflow慢的话使用:
pip install --no-cache-dir tensorflow -i https://pypi.mirrors.ustc.edu.cn/simple/
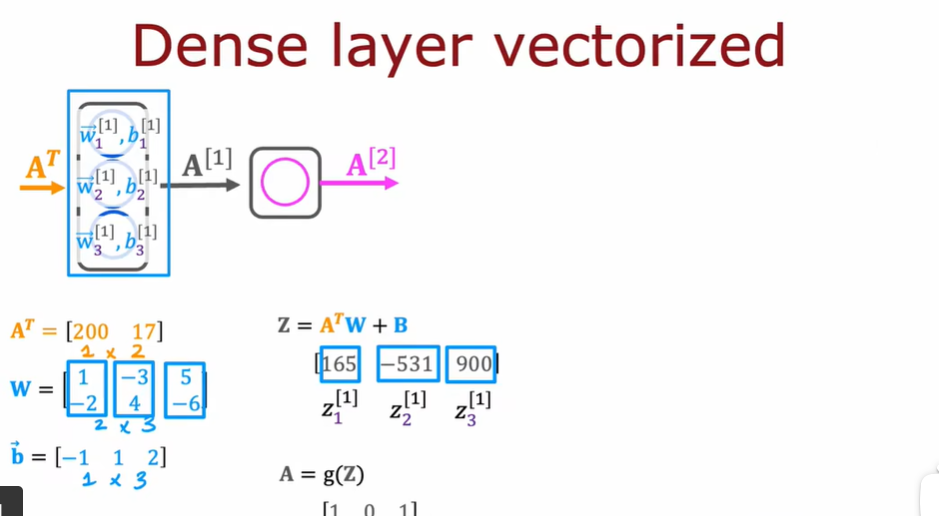
4.1 单个神经网络上的前向传播

4.2 前向传播的一般实现
编写一个函数来实现dense layer,即神经网络的单层
将前一层激活和给定层的神经元的参数w和b作为输入

W = np.array([
[1,-3,5],
[2,4,-6]
]) #w1是第一列,w2是第二列
b = np.array([-1,1,2])
a_in = np.array([-2,4])
def g(z):
return 1.0/(1.0+np.exp(-z))
def dense(a_in, W, b, g):
# 将前一个层的activation和给定神经元中的参数w和b作为输入
#给出本层的activation
units = W.shape[1] #有多少列 w.shape:(2,3) 有多少列就是有多少个单元
a_out = np.zeros(units) # [0,0,0]
for j in range(units):
w = W[:j] #依次把每一列取出来 0 :[1 2] 1 :[-3 4] 2 :[ 5 -6]
z = np.dot(w,a_in)+b[j]
a_out[j] = g(z)
return a_out
def sequential(x):
a1 = dense(x,W1,b1)
a2 = dense(a1,W2,b2)
a3 = dense(a2,W3,b3)
a4 = dense(a2,W4,b4)
f_x = a4
return f_x
5.1 强人工智能

6.1 神经网络
np.dot:这个函数既可以用于计算两个数组的点积(内积),也可以用于执行矩阵乘法。
np.matmul:此函数主要用于矩阵乘法。它要求参与计算的数组满足矩阵乘法的规则,即第一个数组的列数必须等于第二个数组的行数
def dense2(a_in, W, b):
z = np.matmul(a_in,W)+b #主要用于矩阵乘法
a_out = g(z)
return a_out
6.2 矩阵乘法及其实现
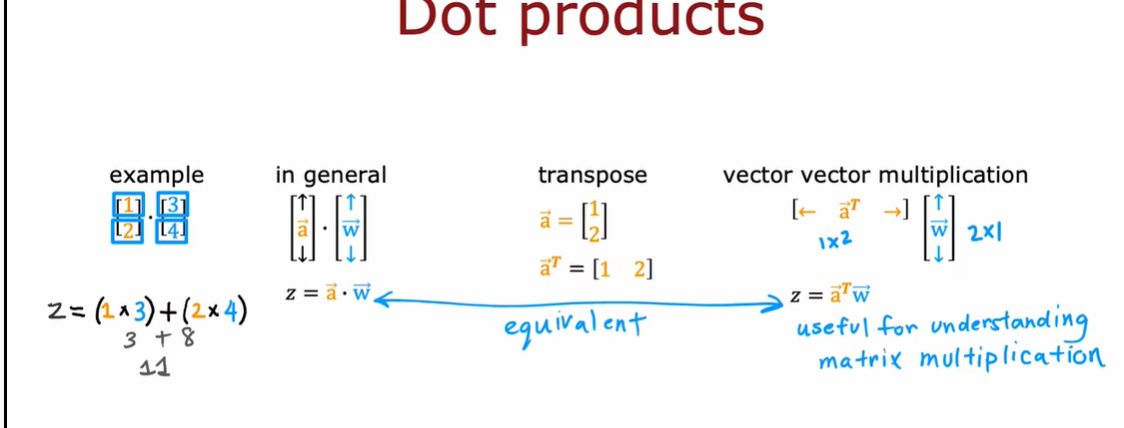
使用 vectorization
a = np.array([1,2]) #生成数组 (2,)
b = np.array([3,4])
z = np.dot(a,b) # 1*3+2*4
z # 11
a = np.array([1,2]).reshape(1,-1)
b = np.array([3,4])
z = np.dot(a,b)
z # array([11])

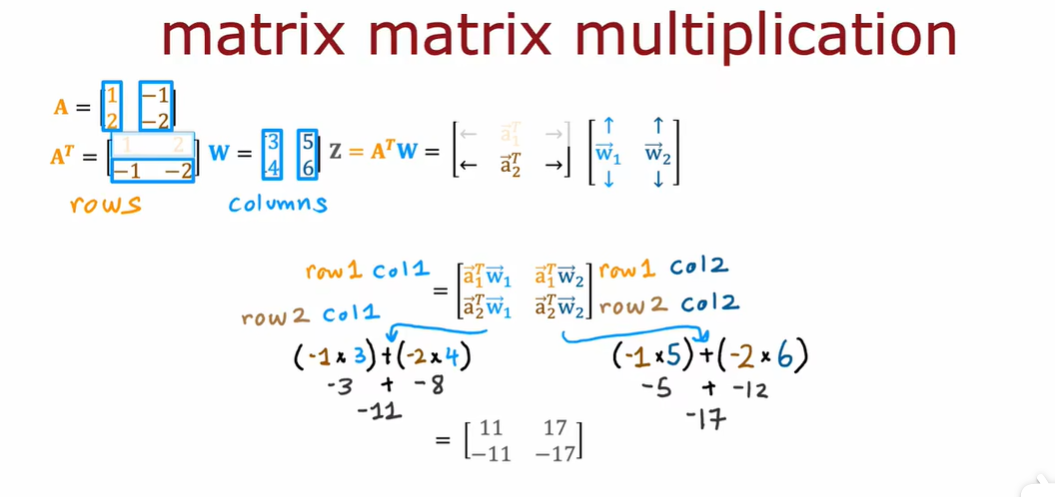

A = np.array([[1,-1,0.1],[2,-2,0.2]])
AT = A.T
W = np.array([[3,5,7,9],[4,6,8,0]])
Z = np.matmul(AT,W)
#Z = AT @ W
Z
week2
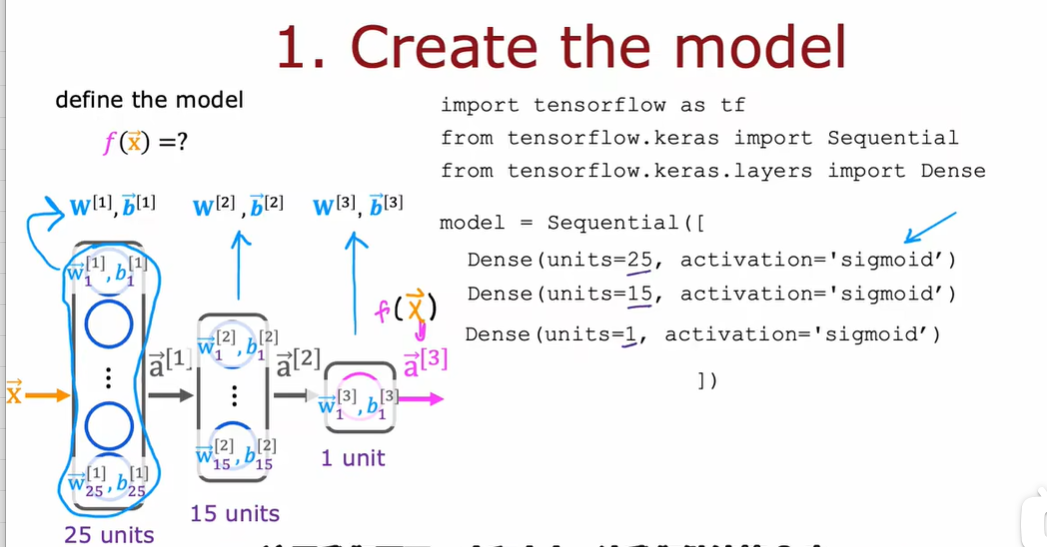
1.1 Tensorflow实现
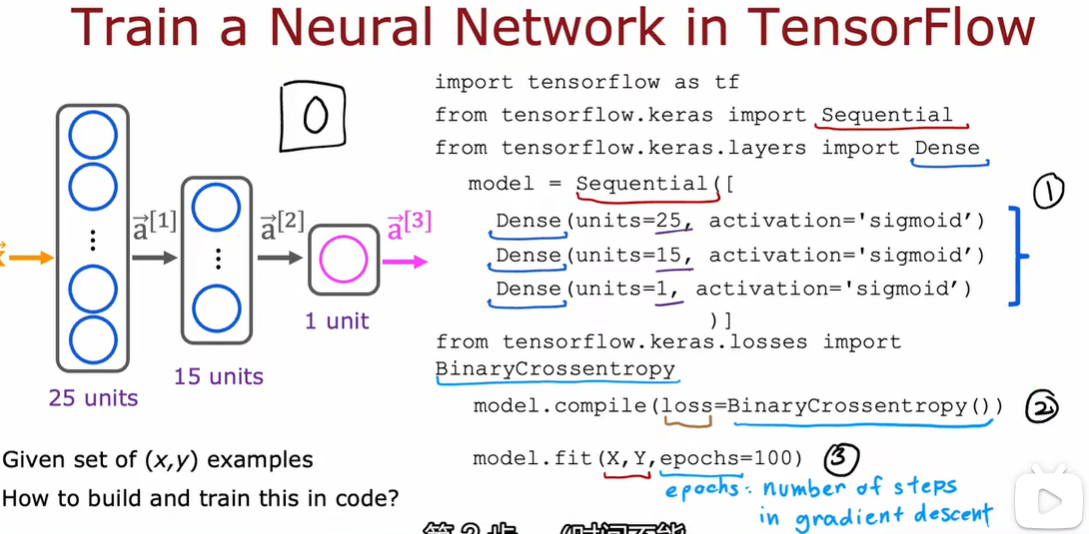
1.2 模型训练细节



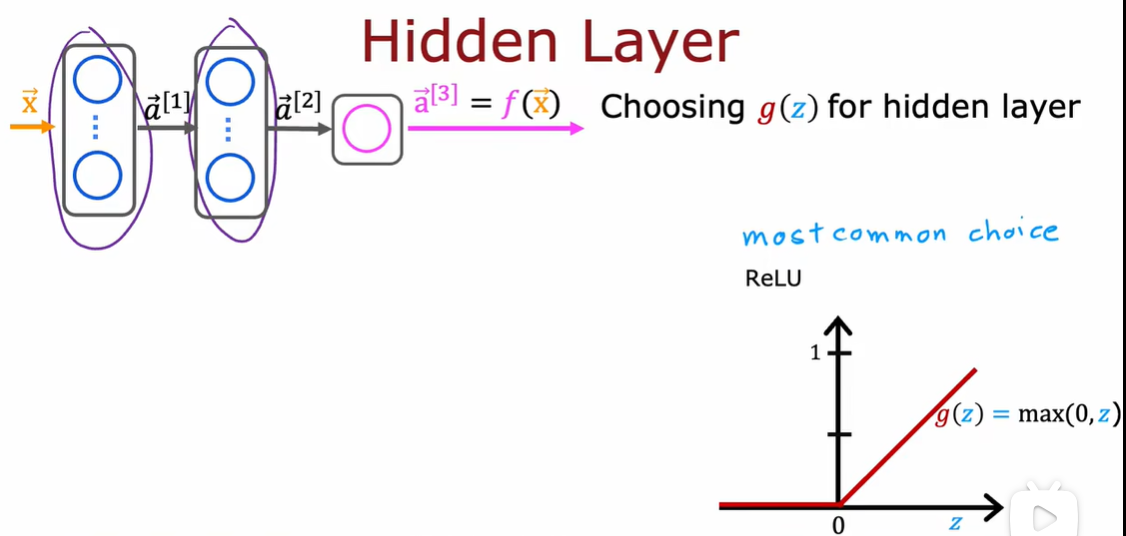
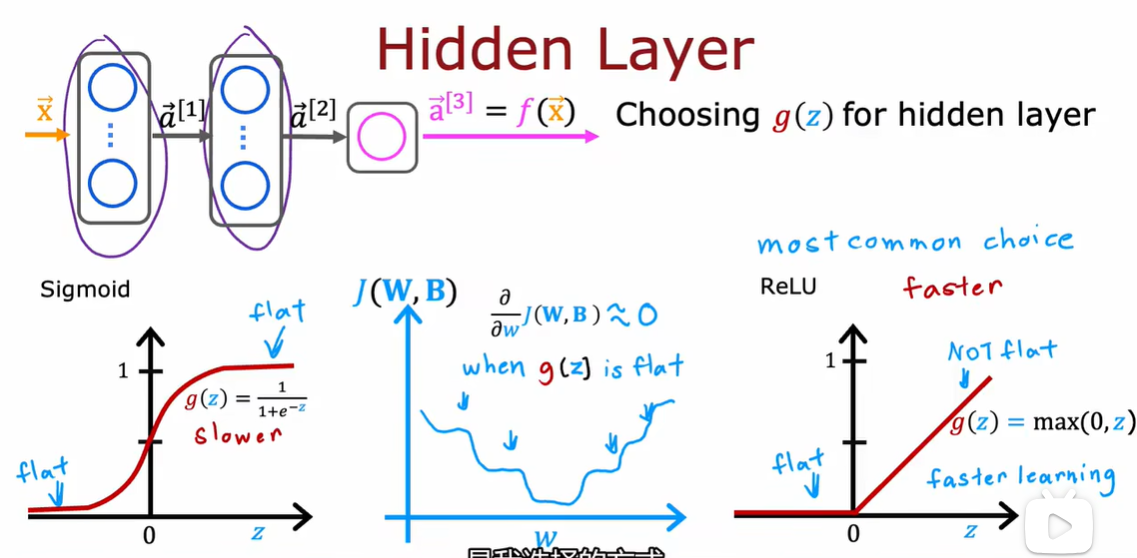
2.1 Sigmoid 激活函数的替代方式
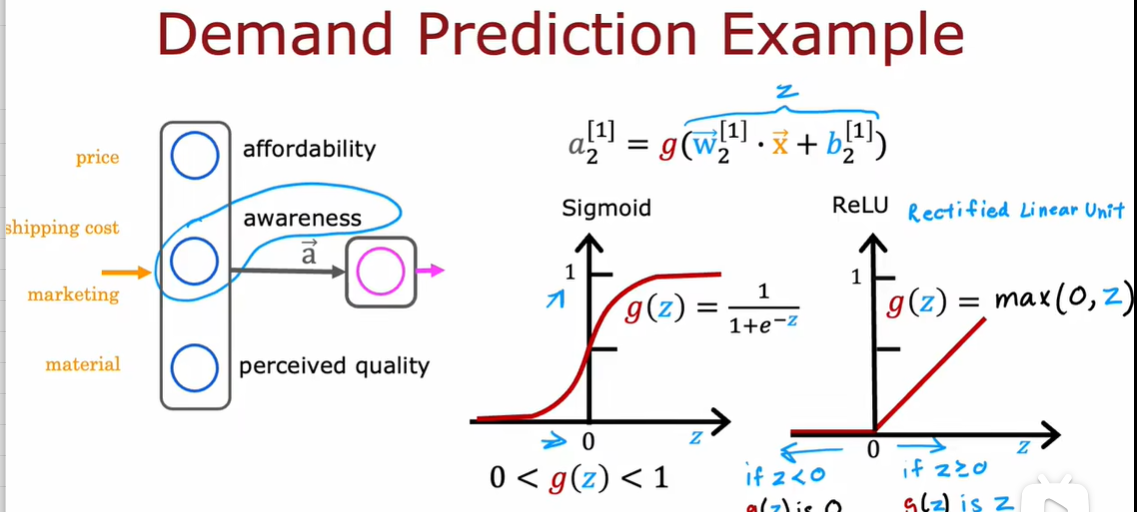
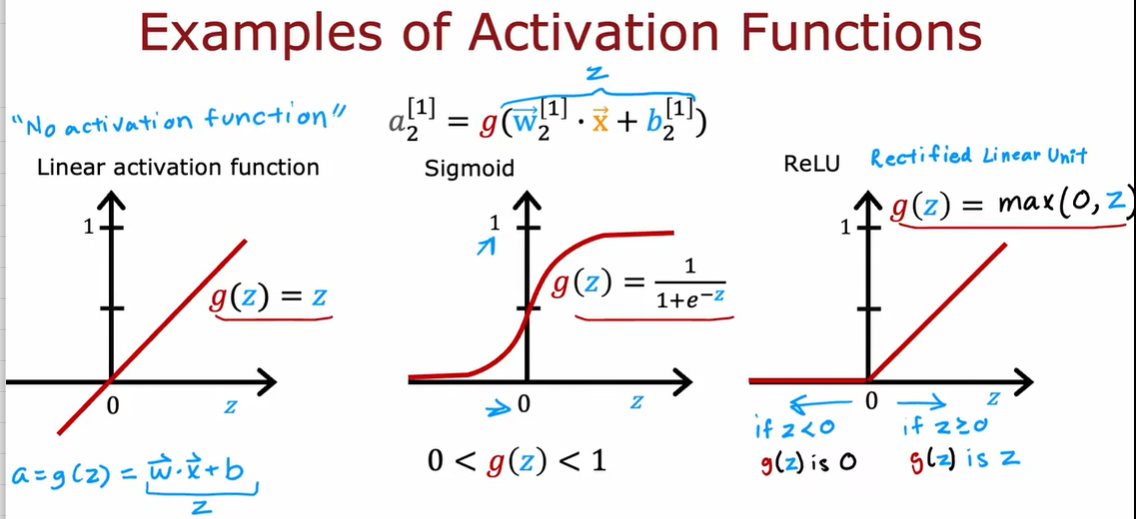
2.2 如何选择激活函数
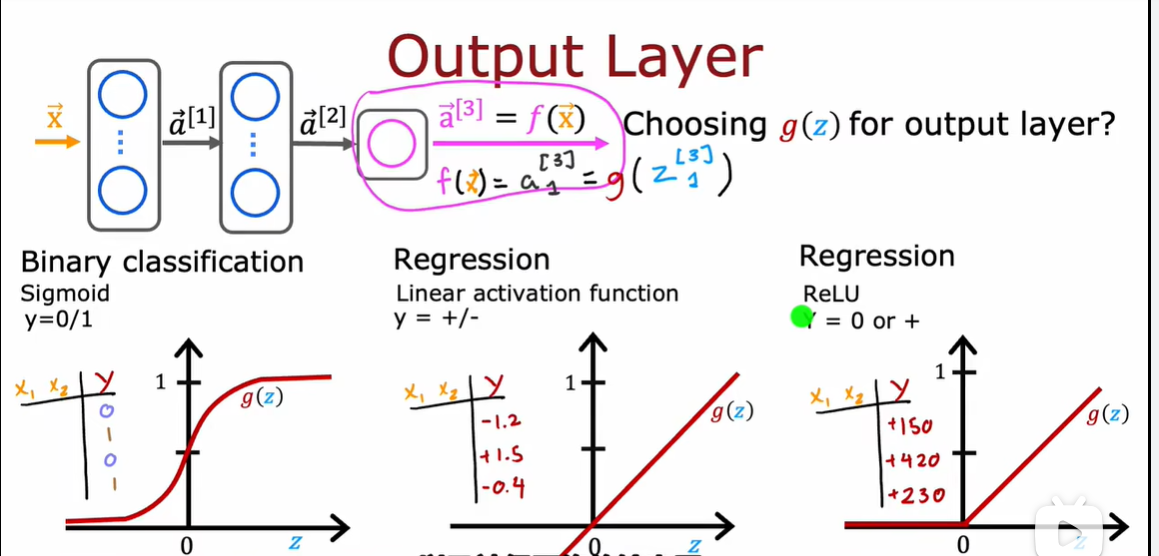

2.3 为什么模型需要激活函数
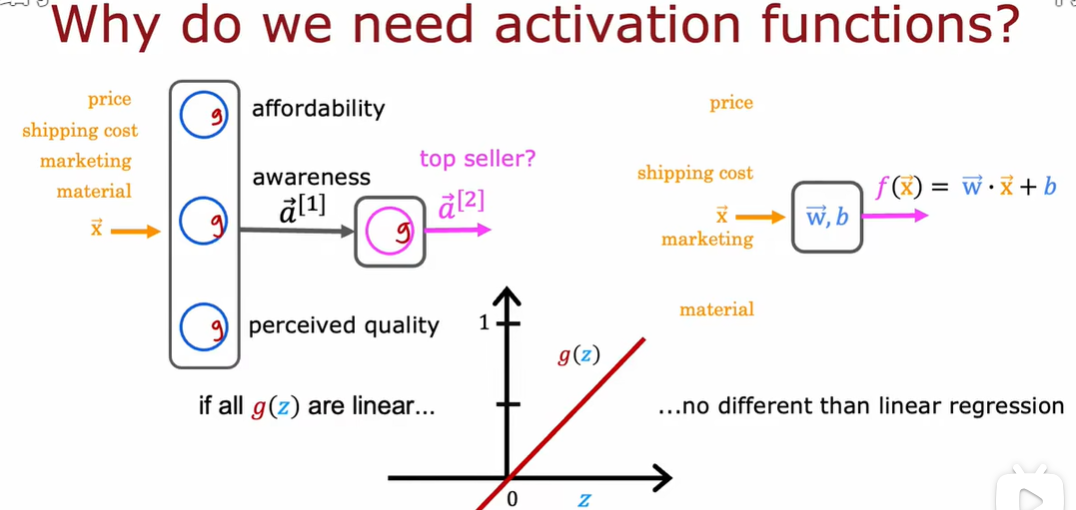
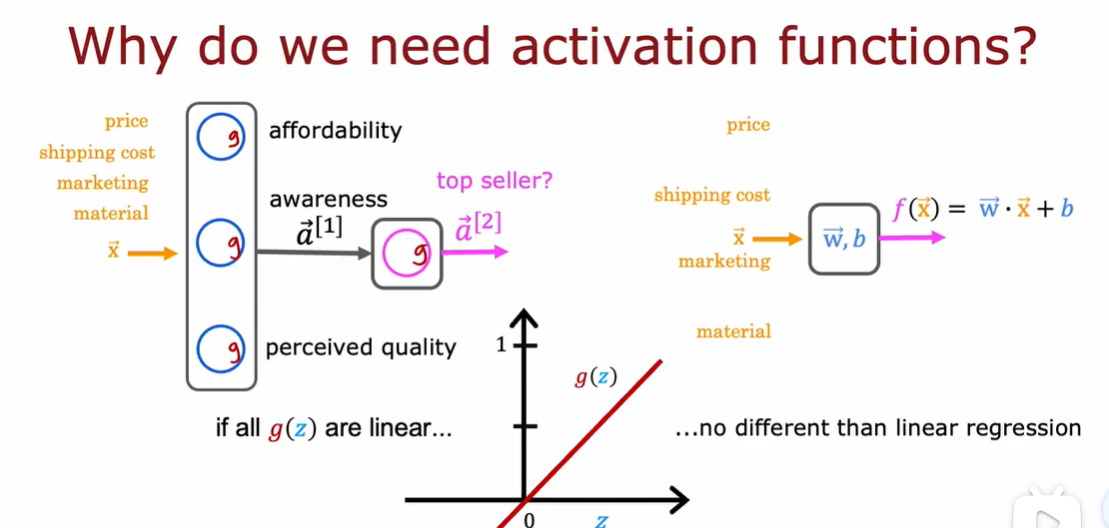
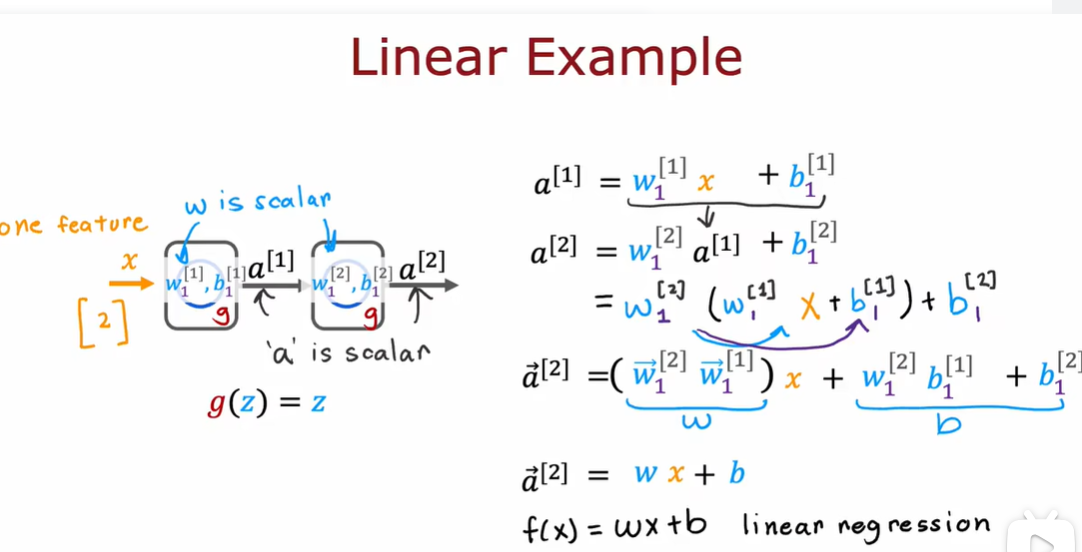
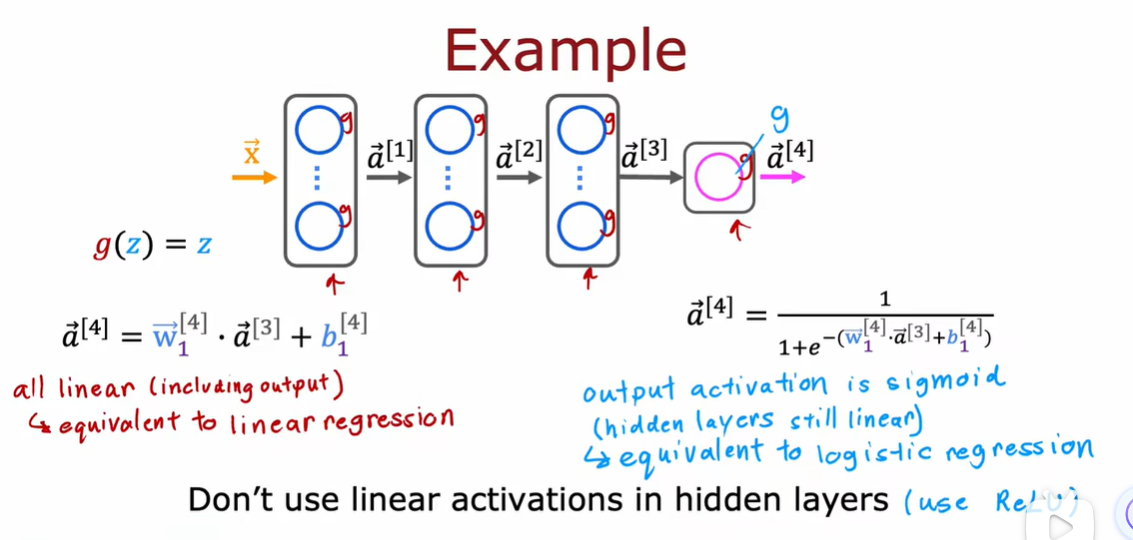
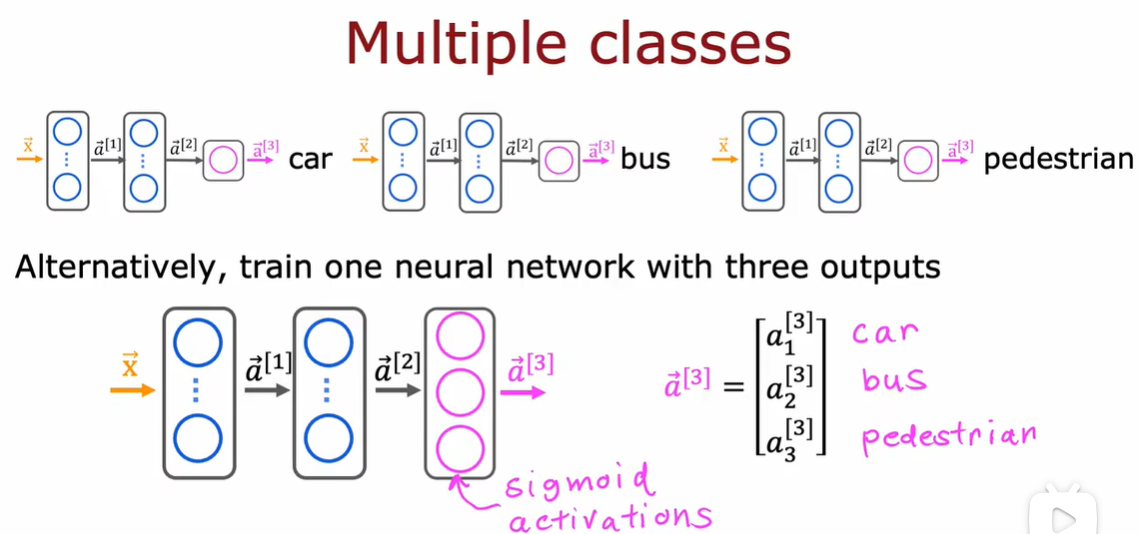
3.1 多分类问题
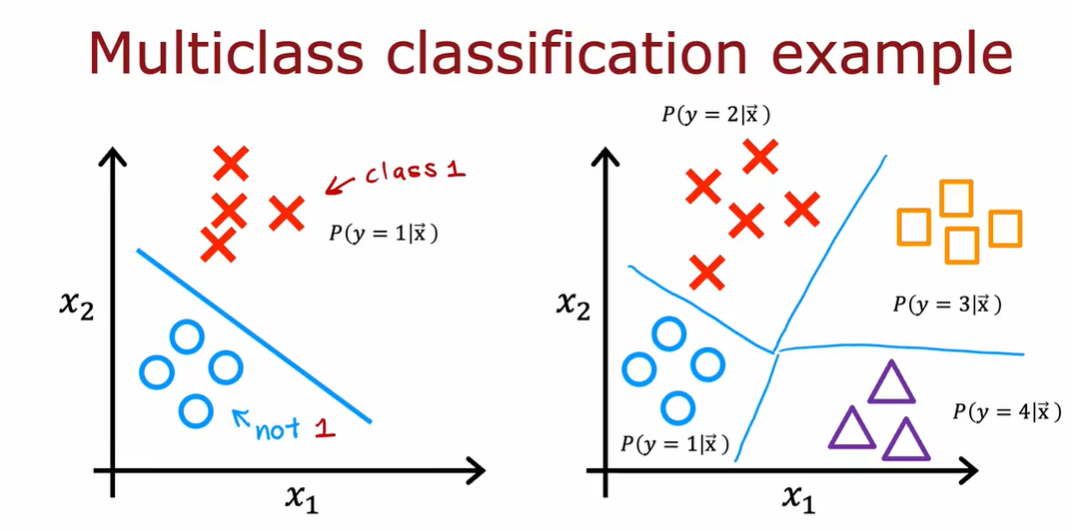
3.2 softmax

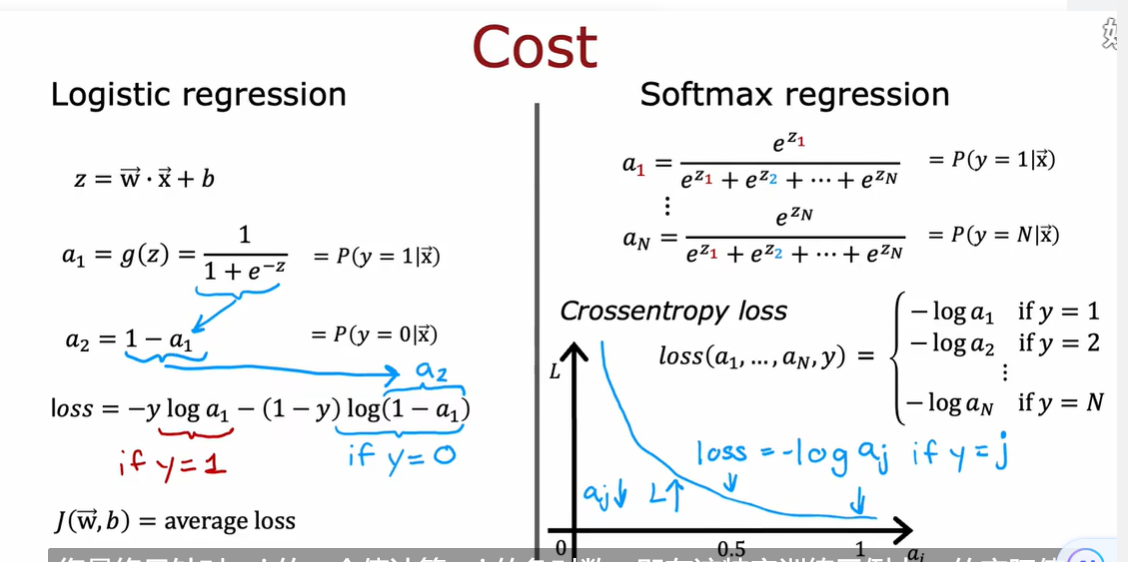
3.3 神经网络的Softmax输出
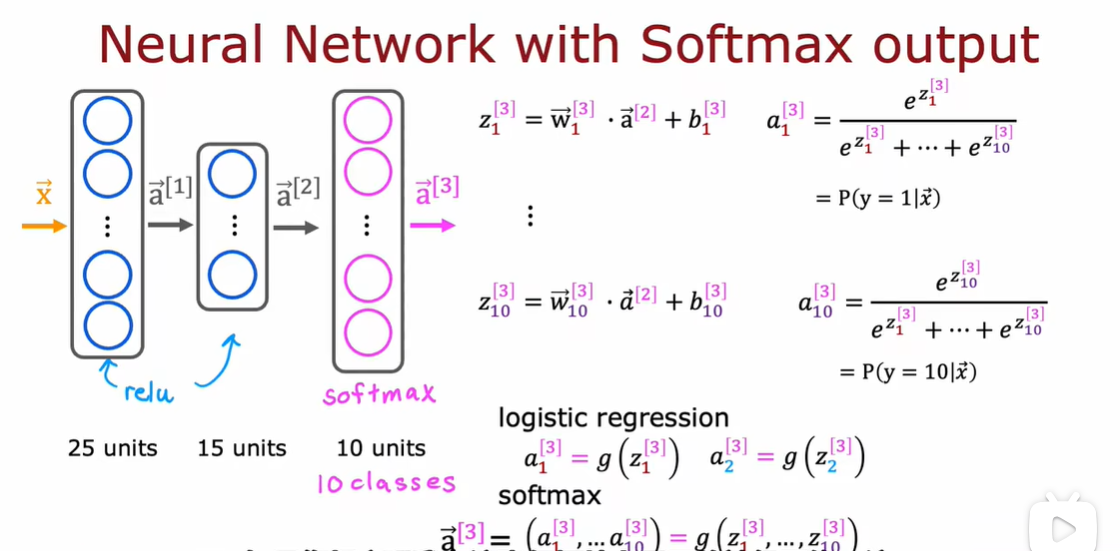

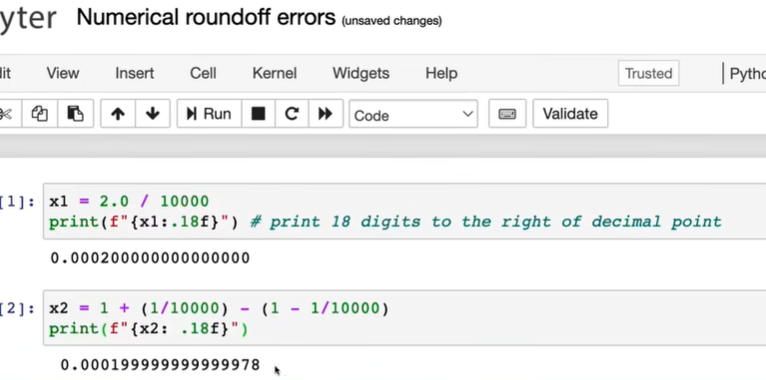
3.4 Softmax的改进实现



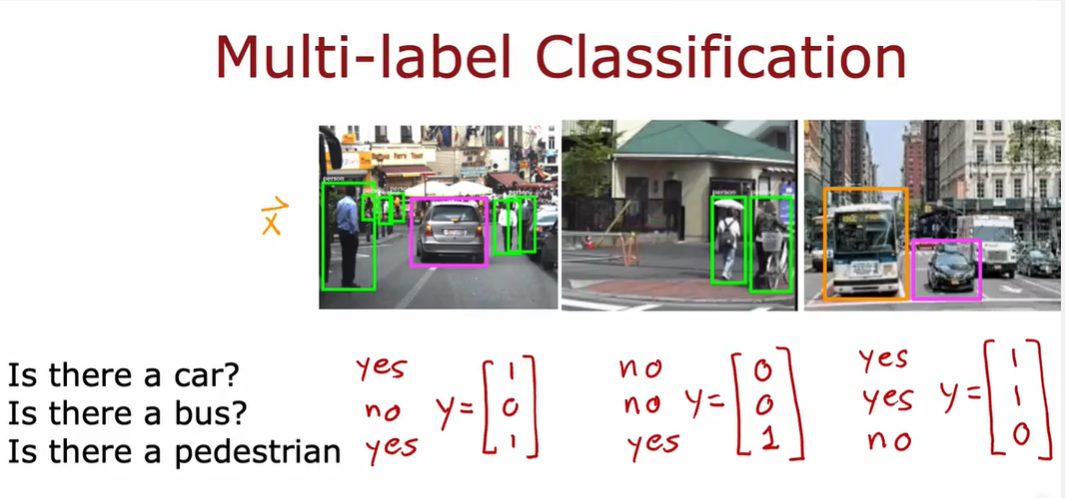
3.5 多个输出的分类
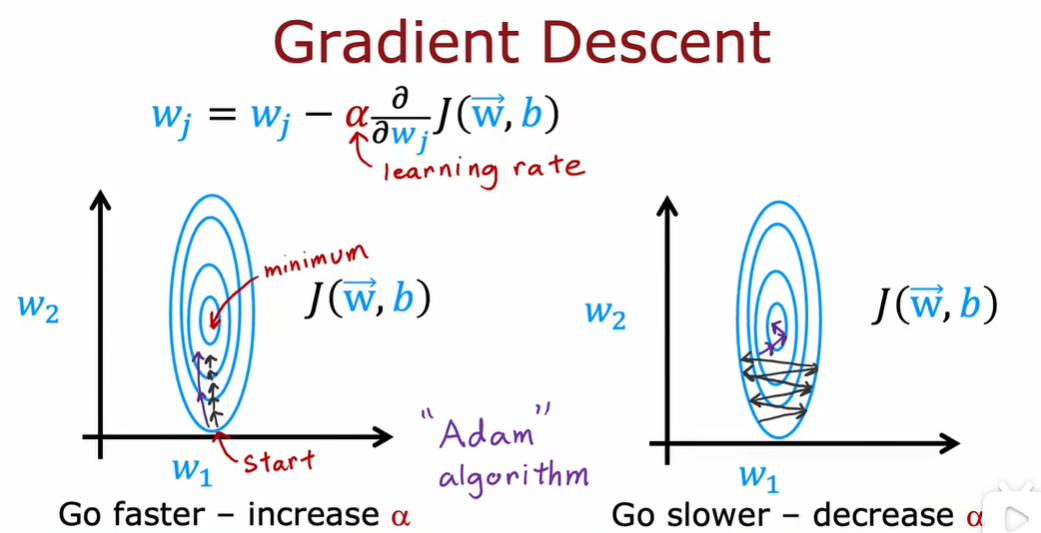
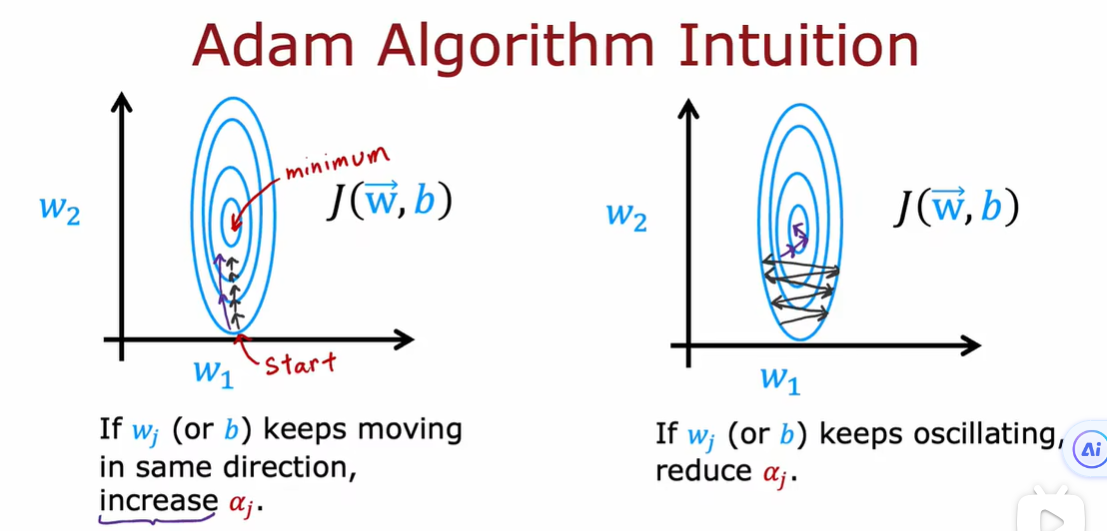
4.1 高级优化方法


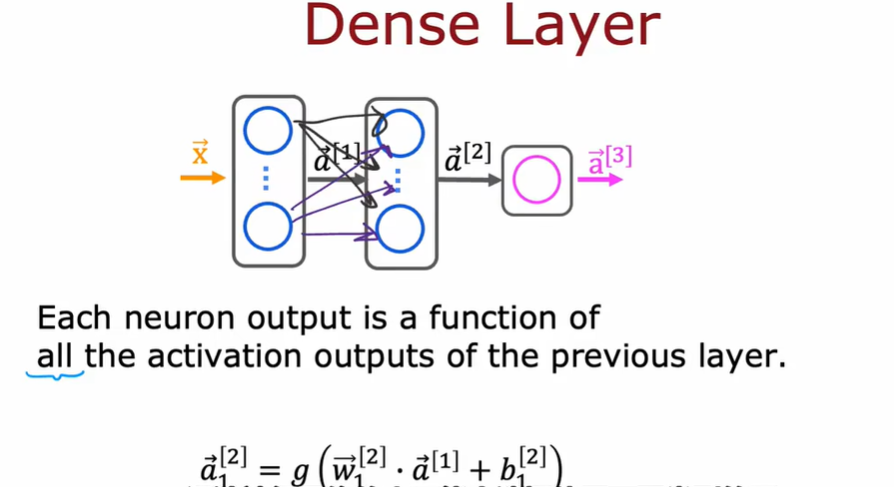
4.2 其他的网络层类型
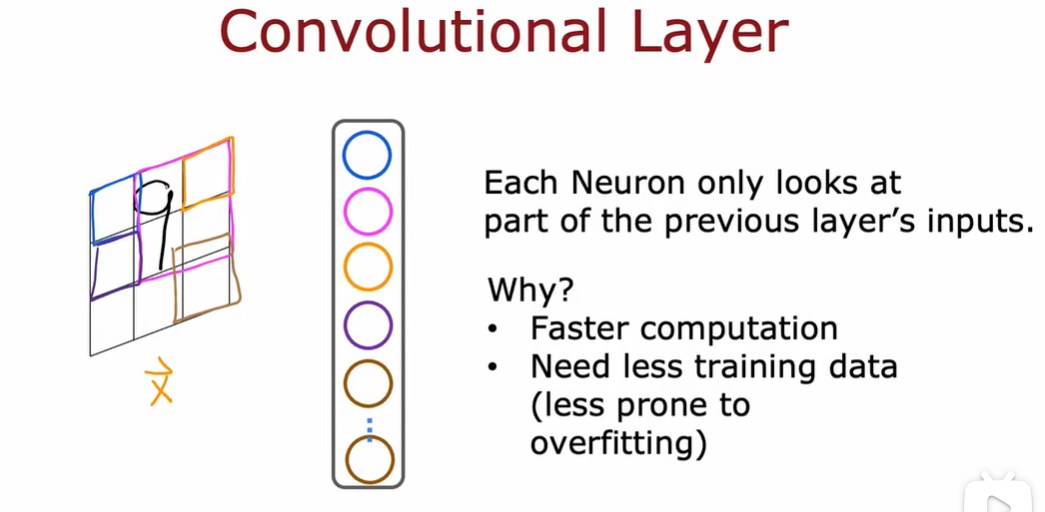
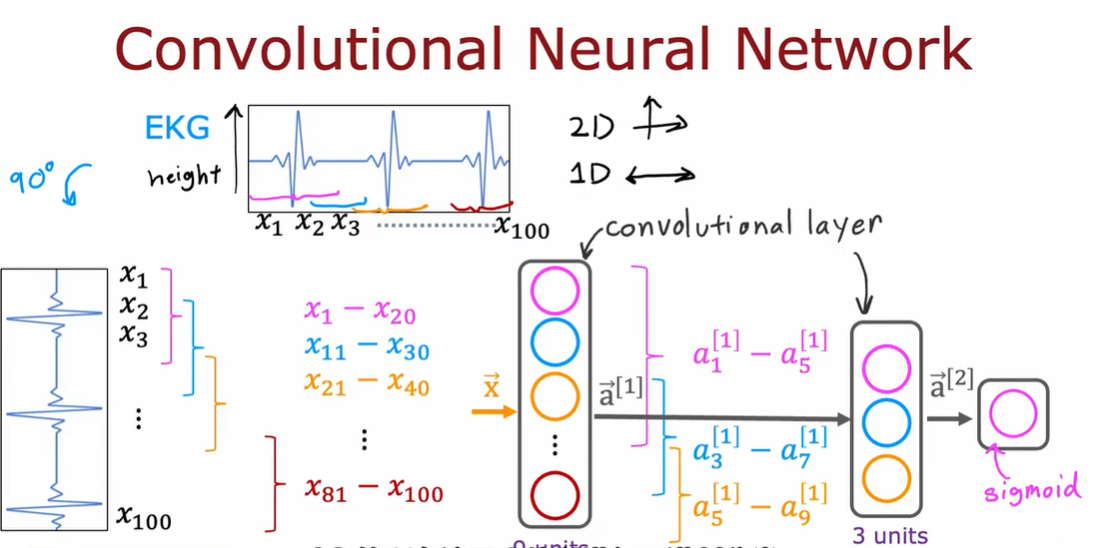
5.1 什么是导数(选修)



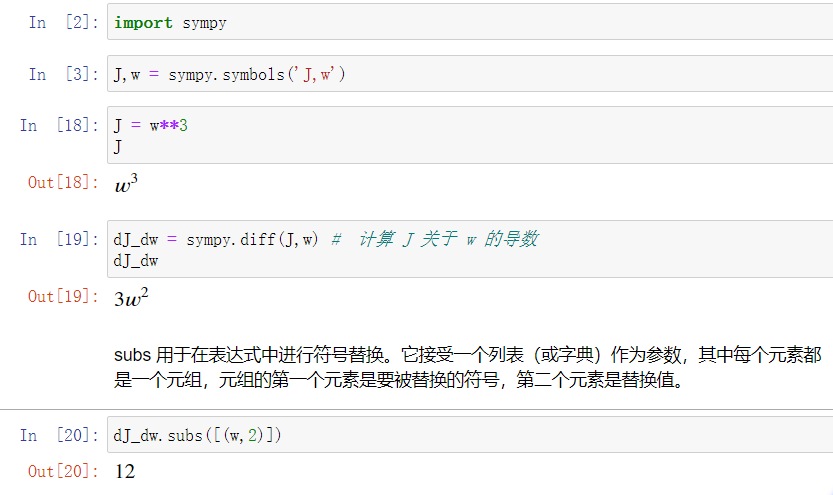
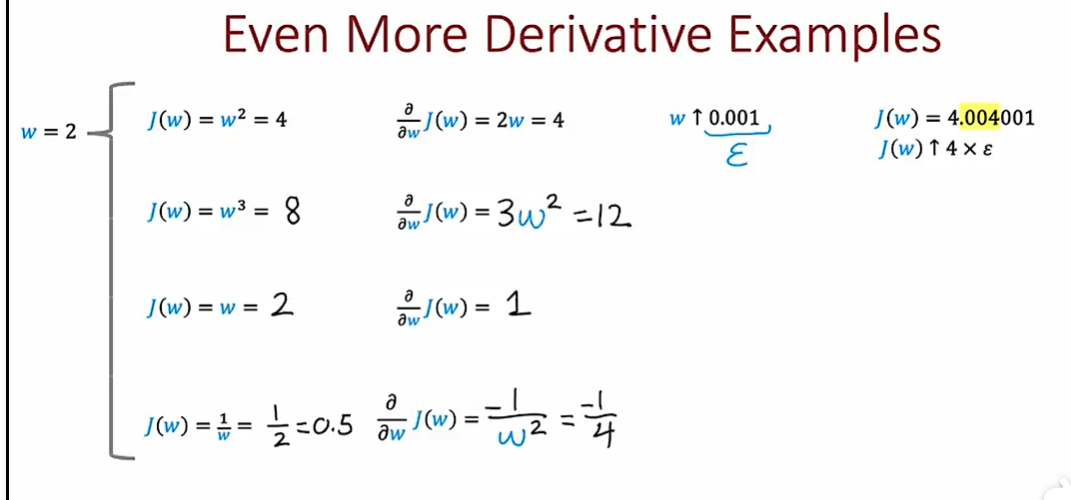


5.2 计算图




5.3 大型神经网络案例
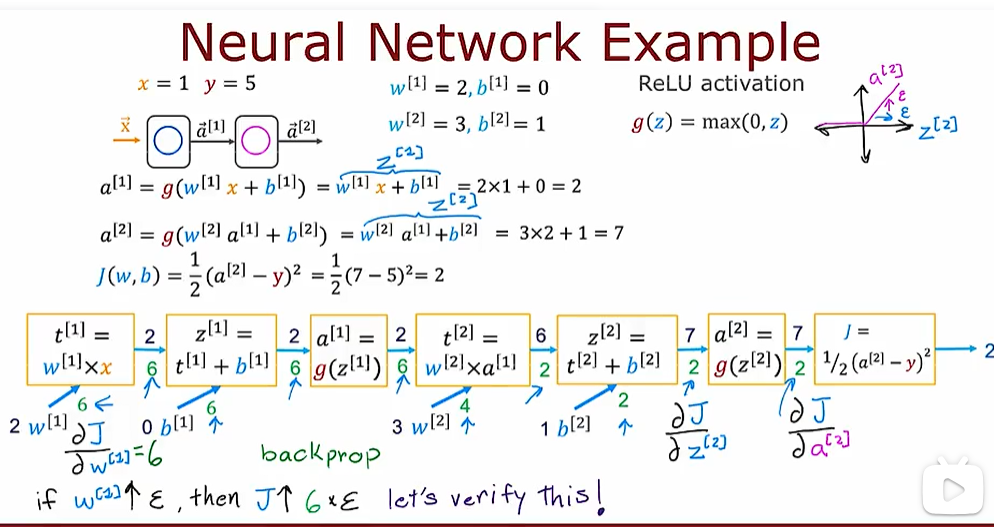
week3
1.1 决定下一步做什么

1.2 模型评估
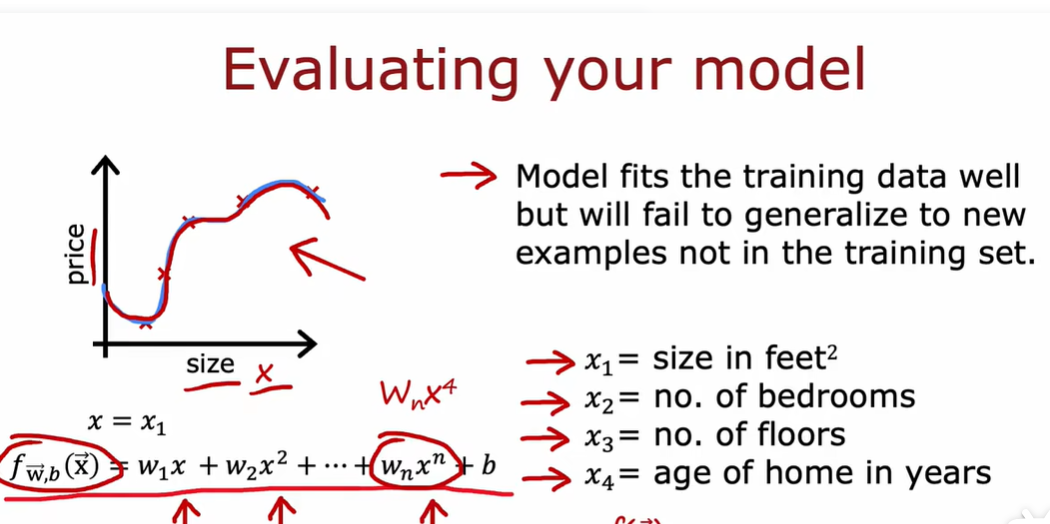
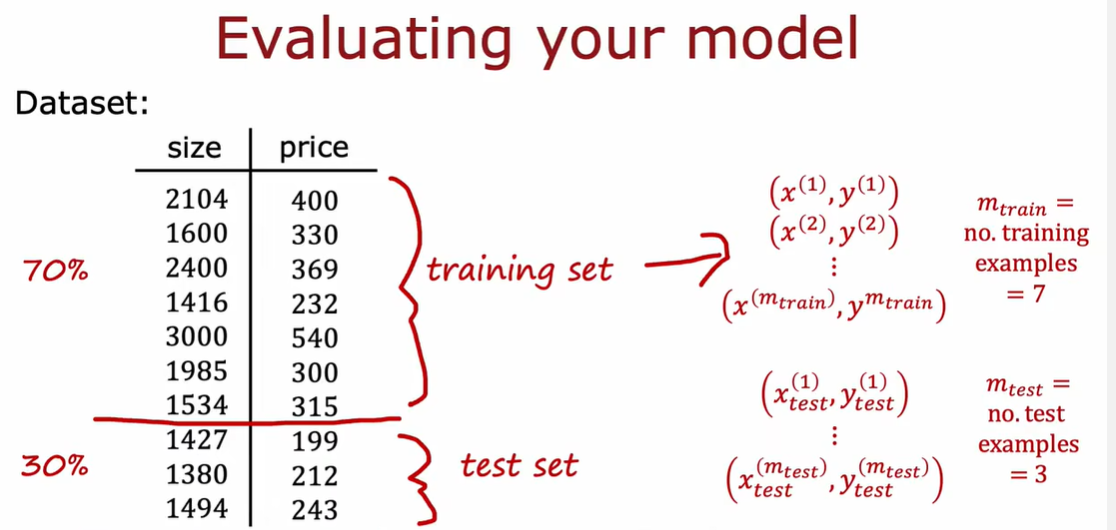
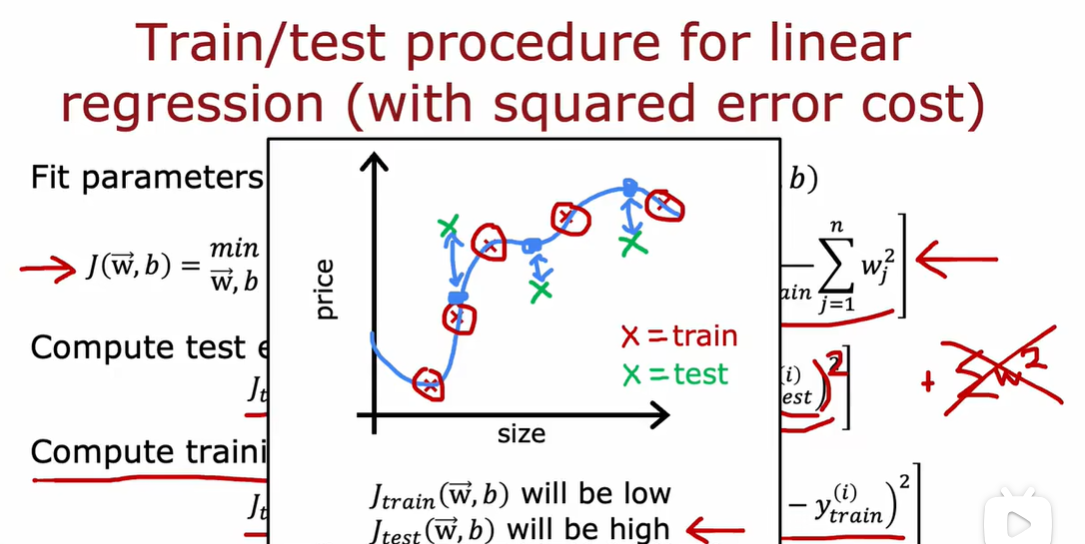

1.3 模型选择和交叉验证测试集的训练方法





因为选择d的过程是依赖于测试集数据的,这个d值可能恰好只是对于测试集来说的最优,但如果再用这个模型在测试集上评估性能,就不准确了
用验证集确定最优权重和阈值,用测试集确定最优模型类型
也就是,在训练集训练出d1到d10,十个模型;在交叉验证集上根据j值选择最小的那个模型;然后再测试集考察他的泛化能力;
测试集用过之后你不能去改模型,测试集本来就是评估模型的泛化能力的
训练集用于模型的学习和参数 w j调整;交叉验证集用于模型选择,例如调整超参数,(如决策树的树深)选择最佳模型;测试集用于最终评估模型性能
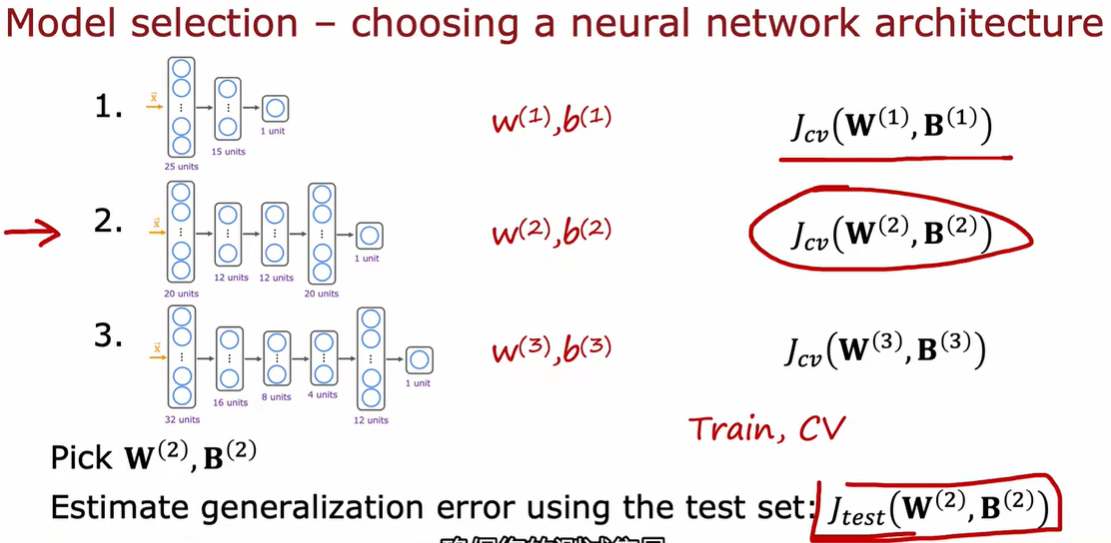
2.1 通过偏差和方法进行判断
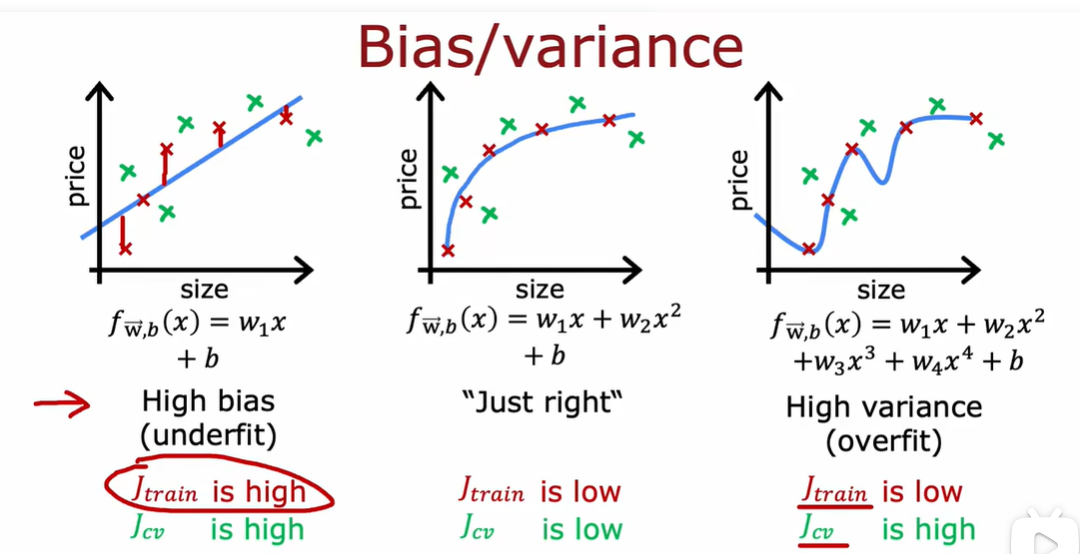
J_train不高说明没有高偏差问题,J_cv不比J_train差,说明没有高方差问题。

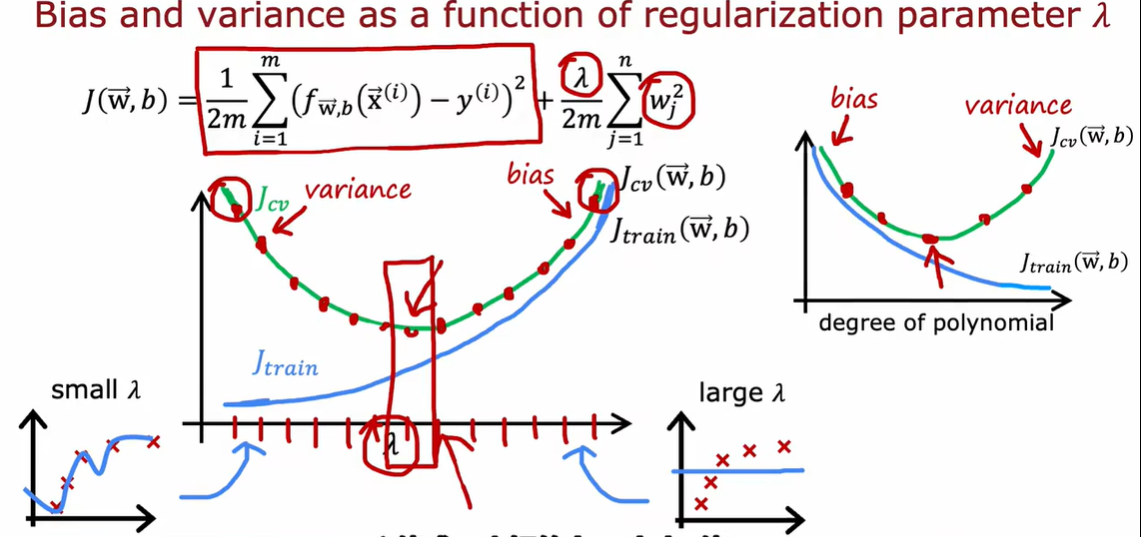
2.2 正则化、偏差、方差
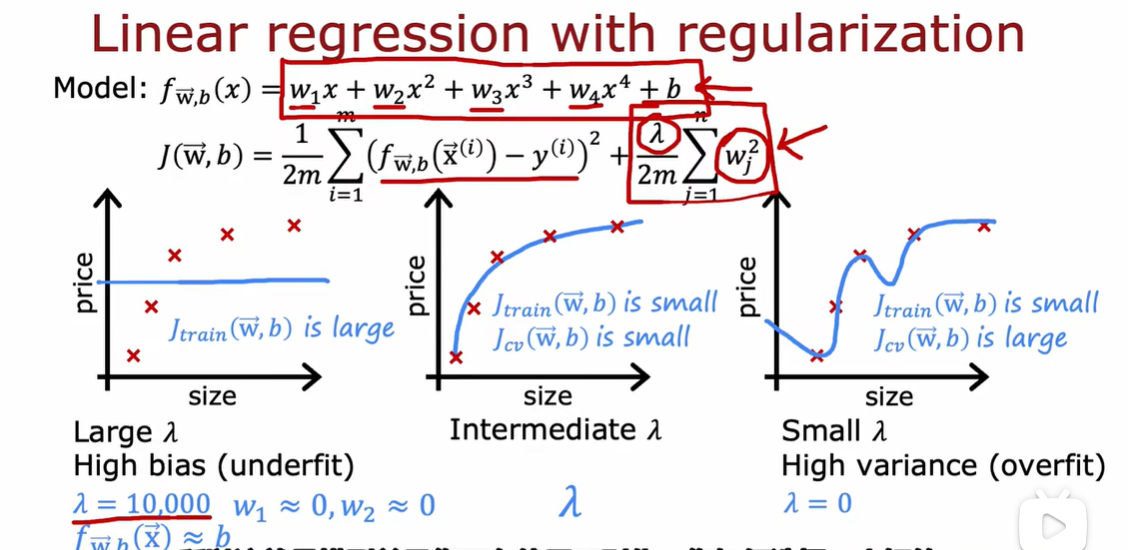
如何选择λ
最小化成本函数得到w1 b1,然后可以计算交叉验证误差

2.3 制定一个用于性能评估的基准



2.4 学习曲线
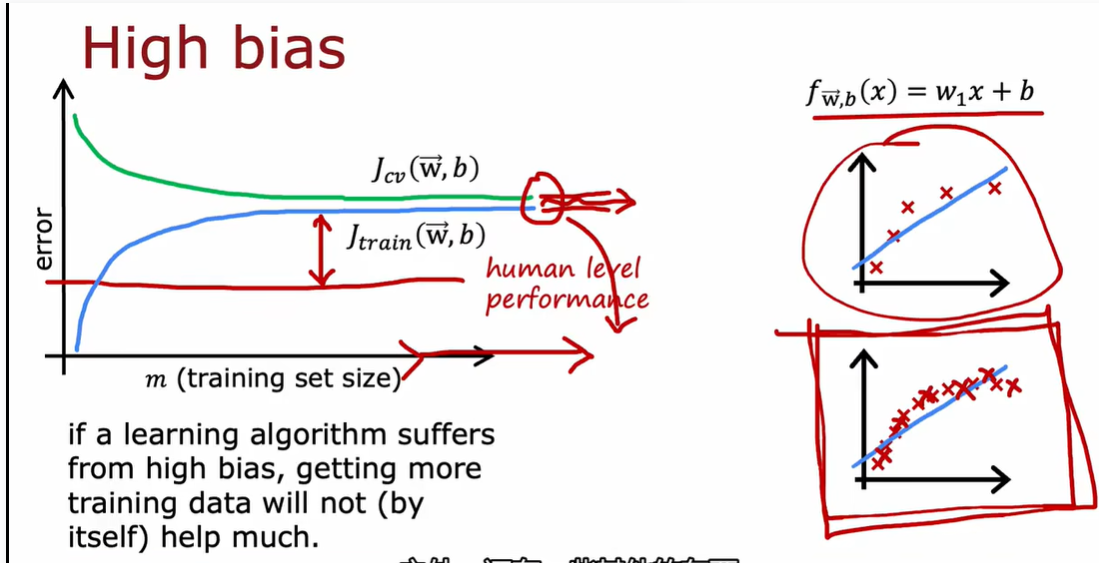
高偏差是欠拟合,模型能力不够,所以增加再多数据也没有用
高方差理解为过拟合,也就是模型能力强,数据少 所以增加数据量有用
简单来说就是增加training样本量可以减少variance,但对减少bias没作用
2.5下一步
high bias:获取尽量多的特征,添加尽量多的多项式特征,降低λ
high variance:获得尽量多的训练数据、尽量少的特征集合,提高λ
增加λ会迫使算法适应更加平滑的函数
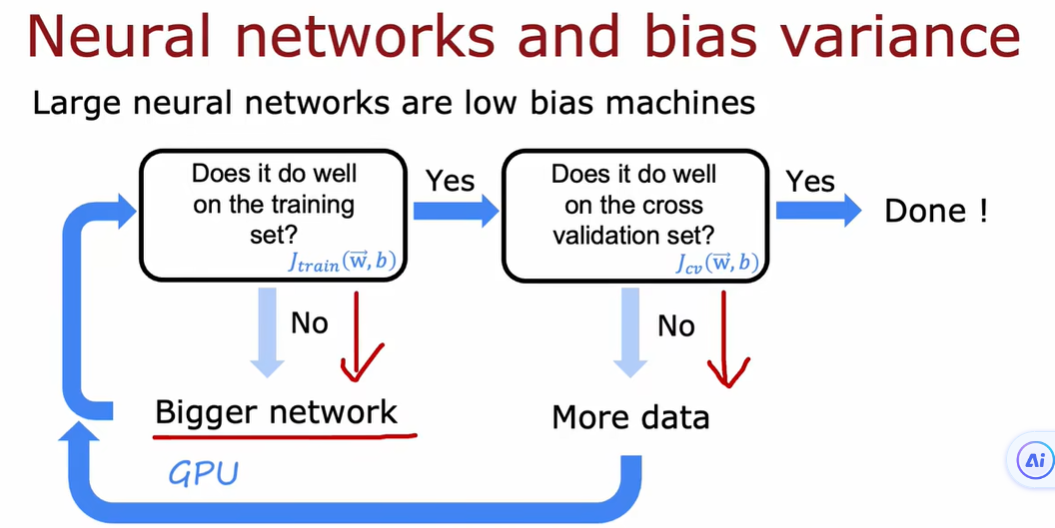
2.6 方差和偏差

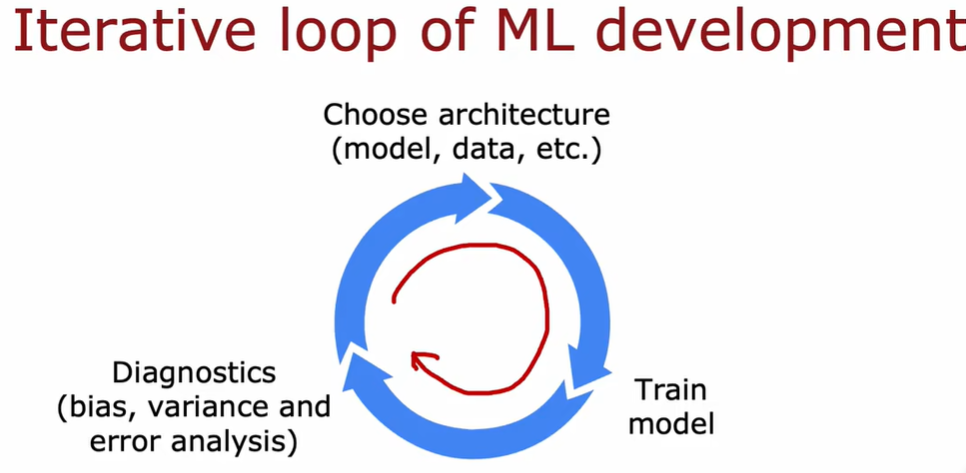
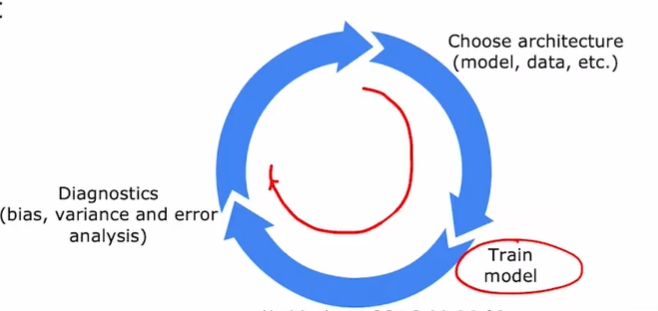
3.1 机器学习开发的迭代


3.2 误差分析

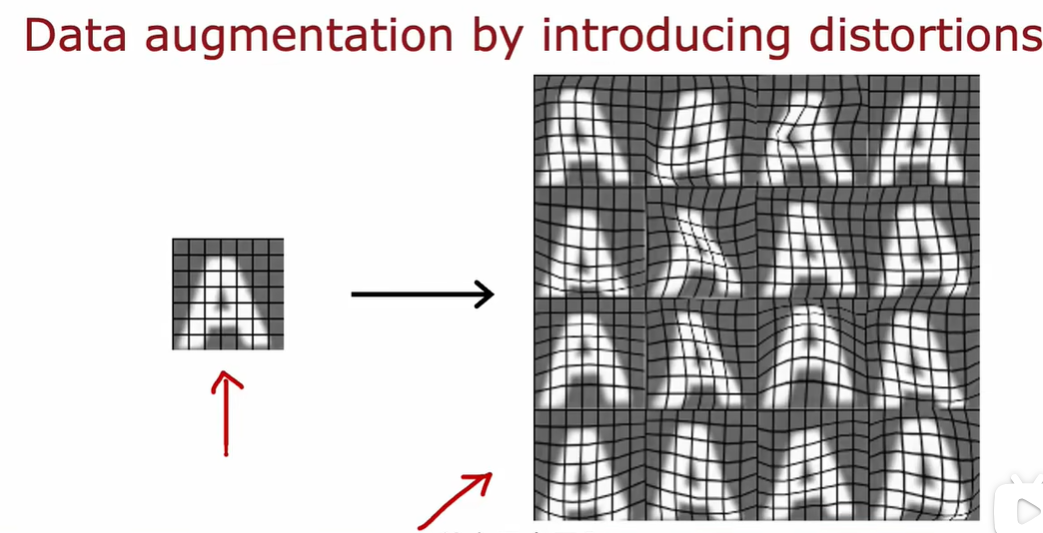
3.3 添加更多数据




3.4 迁移学习-使用其他任务中的数据
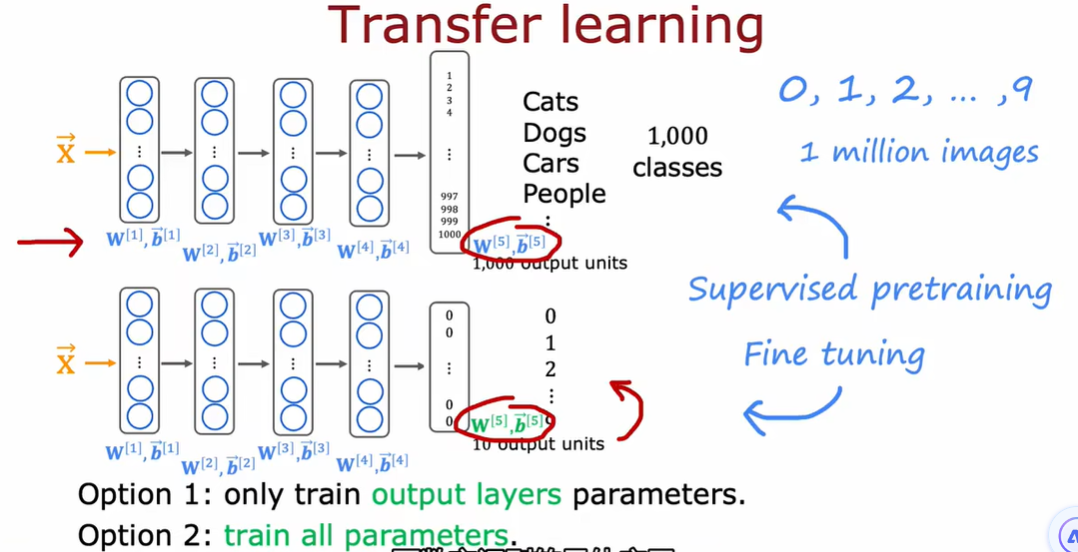
因为两个网络的本质都是图像分类,所以在隐藏层的大部分工作都是相似甚至一样的,所以直接把第一个网络的隐藏层拿过来用,对输出层重新训练就能实现新的功能。相当于螺丝刀的刀柄都是一样的,但把十字刀刀头换成一字刀作用就不一样了
如果训练集小,option1
如果训练集稍大,option2
图像处理的早期是有一些共性的,所以可以借用参数
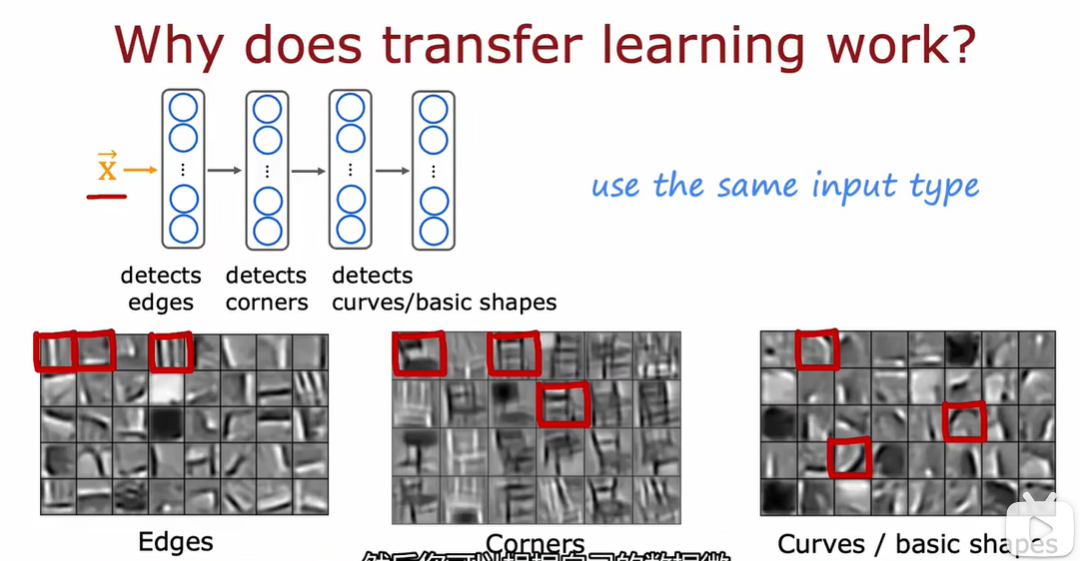

3.5 机器学习项目的完整周期
3.6 公平 偏见与伦理

4.1倾斜数据集的误差指标


准确率(Precision
精确率:在预测结果中有多少是正类
通过误差率可能并不能选择出最好的算法,因为这个误差小的可能不是特别有用的预测。
在这种量(比如某种疾病的患病率1%)比较少的数据集上,我们不仅用err rate来判断这个算法的表现如何
召回率 Recall
召回率:在所有正类中有多少是没被遗漏的
召回率可以帮助检测学习算法是否始终预测为0,如果你的算法只打印y=0,那么true positive将永远为0,因为永远不会预测positive
precision 一个预测pos里真的pos占比
recall 一个真的pos里预测pos占比
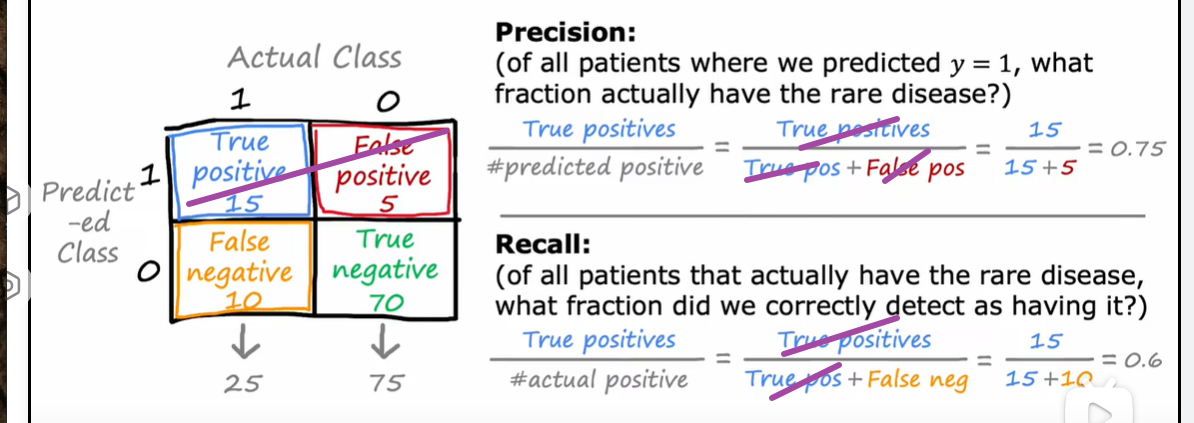
如果一直预测为0,没有true positive ,那么两者的分子都将为0
如果一个算法为0 precision或者0 recall都不是一个有用的算法,如果一个算法总是预测为0,那么他的precision 是undefined,因为是0/0
4.2 精确率和召回率的权衡
在理想情况下我们喜欢具有高精度和高召回率的算法,但在实际上,我们需要权衡准确率和召回率
高threshold :高准确率, 低召回率
低threshold:低准确率,高召回率
绘制不同阈值的精确率和召回率,可以让我们选择所需要的点

如果想自动权衡精确度和召回率,使用F1 score
将召回率和准确度合并为一个分数,F1只需查看哪个分数最高

F1 score是一种强调 precision and recall中比较低的值,因为事实证明,如果算法的精度和召回率非常低,说明二者没有那么有用。F1 score是一种计算平均分数的方法,更加关注较低的分数
F1 score是一种均值,调和均值是一种更强调较小值的平均值
week 4
1.1 决策树模型
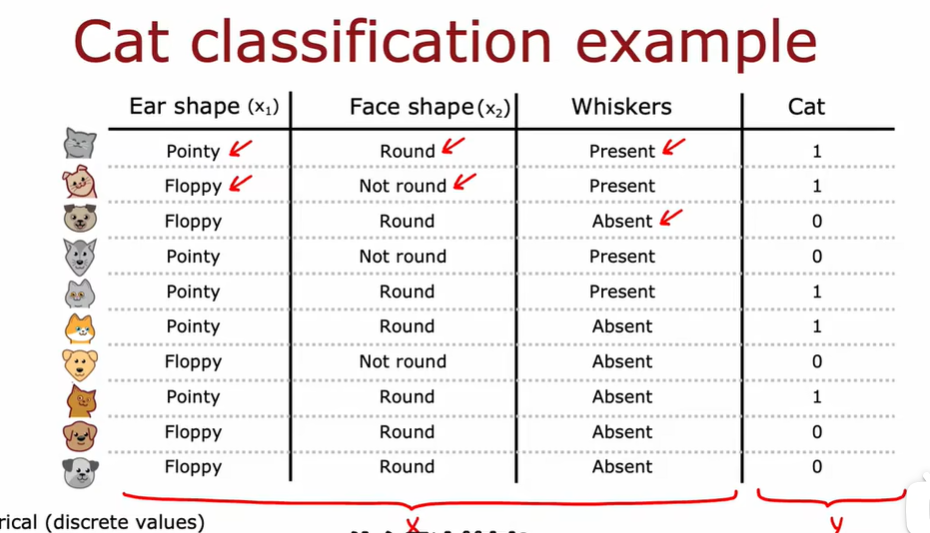
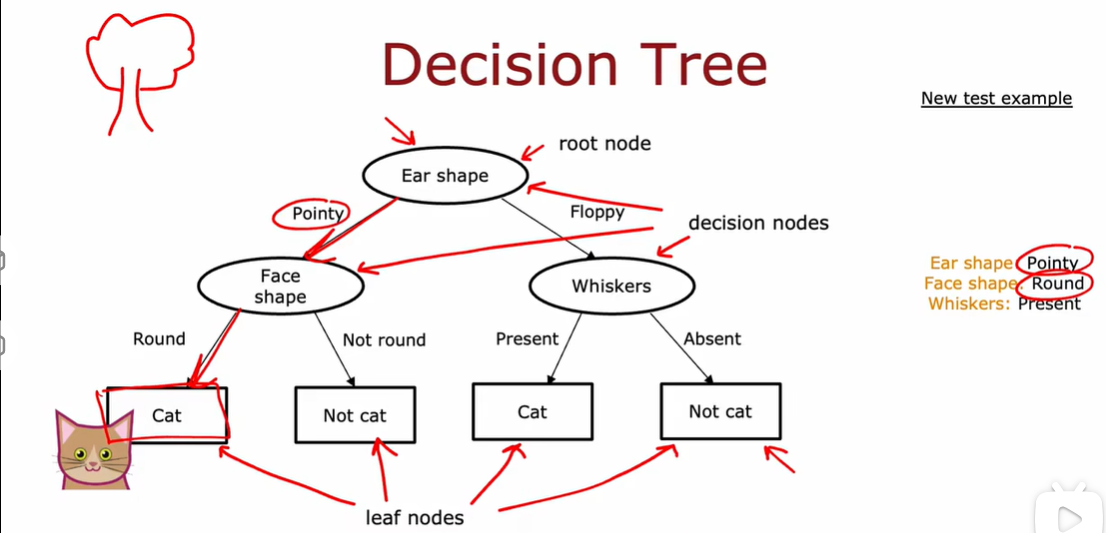
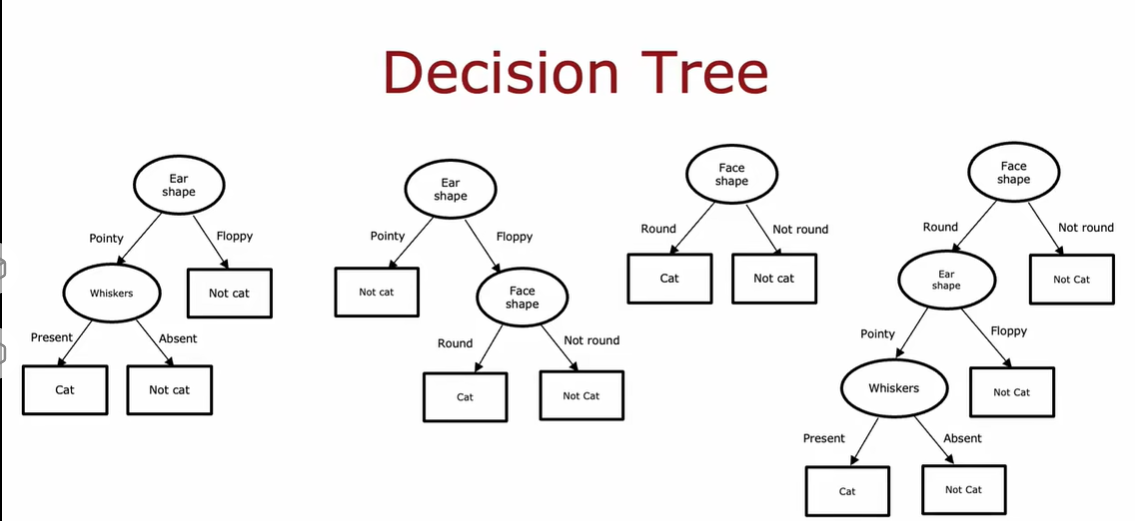
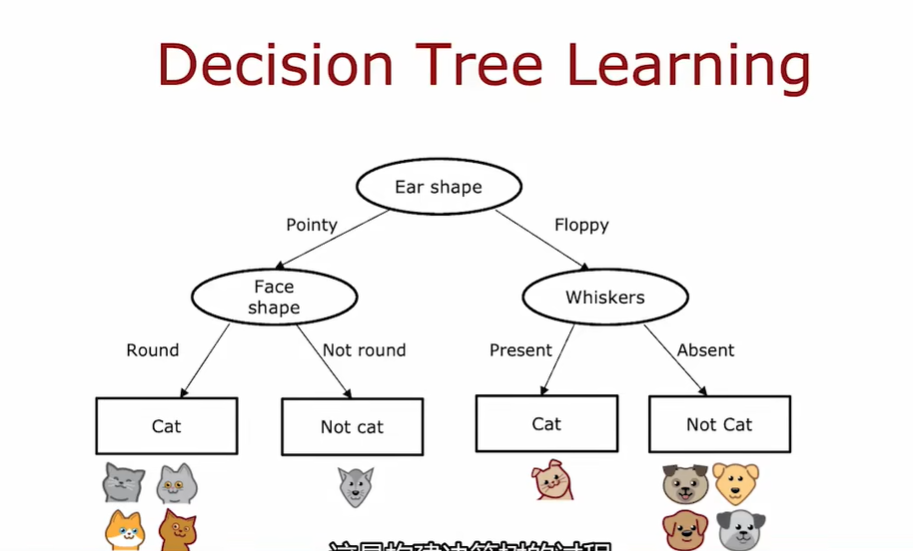
1.2 学习过程
floppy 下垂的耳朵
pointy 尖耳朵
构建决策树的第一个关键点:选择哪一个特征来划分每个节点
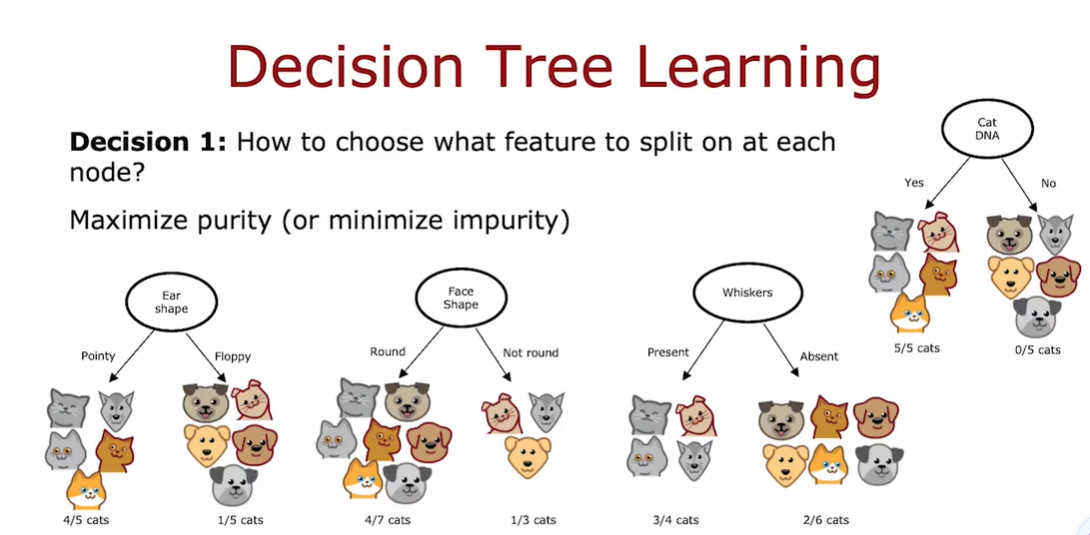
构建决策树的第二个关键点:什么时候停止划分
- 当节点获得了100%的分类结果(When a node is 100% one class);
- 当划分节点会导致超过树的最大深度(When splitting a node will result in the tree exceeding a maximum depth);
- 当纯度值的增长低于一定阈值(When improvements in purity score are below a threshold);
- 当节点中案例数量低于一定阈值(When number of examples in a node is below a threshold)。
2.1 纯度
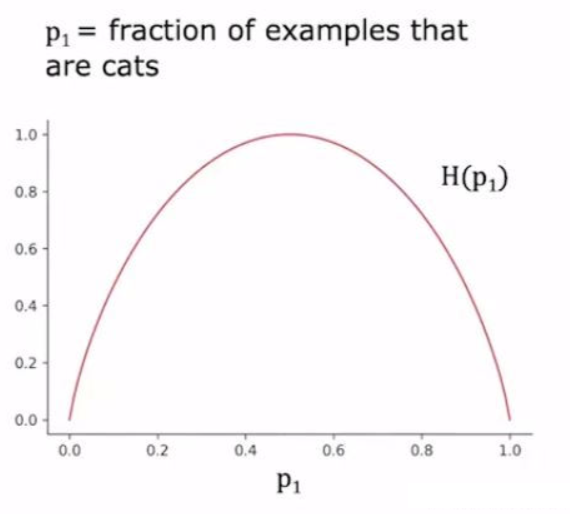
熵:衡量一组数据不纯程度的指标(Entropy as a measure of impurity)

如图,p1指代一组分类结果中猫的占比(剩下的是狗);H(p1)是熵;图中为熵与p1的关系;可见熵随着纯度的增大呈现先增大后减小的趋势;在p1=0.5时(如,3个猫3个狗)熵达到最大值1,在p1分别为0(6个狗)和1(6个猫)两个端点时,熵最小,值为0。
图中熵函数的公式:
首先定义集合中除了猫之外的小动物占比:
熵函数:
也可以记为:
为了计算,这里设定:
\[0log_{2}(0) = 0 \]选用2为底数而非e或者10,是为了让极大值为1,换成其它底数相当于现有函数图像上下等比例伸缩。
Gini函数也可以用作熵函数,但本课简单起见使用这里介绍的entropy criteria函数。
2.2 选择拆分信息增益
信息增益(information gain):衡量从上一节点分裂出两个节点后,这种分裂方法对应的熵的减少量(the reduction in entropy that you get in your tree resulting from making a split)。
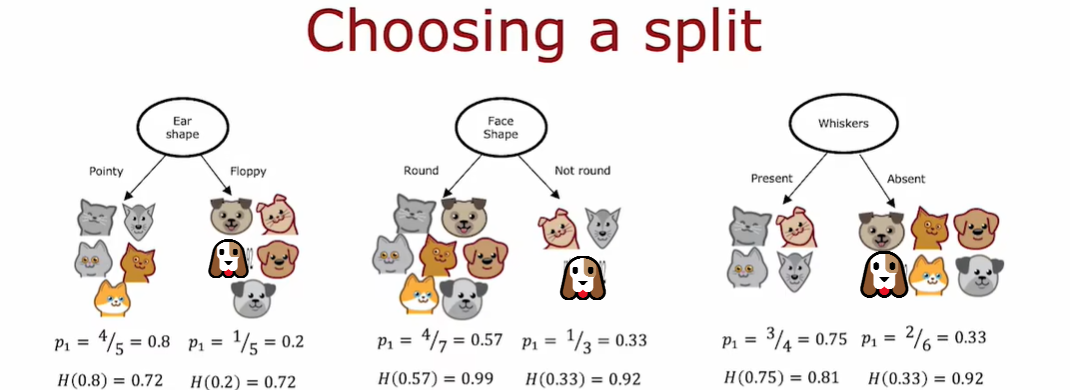
如果一个节点中有比较多的实例并且具有高熵,这比有一个节点中只有几个实例具有高熵更加糟糕。因为熵作为杂质的度量,如果你有一个非常大而且不纯的数据集,那么比只有几个例子和不纯的树的一个分支相比,熵会更加糟糕

在根节点的使用上,在这三种可能的特征选择上,我们需要使用哪一种?
使用加权平均,在左右两个子分支中,低熵还需要取决于这里左右节点的实例。我们这里计算的是熵的减少,而不知是左右子分支的熵。
熵最初在根节点处是 1,通过拆分得到比较低的熵值,这两个值之间的差异是熵的减少。决定何时不再进行分裂的停止标准之一是熵的减少是否太小。这里我们选择用ear shape作为根节点来划分,因为根节点这里的熵减少的最多。

信息增益的计算公式:
w_left 和 w_right:这两个分别是左子节点和右子节点的权重,通常等于它们各自包含的样本数量占总样本数量的比例。
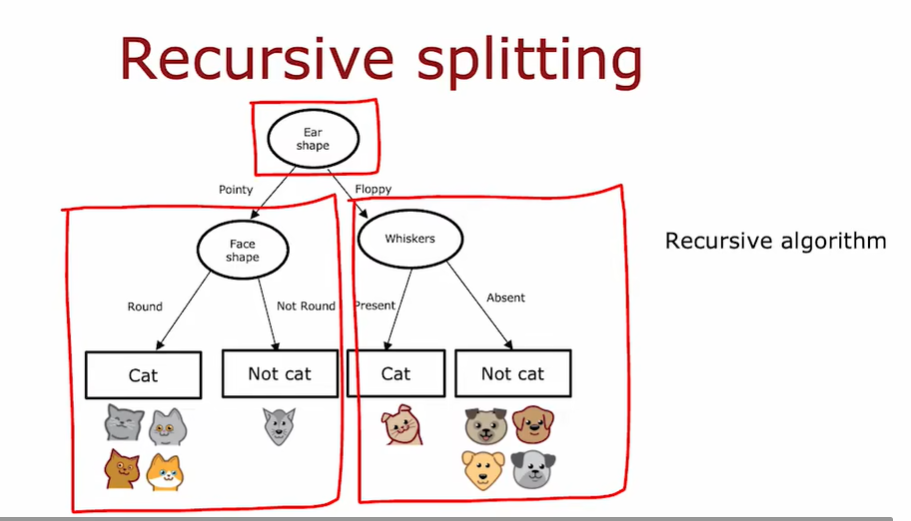
2.3 整合
决策树的计算过程:
- 从树的根节点的所有训练实例开始
- 计算所有特征的信息增益,选择要拆分的特征,提供最高的信息增益
- 根据所选择的特征将数据集拆分为两个子集,并创建树的左右分支,并将训练实例分到左右两侧
- 重复划分直至达到了停止分裂的准则
- When a node is 100% one class
- When splitting a node will result in the tree exceeding a maximum depth
- Information gain from additional splits is less than threshold
- When number of examples in a node is below a threshold
2.4 独热编码 One-hot
现在构建了三个新特征,而不是一个特征采用三个可能的值。这里每个特征智能采用两个可能值中的一个1或者0
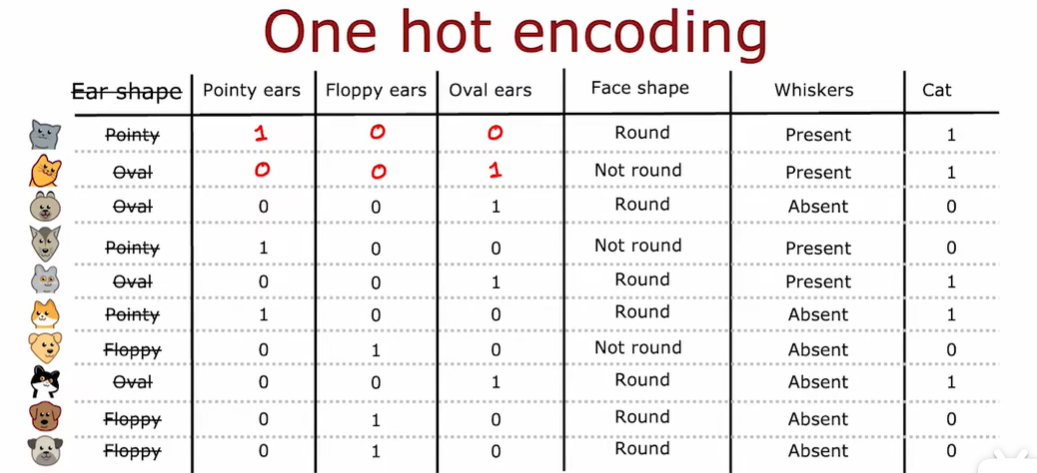
如果一个特征可以取k个可能的值,那么在我的例子中k是三个,那么我们将通过创建k个只能取值0或者1的二进制变量来取代他
在这三个特征中,一定有一个恰好为1,这就是为什么称为one-hot的原因。
采用one-hot编码,可以让决策树采用两个以上的离散值特征,也可以将其应用于新的网络或者线性回归或者逻辑回归训练。
2.5 连续有价值的功能
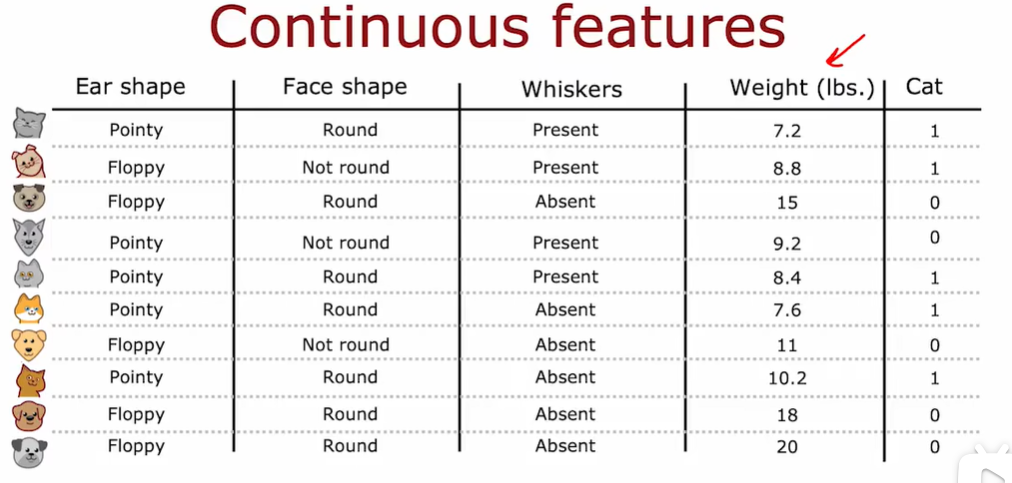
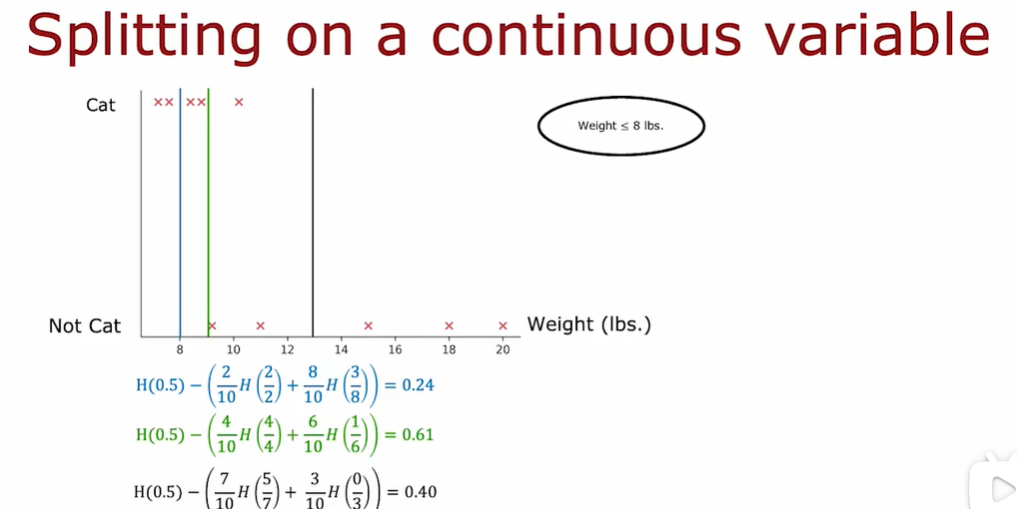
当对权重特征进行约束拆分的时候,我们应该考虑这个阈值的不同的值,选择能够带来最好的信息增益的那个。
2.6 回归树
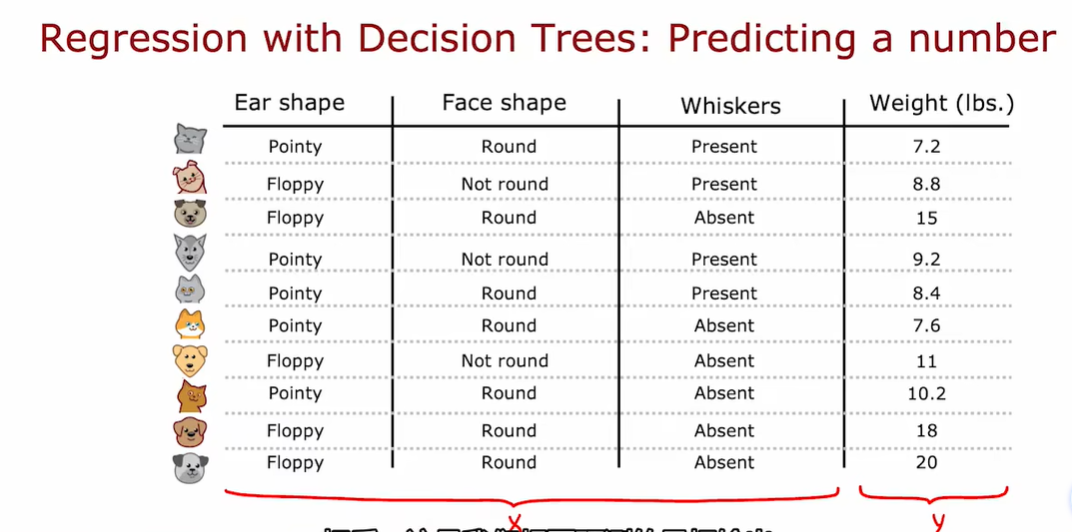
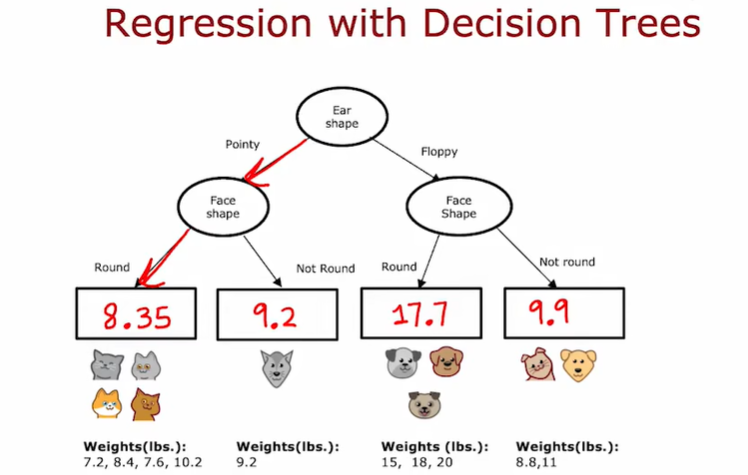
这里的加权平均方差和我们决定使用什么分割时候用的加权平均熵,有着非常相似的作用

选择最小的加权方差
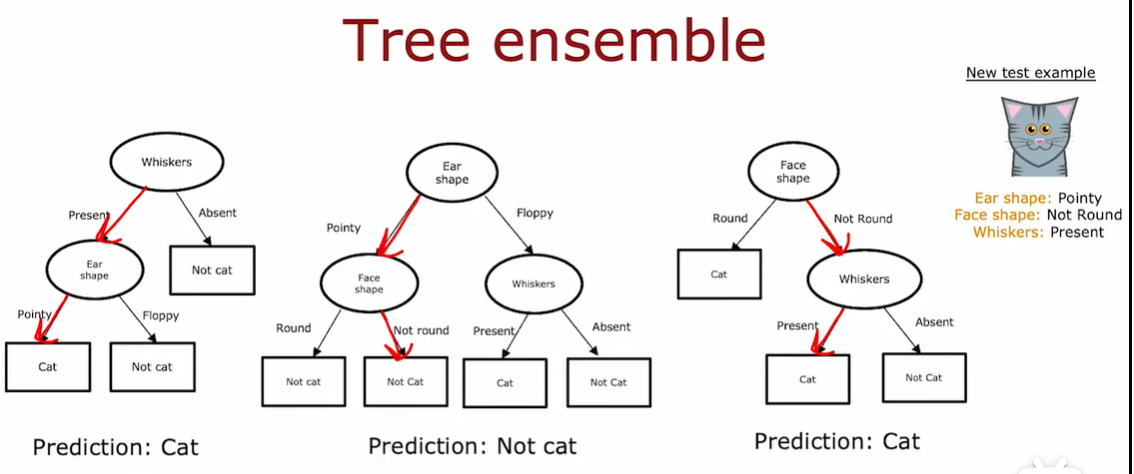
3.1 使用多个决策树
使用单一决策树可能会对数据中的微小变化高度敏感。
 仅改变一个训练实例就会导致算法的决策树不同
仅改变一个训练实例就会导致算法的决策树不同
3.2 有放回取样
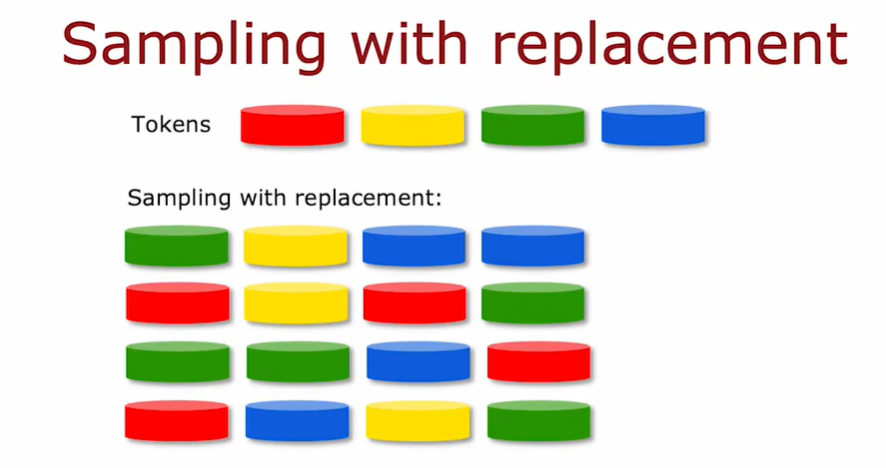
构建多个随机训练集,这些训练集都与我们原始的训练集略有不同
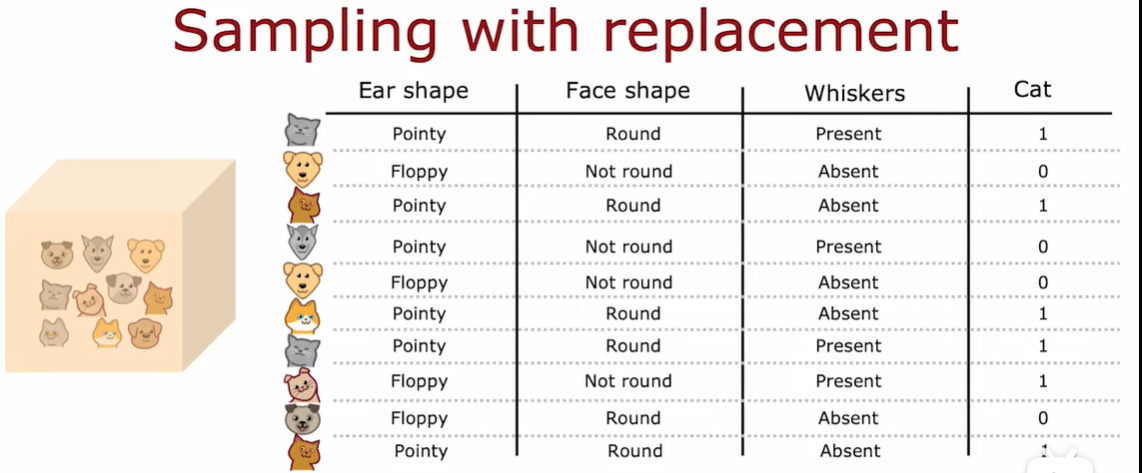
意义就是 好几个 决策树使用的训练样本都不太一样 但是又都是属于原来的训练样本
3.3 随机森林



where does a machine learning engineer go camping? In a random forest
3.4 XGBoost
决策树最常用的一种方式
抽样的时候不是从m个等概率样本中选择1/m的概率,而是让我们更有可能选择先前训练的树表现不佳的错误分类样本

第四列是预测,根据分类是否正确进行打勾
第二次循环需要做的是,把这些错误的放到十个实例中,当每次选择的时候,都有更高的机会从这三个仍然错误的分类实例中选择一个。
今天使用最广泛的一种实现Boost的就是XGBoost
- 开源
- 高效
- 很好的默认拆分标准和何时选择停止拆分的标准
- 内置了正则化防止过度拟合


3.5 何时使用决策树
决策树和神经网络都是非常强大的学习算法,如何选择
Tree ensembles:
优点:
- 表格(结构化)数据
- Fast
- 小型的决策树可以是人类可以解释的,可以方便打印查看
缺点:
- 比单个决策树更加昂贵,计算预算有限,可能会使用单个决策树
Neural Networks:
优点:
- 所有种类的数据,包括结构的和非结构化数据(照片,视频,文本)等
- 可以和迁移学习一起使用
缺点:
- 慢,需要很长时间来训练
- 可以和迁移算法一起
- 可以和多个模型一起工作,这可能很容易将多个神经网络串起来
如果你的模型 需要很多小时来训练会限制完成循环并提升算法性能的速度,但由于决策树的训练速度往往非常快,因此可以更快的进入此循环,并且可能更有效的提升学习算法 的性能。
May the force be with you


 浙公网安备 33010602011771号
浙公网安备 33010602011771号